金融原理/第 1 部分/第 7 章/現代投資組合理論

現代投資組合理論（MPT）是一種金融理論，它試圖透過仔細選擇各種資產的比例來最大化給定投資組合風險的投資組合預期收益，或者等效地最小化給定預期收益水平的風險。 雖然 MPT 在金融行業被廣泛使用，並且它的幾位創立者因該理論獲得了諾貝爾經濟學獎， 但近年來，行為經濟學等領域的學者對 MPT 的基本假設提出了廣泛的質疑。

MPT 是投資多元化概念的數學表達形式，其目標是選擇一個投資資產組合，該組合的整體風險低於任何單個資產。直觀地可以看出，這是可能的，因為不同型別的資產價格變化往往是相反的。 例如，在一定程度上，股票市場的價格與債券市場的價格變化不同，因此，理論上，包含這兩種型別資產的集合可以承受比任何單獨資產都低的總體風險。但即使資產的回報不呈負相關，多元化也能降低風險——事實上，即使它們呈正相關也是如此。

更準確地說，MPT 將資產的回報建模為正態分佈函式（或更一般地，為橢圓分佈隨機變數），將風險定義為回報的標準差，並將投資組合建模為資產的加權組合，因此，投資組合的回報是資產回報的加權組合。透過組合回報不完全正相關的不同資產，MPT 試圖降低投資組合回報的總方差。MPT 還假設投資者是理性的，市場是有效的。

MPT 在 1950 年代至 1970 年代初發展起來，被認為是金融數學建模領域的一項重大進展。從那時起，它受到了許多理論和實踐上的批評。這些批評包括：金融回報不遵循高斯分佈，也不遵循任何對稱分佈；資產類別之間的相關性並非固定，而是會根據外部事件（尤其是在危機時期）而變化。此外，越來越多的證據表明，投資者並不理性，市場並不有效。

概念

MPT 背後的基本概念是，投資組合中的資產不應單獨選擇，每個資產都具有自己的優點。相反，重要的是要考慮每個資產的價格變化相對於投資組合中所有其他資產的價格變化。

投資是風險和預期回報之間的權衡。一般來說，預期回報更高的資產風險更大。對於給定的風險量，MPT 描述瞭如何選擇預期回報最高的投資組合。或者，對於給定的預期回報，MPT 解釋瞭如何選擇風險最低的投資組合（目標預期回報當然不能超過可投資的最高回報證券，除非可以進行負資產持倉）。

因此，MPT 是一種多元化形式。在某些假設下，對於風險和回報的特定量化定義，MPT 解釋瞭如何找到最佳的多元化策略。

歷史

Harry Markowitz 在 1952 年的一篇文章 和 1959 年的一本書中介紹了 MPT。 Markowitz 稱之為“投資組合理論”，因為“它本身並不現代”。另請參見此 歷史調查。

數學模型

在某種意義上，下面推導的數學公式就是MPT，儘管模型背後的基本概念也很有影響力。

本節介紹“經典”的 MPT 模型。此後，該模型進行了許多擴充套件。

風險和預期收益

MPT 假設投資者是風險厭惡的，這意味著給定兩個提供相同預期回報的投資組合，投資者會選擇風險較小的那個。因此，投資者只有在獲得更高的預期回報時才會承擔更高的風險。反之，想要獲得更高預期回報的投資者必須接受更高的風險。所有投資者的精確權衡都是一樣的，但不同的投資者會根據個人風險厭惡特徵對權衡進行不同的評估。這意味著，理性的投資者不會投資於一個投資組合，如果存在另一個投資組合具有更優的風險-預期回報特徵——也就是說，對於該風險水平，存在一個具有更好預期回報的替代投資組合。

請注意，該理論使用回報的標準差來代替風險，這在資產回報是聯合正態分佈或其他橢圓分佈的情況下是有效的。然而，這方面存在問題；請參閱批評部分。

在該模型下

• 投資組合回報是組成資產回報的比例加權組合。
• 投資組合波動率是組成資產相關性ρ_ij的函式，對於所有資產對 (i, j) 來說都是如此。

一般來說

• 預期回報

$\operatorname {E} (R_{p})=\sum _{i}w_{i}\operatorname {E} (R_{i})\quad$

其中 $R_{p}$ 是投資組合的收益率，$R_{i}$ 是資產 i 的收益率，$w_{i}$ 是構成資產 $i$ 的權重（即資產 i 在投資組合中的比例）。

• 投資組合收益率方差

$\sigma _{p}^{2}=\sum _{i}w_{i}^{2}\sigma _{i}^{2}+\sum _{i}\sum _{j\neq i}w_{i}w_{j}\sigma _{i}\sigma _{j}\rho _{ij},$

其中 $\rho _{ij}$ 是資產 i 和 j 收益率之間的相關係數。或者，表示式可以寫成

$\sigma _{p}^{2}=\sum _{i}\sum _{j}w_{i}w_{j}\sigma _{i}\sigma _{j}\rho _{ij}$,

其中 $\rho _{ij}=1$ 當 i=j 時。

• 投資組合收益率波動率（標準差）

$\sigma _{p}={\sqrt {\sigma _{p}^{2}}}$

對於一個包含兩種資產的投資組合

• 投資組合收益率：$\operatorname {E} (R_{p})=w_{A}\operatorname {E} (R_{A})+w_{B}\operatorname {E} (R_{B})=w_{A}\operatorname {E} (R_{A})+(1-w_{A})\operatorname {E} (R_{B}).$
• 投資組合方差：$\sigma _{p}^{2}=w_{A}^{2}\sigma _{A}^{2}+w_{B}^{2}\sigma _{B}^{2}+2w_{A}w_{B}\sigma _{A}\sigma _{B}\rho _{AB}$

對於一個包含三種資產的投資組合

• 投資組合收益率：$w_{A}\operatorname {E} (R_{A})+w_{B}\operatorname {E} (R_{B})+w_{C}\operatorname {E} (R_{C})$
• 投資組合方差: $\sigma _{p}^{2}=w_{A}^{2}\sigma _{A}^{2}+w_{B}^{2}\sigma _{B}^{2}+w_{C}^{2}\sigma _{C}^{2}+2w_{A}w_{B}\sigma _{A}\sigma _{B}\rho _{AB}+2w_{A}w_{C}\sigma _{A}\sigma _{C}\rho _{AC}+2w_{B}w_{C}\sigma _{B}\sigma _{C}\rho _{BC}$

多元化

投資者可以透過持有不完全正相關（相關係數 $-1\leq \rho _{ij}<1$）的組合工具來降低投資組合風險。換句話說，投資者可以透過持有多元化的資產組合來降低其對單個資產風險的敞口。多元化可能允許在降低風險的情況下獲得相同的投資組合預期收益。這些想法最初是由馬科維茨提出的，後來得到了其他經濟學家和數學家（如安德魯·布倫南）的認可，他們在投資組合理論中表達了透過多元化減少方差的想法。

如果所有資產對的相關性都為 0——它們完全不相關——那麼投資組合的收益方差是所有資產的收益方差平方與該資產持有比例平方的總和（投資組合標準差是該總和的平方根）。

沒有無風險資產的有效邊界

有效邊界。雙曲線有時被稱為“馬科維茨子彈”，如果不存在無風險資產，則是有效邊界。如果存在無風險資產，則直線是有效邊界。

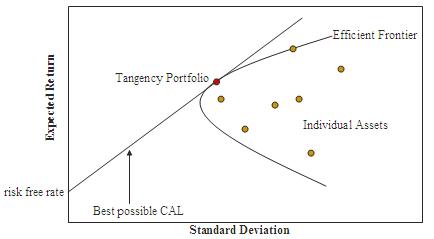
如該圖所示，不包括任何無風險資產的任何可能的風險資產組合，都可以在風險-預期收益空間中繪製，所有這些可能組合的集合定義了該空間中的一個區域。該區域的左邊界是雙曲線， 該區域的上邊緣是在沒有無風險資產的情況下（有時被稱為“馬科維茨子彈”）的有效邊界。沿著該上邊緣的組合代表投資組合（包括沒有無風險資產的持有），這些投資組合在給定預期收益水平下具有最低風險。等效地，位於有效邊界上的投資組合代表在給定風險水平下提供最佳可能預期收益的組合。

矩陣更適合計算有效邊界。

以矩陣形式，對於給定的“風險承受能力” $q\in [0,\infty )$，有效邊界可以透過最小化以下表達式找到

$w^{T}\Sigma w-q*R^{T}w$

其中

• $w$ 是投資組合權重的向量，並且 $\sum _{i}w_{i}=1.$（權重可以為負，這意味著投資者可以賣空證券）；
• $\Sigma$ 是投資組合中資產收益的協方差矩陣；
• $q\geq 0$ 是一個“風險承受能力”因子，其中 0 會導致風險最小的投資組合，而 $\infty$ 會導致投資組合無限地延伸到邊界，預期收益和風險都無界；以及
• $R$ 是預期收益的向量。
• $w^{T}\Sigma w$ 是投資組合收益的方差。
• $R^{T}w$ 是投資組合的預期收益。

上述最佳化找到了邊界上的一個點，在這個點上，如果投資組合收益方差而不是標準差在水平方向上繪製，則邊界的斜率的倒數將是q。邊界整體上是關於q引數化的。

許多軟體包（包括 MATLAB、Microsoft Excel、Mathematica 和 R）都提供適合上述問題的最佳化例程。

確定有效邊界的一種替代方法是按預期投資組合收益$R^{T}w.$進行引數化。這種問題的版本要求我們最小化

$w^{T}\Sigma w$

受制於

$R^{T}w=\mu$

引數$\mu$。這個問題可以使用拉格朗日乘子輕鬆解決。

兩個共同基金定理

上述分析的一個關鍵結果是兩個共同基金定理。 該定理指出，有效邊界上的任何投資組合都可以透過持有邊界上任意兩個給定投資組合的組合來生成；後兩個給定投資組合是定理名稱中的“共同基金”。因此，在沒有無風險資產的情況下，即使投資者只能獲得一對有效共同基金，也可以實現任何所需的有效投資組合。如果所需投資組合在有效邊界上的位置位於兩個共同基金位置之間，則將以正量持有這兩個共同基金。如果所需投資組合位於兩個共同基金跨越的範圍之外，則必須賣空其中一個共同基金（以負量持有），而對另一個共同基金的投資規模必須大於可供投資的金額（超出部分由從另一個基金借款提供資金）。

無風險資產和資本配置線

無風險資產是（假設的）資產，它支付無風險利率。在實踐中，短期政府債券（例如美國國庫券）被用作無風險資產，因為它們支付固定利率，並且違約風險極低。無風險資產的收益方差為零（因此是無風險的）；它也與任何其他資產不相關（根據定義，因為它的方差為零）。因此，當它與任何其他資產或資產組合組合時，當組合中的比例發生變化時，收益的變化與風險的變化呈線性關係。

當引入無風險資產時，圖中所示的半直線是新的有效邊界。它在具有最高夏普比率的純風險投資組合處與雙曲線相切。它的水平截距表示一個投資組合，其 100% 的持倉為無風險資產；與雙曲線的切線表示一個投資組合，其無風險持倉為 0%，所有資產都持有發生在切點處的投資組合；這些點之間的點是包含正量風險切線投資組合和無風險資產的投資組合；半直線超出切點處的點是槓桿投資組合，涉及無風險資產的負持倉（後者被賣空——換句話說，投資者以無風險利率借款），並且投資於切線投資組合的金額超過投資者的初始資金的 100%。這個有效的半直線被稱為資本配置線 (CAL)，它的公式可以證明為

$E(R_{C})=R_{F}+\sigma _{C}{\frac {E(R_{P})-R_{F}}{\sigma _{P}}}.$

在這個公式中，P 是與馬科維茨彈丸相切的風險資產子投資組合，F 是無風險資產，C 是投資組合 P 和 F 的組合。

從圖中可以看出，將無風險資產引入作為投資組合可能組成部分，提高了可用風險-預期收益組合的範圍，因為除了切線投資組合以外，半直線在每個可能的風險水平上都比雙曲線提供更高的預期收益。所有線性有效軌跡上的點都可以透過持有無風險資產和切線投資組合的組合來實現，這一事實被稱為一個共同基金定理。，其中提到的共同基金是切線投資組合。

使用 MPT 進行資產定價

上述分析描述了個人投資者的最優行為。資產定價理論以如下方式建立在這個分析的基礎上。由於每個人都以相同比例持有風險資產——即切線投資組合中給出的比例——在市場均衡狀態下，風險資產的價格，因此它們的預期收益將進行調整，以使切線投資組合中的比率與風險資產供應給市場的比率相同。因此，相對供應將等於相對需求。MPT 在這種情況下推匯出正確定價資產的所需預期收益。

系統性風險和特有風險

特有風險與單個資產相關聯 - 在投資組合中，這些風險可以透過多元化來降低（特有風險“抵消”）。特有風險也稱為可分散風險、獨特風險、非系統性風險或特質風險。系統性風險（又名投資組合風險或市場風險）是指所有證券共有的風險——除了賣空外，系統性風險無法透過分散投資消除（在一個市場內）。在市場投資組合中，資產特有風險將在最大程度上透過分散投資消除。因此，系統性風險等同於市場投資組合的風險（標準差）。

由於只有當證券能夠改善市場投資組合的風險-預期收益特徵時，才會購買該證券，因此，衡量證券風險的適當指標是它新增到市場投資組合中的風險，而不是孤立的風險。在這種情況下，資產的波動性及其與市場投資組合的相關性是根據歷史觀察得出的，因此是已知的。（有幾種資產定價方法試圖透過對資產收益的矩的隨機屬性進行建模來對資產進行定價——這些方法通常被稱為條件資產定價模型。）

可以透過在單個投資組合中使用多頭和空頭頭寸的策略來管理一個市場中的系統性風險，從而建立一個“市場中性”投資組合。

資本資產定價模型

資產收益取決於今天支付的資產金額。支付的價格必須確保在將資產新增到市場組合時，市場組合的風險/收益特徵得到改善。CAPM 模型推匯出資產在市場中的理論必要預期收益（即折現率），該模型考慮了投資者可獲得的無風險利率以及整個市場的風險。CAPM 通常表示為

$\operatorname {E} (R_{i})=R_{f}+\beta _{i}(\operatorname {E} (R_{m})-R_{f})$

• $\beta$，即貝塔係數，是衡量資產對整體市場變動敏感程度的指標；貝塔係數通常透過對歷史資料的迴歸分析得出。貝塔係數大於 1 表示資產對整體投資組合風險的貢獻大於平均水平；貝塔係數小於 1 表示資產對整體投資組合風險的貢獻低於平均水平。

• $(\operatorname {E} (R_{m})-R_{f})$ 是市場溢價，即市場組合預期收益超過無風險利率的預期超額收益。

可以使用以下回歸方程對該方程進行統計估計

$\mathrm {SCL} :R_{i,t}-R_{f}=\alpha _{i}+\beta _{i}\,(R_{M,t}-R_{f})+\epsilon _{i,t}{\frac {}{}}$

其中 α_i 稱為資產的阿爾法，β_i 是資產的貝塔係數，SCL 是證券特徵線。

一旦使用 CAPM 計算出資產的預期收益，$E(R_{i})$，可以使用該比率將資產的未來現金流折現到現值，以確定資產的正確價格。風險較高的股票將具有較高的貝塔係數，並以較高的比率折現；風險敏感度較低的股票將具有較低的貝塔係數，並以較低的比率折現。理論上，當資產的觀察價格與其使用 CAPM 推匯出的折現率計算出的價值相同，則該資產的定價是合理的。如果觀察價格高於估值，則該資產被高估；如果價格過低，則被低估。

（1）在將額外的風險資產 a 新增到市場組合 m 中時，風險和預期收益的增量影響遵循雙資產投資組合的公式。這些結果用於推匯出適用於資產的折現率。

• 市場組合的風險 = $(w_{m}^{2}\sigma _{m}^{2}+[w_{a}^{2}\sigma _{a}^{2}+2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}])$

因此，新增到投資組合的風險 = $[w_{a}^{2}\sigma _{a}^{2}+2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]$

但由於資產的權重相對較低，$w_{a}^{2}\approx 0$

即新增風險 = $[2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]\quad$

• 市場組合的預期收益 = $(w_{m}\operatorname {E} (R_{m})+[w_{a}\operatorname {E} (R_{a})])$

因此，額外的預期收益 = $[w_{a}\operatorname {E} (R_{a})]$

(2) 如果一項資產 a 的價格被正確定價，那麼將其新增到市場組合 m 中所帶來的風險收益比改善將至少與將這些資金投入市場組合中所帶來的收益相匹配。假設投資者將以無風險利率 $R_{f}$ 借款購買該資產；如果 $\operatorname {E} (R_{a})>R_{f}$，這是合理的。

因此：$[w_{a}(\operatorname {E} (R_{a})-R_{f})]/[2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]=[w_{a}(\operatorname {E} (R_{m})-R_{f})]/[2w_{m}w_{a}\sigma _{m}\sigma _{m}]$

也就是說：$[\operatorname {E} (R_{a})]=R_{f}+[\operatorname {E} (R_{m})-R_{f}]*[\rho _{am}\sigma _{a}\sigma _{m}]/[\sigma _{m}\sigma _{m}]$

也就是說：$[\operatorname {E} (R_{a})]=R_{f}+[\operatorname {E} (R_{m})-R_{f}]*[\sigma _{am}]/[\sigma _{mm}]$

$[\sigma _{am}]/[\sigma _{mm}]\quad$ 是“貝塔係數”，$\beta$ 回報—— 資產回報與市場回報之間的協方差除以市場回報的方差—— 即資產價格對市場組合價值變動的敏感度。

批評

儘管在理論上具有重要意義，但現代投資組合理論的批評者質疑它是否是一種理想的投資策略，因為其金融市場模型在許多方面與現實世界不符。

將理論基礎轉化為可行的投資組合構建演算法的努力一直受到技術困難的困擾，這些困難源於原始最佳化問題相對於可用資料的穩定性。最近的研究表明，當在最佳化過程中加入正則化約束或懲罰項時，此類不穩定性會消失。

假設

現代投資組合理論的框架對投資者和市場做出了許多假設。一些假設在方程中明確表達，例如使用正態分佈對回報進行建模。另一些假設是隱含的，例如忽略稅收和交易費用。這些假設沒有一個是完全正確的，每一個都在一定程度上損害了現代投資組合理論。

• 投資者對上述最佳化問題感興趣（在給定方差的情況下最大化均值）。在現實中，投資者擁有效用函式，這些函式可能對收益分佈的高階矩敏感。為了讓投資者使用均值-方差最佳化，必須假設效用和收益的組合使效用最佳化問題類似於均值-方差最佳化問題。沒有關於收益假設的二次效用就足夠了。另一個假設是使用指數效用和正態分佈，如下所述。

• 資產回報是（聯合）正態分佈隨機變數。事實上，人們經常觀察到，股票和其他市場的回報並非正態分佈。市場中出現的大幅波動（偏離均值的 3 到 6 個標準差）遠遠超過正態分佈假設所預測的。雖然該模型也可以透過假設任何聯合橢圓的收益分佈來證明，但所有聯合橢圓分佈都是對稱的，而資產收益在經驗上並非對稱的。

• 資產之間的相關性是固定的，永遠不變。相關性取決於基礎資產之間的系統性關係，當這些關係發生變化時，相關性也會發生變化。例如，一個國家對另一個國家宣戰，或者發生普遍的市場崩潰。在金融危機期間，所有資產往往都會變得正相關，因為它們都會（向下）一起移動。換句話說，現代投資組合理論恰好在投資者最需要保護免受風險時失效。

• 所有投資者都致力於最大化經濟效用（換句話說，儘可能多地賺錢，而不考慮任何其他因素）。這是現代投資組合理論所依賴的有效市場假說的一個關鍵假設。

• 所有投資者都是理性的，並且厭惡風險。這是有效市場假說的另一個假設，但我們現在從行為經濟學中瞭解到，市場參與者並非理性。它不允許“羊群行為”或願意為更高風險接受更低迴報的投資者。賭場賭徒顯然會為風險付費，一些股票交易者也可能為風險付費。

• 所有投資者都可以在同一時間獲得相同的資訊。事實上，現實市場存在資訊不對稱、內幕交易以及那些比其他人更瞭解資訊的人。此外，估計回報的均值（例如，當在 0 和 T 之間進行子取樣時，布朗運動的漂移沒有一致的估計量）和協方差矩陣（當資產數量與時期數量同階時）是困難的統計任務。

• 投資者對可能的回報有準確的概念，即投資者的機率信念與回報的真實分佈相匹配。另一種可能性是，投資者的預期是有偏見的，導致市場價格缺乏資訊效率。這種可能性在行為金融領域中得到了研究，該領域使用心理假設為資本資產定價模型提供替代方案，例如肯特·丹尼爾、大衛·希爾希利弗和阿瓦尼達爾·蘇布拉曼尼安 (2001) 的基於過度自信的資產定價模型。

• 不存在稅收或交易成本。真實的金融產品會受到稅收和交易成本（例如經紀費用）的影響，考慮這些因素將改變最佳投資組合的構成。這些假設可以透過更復雜的模型來放寬。

• 所有投資者都是價格接受者，即他們的行為不會影響價格。在現實中，單個資產的足夠大的出售或購買可能會改變該資產和其他資產（透過需求的交叉彈性）的市場價格。如果市場在他們購買所需證券時移動過快，投資者甚至可能無法組建理論上的最佳投資組合。

• 任何投資者都可以以無風險利率無限期地借入和貸出。在現實中，每個投資者都有信用額度。

• 所有證券都可以分成任意大小的部分。在現實中，通常不能購買或出售零股，並且某些資產有最低訂單規模。

• 資產的風險/波動率是預先知道的/是恆定的。事實上，市場經常錯誤地定價風險（例如美國抵押貸款泡沫或歐洲債務危機），而波動率正在迅速變化。

更復雜的現代投資組合理論版本可以考慮更復雜的模型（例如具有非正態分佈和稅收的模型），但所有金融數學模型仍然依賴於許多不切實際的前提。

現代投資組合理論實際上並沒有對市場進行建模

現代投資組合理論使用的風險、回報和相關性指標是基於期望值，這意味著它們是關於未來的數學陳述（回報的期望值在上述方程中是明確的，在方差和協方差的定義中是隱含的）。在實踐中，投資者必須用基於資產回報和波動率歷史測量的預測來替代這些方程中的值。這些期望值通常無法考慮到生成歷史資料時不存在的新情況。

更重要的是，投資者被迫從過去的市場資料中估計關鍵引數，因為現代投資組合理論試圖根據損失的可能性對風險進行建模，但沒有說明這些損失可能發生的原因。使用的風險測量本質上是機率性的，而不是結構性的。這與許多工程風險管理方法相比是一個重大差異。

期權理論和現代投資組合理論至少與核電站進行的機率風險評估有一個重要的概念差異。PRA 是經濟學家所說的結構模型。系統及其元件之間的關係在蒙特卡洛模擬中進行建模。如果閥門 X 發生故障，會導致泵 Y 的背壓損失，導致流向容器 Z 的流量下降，等等。

但在布萊克-斯科爾斯方程和現代投資組合理論中，沒有嘗試解釋價格變化的潛在結構。各種結果只是被賦予了機率。而且，與 PRA 不同，如果沒有特定系統級事件（如流動性危機）的歷史記錄，就沒有辦法計算其發生的可能性。如果核工程師以這種方式進行風險管理，他們將永遠無法計算特定工廠發生熔燬的可能性，除非在相同的反應堆設計中發生過幾次類似的事件。

——道格拉斯·W·哈伯德，《風險管理的失敗》，第 67 頁，約翰·威利父子公司，2009 年。 ISBN 978-0-470-38795-5

本質上，現代投資組合理論的數學將市場視為一堆骰子。透過檢查過去的市場資料，我們可以對骰子如何加權形成假設，但這對實際市場依賴於更大、更復雜、更混亂的系統（即世界）的情況沒有幫助。因此，真實的金融市場的精確結構模型不太可能出現，因為它們本質上將是整個世界的結構模型。儘管如此，人們越來越認識到金融市場中系統性風險的概念，這應該會導致更復雜的市場模型。

數學風險測量也只有在它們反映了投資者真實擔憂的程度上才有用——在實踐中，對沒有人關心的變數進行最小化毫無意義。現代投資組合理論使用方差的數學概念來量化風險，這在橢圓分佈收益（例如正態分佈收益）的假設下可能是合理的，但對於一般的收益分佈，其他風險測量（如一致性風險測量）可能更好地反映投資者的真實偏好。

特別是，方差是一種對稱度量，它將異常高的回報視為與異常低的回報一樣危險。有些人會認為，在現實中，投資者只關心損失，並不關心高於平均回報的分散或緊密程度。根據這種觀點，我們對風險的直觀概念本質上是不對稱的。

現代投資組合理論沒有考慮投資決策的個人、環境、戰略或社會維度。它只試圖最大化風險調整後的回報，而不考慮其他後果。從狹義上講，它完全依賴於資產價格，使其容易受到各種標準市場失靈的影響，例如由資訊不對稱、外部性和公共物品引起的市場失靈。它還獎勵企業欺詐和不誠實的會計行為。從更廣泛的意義上講，公司可能具有影響其投資決策的戰略或社會目標，而個人投資者可能具有個人目標。在這兩種情況下，歷史回報以外的資訊都是相關的。

金融經濟學家納西姆·尼古拉斯·塔勒布也批評了現代投資組合理論，因為它假設了高斯分佈

在股市崩盤（1987 年）之後，他們獎勵了兩個人物，哈里·馬科維茨和威廉·夏普，他們基於高斯基礎構建了美麗的柏拉圖模型，並促成了所謂的現代投資組合理論。簡單地說，如果你去除他們的高斯假設，並將價格視為可擴充套件的，那麼你剩下的只是熱空氣。諾貝爾委員會本可以測試夏普和馬科維茨模型——它們的作用就像網際網路上出售的騙人療法——但斯德哥爾摩似乎沒有人考慮過這一點。

現代投資組合理論沒有考慮其對資產價格的影響

多元化投資消除了非系統性風險，但代價是增加了系統性風險。多元化投資迫使投資組合經理在不分析基本面情況下投資資產，僅僅是為了消除投資組合的非系統性風險（CAPM假設投資所有可獲得的資產）。這種人為增加的需求推高了資產價格，而這些資產在單獨分析時，本身基本價值很低。其結果是，整個投資組合變得更加昂貴，因此，正回報的機率下降（即投資組合的風險增加）。

這方面的經驗證據是，股票在被納入標準普爾500等主要指數後通常會經歷價格上漲。

擴充套件

自從MPT在1952年被提出後，人們做了很多嘗試來改進該模型，特別是在採用更現實的假設方面。

後現代投資組合理論透過採用非正態分佈的、不對稱的風險度量來擴充套件MPT。這有助於解決其中一些問題，但不能解決其他問題。

Black-Litterman模型最佳化是對無約束Markowitz最佳化的擴充套件，它結合了對風險和回報的輸入的相對和絕對“觀點”。

其他應用

應用於專案組合和其他“非金融”資產

一些專家將MPT應用於除金融工具以外的專案組合和其他資產。當MPT應用於傳統的金融投資組合之外時，必須考慮不同型別投資組合之間的一些差異。

1. 金融投資組合中的資產在實際應用中是連續可分的，而專案組合是“塊狀的”。例如，雖然我們可以計算出3支股票的最佳投資組合頭寸分別是44%、35%、21%，但專案投資組合的最佳頭寸可能不允許我們簡單地改變在專案上的支出。專案可能是全有全無的，或者至少有不能分割的邏輯單位。投資組合最佳化方法必須考慮到專案的離散性。
2. 金融投資組合的資產是流動性的；它們可以隨時評估或重新評估。但啟動新專案的機會可能是有限的，並且可能出現在有限的時間視窗內。已經啟動的專案不能在沒有損失沉沒成本的情況下放棄（即，半完成的專案幾乎沒有或根本沒有回收/殘值）。

這些情況並不能完全排除使用MPT和此類投資組合的可能性。它們僅僅表明需要使用一組額外的數學表達約束條件來執行最佳化，而這些約束條件通常不適用於金融投資組合。

此外，現代投資組合理論中一些最簡單的要素適用於幾乎任何型別的投資組合。透過記錄投資者在特定回報下可接受的風險程度來捕捉投資者風險偏好的概念，可以應用於各種決策分析問題。MPT使用歷史方差作為風險度量，但像重大專案這樣的資產投資組合沒有明確的“歷史方差”。在這種情況下，MPT投資邊界可以用更通用的術語表達，例如“回報率低於資本成本的可能性”或“損失超過投資金額一半的可能性”。當將風險表述為對預測和可能損失的不確定性時，該概念就可以轉移到各種型別的投資中。

應用於其他學科

在20世紀70年代，現代投資組合理論中的概念被引入區域科學領域。在一系列開創性的著作中，邁克爾·康羅伊使用投資組合理論方法對經濟中的勞動力進行了建模，以考察勞動力的增長和波動性。之後，出現了大量關於經濟增長與波動性之間關係的文獻。

最近，現代投資組合理論被用來對社會心理學中的自我概念進行建模。當構成自我概念的自我屬性構成一個多元化的投資組合時，個體層面的心理結果，如情緒和自尊，應該比自我概念不多元化時更穩定。這一預測已在涉及人類受試者的研究中得到證實。

近年來，現代投資組合理論被應用於資訊檢索中對文件之間不確定性和相關性的建模。給定一個查詢，目標是最大化排名列表中文件的整體相關性，同時最小化排名列表的整體不確定性。

與套利定價理論比較

SML和CAPM通常與套利定價理論（APT）形成對比，後者認為，金融資產的預期回報可以建模為各種宏觀經濟因素的線性函式，其中對每個因素變化的敏感性由特定因素的貝塔係數表示。

APT在其假設方面不太嚴格：它允許資產回報的統計模型，並假設每個投資者將持有具有自己獨特貝塔陣列的獨特投資組合，而不是相同的“市場投資組合”。然而，與CAPM不同的是，APT本身並沒有揭示其定價因素的身份——這些因素的數量和性質可能會隨著時間和經濟體的變化而變化。

進一步閱讀

• Lintner，John (1965)。“風險資產的估值以及股票投資組合和資本預算中風險投資的選擇”。《經濟學與統計學評論》。麻省理工學院出版社。47 (1): 13–39。 doi:10.2307/1924119。 JSTOR 1924119. {{cite journal}}: 引用具有空的未知引數：|month= 和 |coauthors= (幫助)
• Sharpe，William F. (1964)。“資本資產價格：風險條件下市場均衡理論”。《金融雜誌》。19 (3): 425–442。 doi:10.2307/2977928。 JSTOR 2977928. {{cite journal}}: 引用具有空的未知引數：|month= 和 |coauthors= (幫助)
• Tobin, James (1958). "流動性偏好作為對風險的態度". 經濟研究評論. 25 (2): 65–86. doi:10.2307/2296205. JSTOR 2296205. {{cite journal}}: 引用包含空白未知引數：|coauthors= 和 |month= (幫助)

外部連結

• 免費股票投資組合最佳化線上 允許使用者比較股票表現，進行免費股票分析，以及最佳化股票投資組合。
• 宏觀投資分析, 威廉·F·夏普教授，斯坦福大學
• 投資理論導論

, 威廉·N·戈茨曼教授，耶魯管理學院