謎題/哥尼斯堡七橋
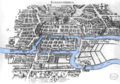
在18世紀早期,有一座名為哥尼斯堡(現稱為加里寧格勒)的城市,它曾是普魯士的一個古老城市(以前是德國的一個飛地,現在屬於俄羅斯),位於普雷戈利亞河畔。這座城市的佈局本身就很獨特,因為克奈普霍夫島(現在稱為康德島)被包圍,有兩個中心陸地由7座橋連線(參見圖1),在古代,如圖所示。
據說,這七座橋分別稱為鐵匠橋、連線橋、綠橋、商人橋、木橋、高橋和蜂蜜橋。
哥尼斯堡的市民過去常常在星期天下午在他們美麗的城市裡散步。在散步的時候,市民們決定為自己創造一個遊戲,他們的目標是設計一種方法,讓他們可以繞著城市散步,只穿過這七座橋一次,並且只走一次。儘管哥尼斯堡的市民中沒有人能設計出一條路線讓他們只穿過每座橋一次,但他們仍然無法證明這是不可能的。
不幸的是,在哥尼斯堡,事情並沒有那麼順利。普魯士解體後,哥尼斯堡最終成為俄羅斯的一部分(自那以後,這座城市被改名為加里寧格勒)。二戰期間,盟軍在1942年炸燬了兩座原始的橋,並在戰後重建。後來又拆除了另外兩座橋,為高速公路讓路。現在,在21世紀,人們可以利用剩下的五座橋,在一次散步中完成繞城市的旅程。
萊昂哈德·尤拉(參見圖2),一位瑞士數學家,對這個問題很感興趣,當時,幾何、代數甚至計數的藝術都不足以解決它。
1735年8月,尤拉發表了一篇題為“Solutio problematis ad geometriam situs pertinentis”的論文。
在這篇論文的第一段中,尤拉指出,他認為這個問題與幾何有關,但並非他同時代人所熟知的測量和計算的幾何,而是他稱之為位置幾何的一種新型幾何。
他指出,每個陸地內部的路線選擇並不重要。路線的唯一重要屬性是穿越橋樑的順序。因此,他將問題抽象化了。尤拉提供了這個問題的草圖,並刪除了地圖的所有特徵,除了陸地的清單(他用A、B、C、D標記)和連線它們的橋樑(a、b、c、d、e、f、g)。(參見圖3)他提出了這個問題的一般問題,“能否確定是否可以正好穿過每座橋一次?”
在第三段中,尤拉告訴讀者,為了解決這個問題,他可以寫下所有可能的路徑,但這種方法將花費大量時間,而且對於具有更多橋樑和陸地的更大的配置,這種方法將不起作用。由於這些問題,尤拉決定選擇另一種方法來解決這個問題。
在第四段和第五段中,尤拉開始簡化問題,用抽象的“頂點”或節點代替每個陸地。然後,他用抽象的連線,即“邊”來代替每座橋。邊(道路)記錄了哪些頂點(陸地)是連線的。這樣,他就形成了一個圖。每個交叉點將被標記如下:如果交叉點從陸地A到陸地B,它將被稱為AB。(參見圖4)
在第五段中,尤拉繼續討論這個過程,解釋說在ABDC中,儘管有四個大寫字母,但只穿過了三座橋。尤拉解釋說,無論有多少橋,都會多一個字母來表示必要的穿越。因此,哥尼斯堡七橋問題需要穿越七座橋,因此實際上,需要八座橋才能穿越。
總而言之,尤拉指出,“一般來說,如果橋樑的數量是任何奇數,並且增加1,那麼A出現的次數就是結果的一半。”這意味著,每座橋都有兩個端點,每個橋的端點都位於其他陸地。因此,橋樑端點的數量等於橋樑數量的兩倍,並且始終是一個偶數。當我們在一個區域中計算橋樑連線的數量時,我們是在計算橋樑的端點。因此,如果某個區域有奇數個連線,那麼肯定還有另一個區域有奇數個連線,因為所有橋樑端點的總和必須是偶數。
-
圖1:帶有河流和橋樑的舊哥尼斯堡地圖,顏色標註
-
圖2:萊昂哈德·尤拉的肖像
-
圖3:萊昂哈德·尤拉關於哥尼斯堡橋的草圖
-
圖4:哥尼斯堡七橋的簡化