半導體/摻雜

半導體

在檢查晶體時，我們為了簡便起見，對它們做了一些假設，例如

雖然無限的說法有點模糊，但這是一個相當好的近似，因為這些晶體通常比晶體內部的距離大得多。

由於晶體存在於3D空間中並且是週期性的，如果我們在其中一個軸上移動晶體的大小，我們將處於一個對應的位置。在數學上，我們說我們有三個線性無關的向量，並且可以移動它們的整數值到晶格中的對應位置。

$\mathbf {r} =u\mathbf {a} +v\mathbf {b} +w\mathbf {c}$

晶胞

如果我們有一個晶格，它一定是由更小的元件組成的，晶胞是晶格中最小的不可分割的部分。透過將許多晶胞放在一起，您可以再次建立整個晶格。想象一堆骰子，你可以說一個骰子是這個晶體晶格的晶胞。

存在無限數量的可能的晶胞，但只有 14 種類型的晶格。這可以推廣到 7 個晶體類。

此外，晶胞存在最小尺寸，其體積為 1 個晶格點（原子/分子/任何東西）。

想象一個立方晶胞，每個角都有一個點。所以總共有 8 個點，但這些點中的每一個都與它和其他 7 個立方體共享。

所以每個晶胞的晶格點數為 8 * 1/8 = 1。我們稱之為原胞。

現在，如果我們將每個點想象成一個與相鄰點接觸的球體，那麼我們可以將填充率定義為點所佔體積與晶胞體積的比率。

在立方晶胞中，每個球體的半徑將是晶體大小的一半。所以我們說 r = a/2。

V_{point}={\frac {4}{3}}\pi r^{3}={\frac {4}{3}}\pi \left({\frac {a}{2}}\right)^{3}

並且每個晶胞中只有一個，即原胞 = 1。所以

PackingFraction={\frac {V_{point}}{V_{cell}}}={\frac {{\frac {4}{3}}\pi \left({\frac {a}{2}}\right)^{3}}{a^{3}}}={\frac {\pi }{6}}

或 52%

就像一個立方晶胞，除了在它的中心還有一個晶格點。

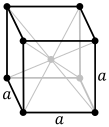
原胞 = 8 * 1/8 + 1 = 2。

它的填充率為 68%。

這是一個密堆積晶格，它就像一個立方體，只是所有 6 個面都在它們的中心有另一個點。

原胞 = 8 * 1/8 + 6 * 1/2 = 4

填充率 = 74%