訊號與系統/頻率響應

頻率響應

系統對不同頻率的輸入訊號有不同的響應。某些系統可能放大某些頻率的成分，而衰減其他頻率的成分。系統輸出與系統輸入在不同頻率上的關係被稱為系統的頻率響應。

頻率響應是系統輸入和輸出在傅立葉域的關係。

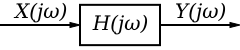
在這個系統中，X(jω) 是系統輸入，Y(jω) 是系統輸出，H(jω) 是頻率響應。我們可以定義這些函式之間的關係為

$Y(j\omega )=H(j\omega )X(j\omega )$

${\frac {Y(j\omega )}{X(j\omega )}}=H(j\omega )$

頻率響應函式

由於頻率響應是一個複數函式，我們可以將其轉換為複平面上的極座標形式。這將給我們一個幅值和一個角度。我們將這個角度稱為相位。

幅頻響應

對於每個頻率，幅值表示系統放大或衰減輸入訊號的趨勢。

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|$

相頻響應

相位表示系統改變輸入正弦訊號相位的趨勢。

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)$.

相頻響應，或其導數群延遲，告訴我們系統如何延遲輸入訊號作為頻率的函式。

例子

例子：電路

考慮以下具有相量輸入和輸出電壓的通用電路

其中

$V_{o}\left({j\omega }\right)=V_{om}\cos \left({\omega t+\theta _{o}}\right)=V_{om}\angle \theta _{o}$

$V_{i}\left({j\omega }\right)=V_{im}\cos \left({\omega t+\theta _{i}}\right)=V_{im}\angle \theta _{i}$

和之前一樣，我們可以將這個電路的系統函式H(jω)定義為

$H\left({j\omega }\right)={{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}$

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|={{\left|{V_{o}\left({j\omega }\right)}\right|} \over {\left|{V_{i}\left({j\omega }\right)}\right|}}={{V_{om}} \over {V_{im}}}$

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)=\angle \left({{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}\right)=\angle V_{o}\left({j\omega }\right)-\angle V_{i}\left({j\omega }\right)=\theta _{o}-\theta _{i}$

重新排列得到以下轉換

$V_{om}=A\left(\omega \right)V_{im}$

$\theta _{o}=\theta _{i}+\phi \left(\omega \right)$

示例：低通濾波器

我們將使用一個簡單的低通濾波器作為示例來說明這種方法。這種型別的電路允許低頻透過，但阻止高頻。

求解以下 RC 電路的頻率響應函式，進而求解幅度和相位響應函式（已處於相量形式）。

首先，我們使用分壓器規則根據輸入相量得到輸出相量。

$V_{o}\left({j\omega }\right)=V_{i}\left({j\omega }\right)\cdot {{1 \over {j\omega C}} \over {R+{1 \over {j\omega C}}}}$

現在我們可以很容易地確定頻率響應。

$H\left({j\omega }\right)={{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}={{1 \over {j\omega C}} \over {R+{1 \over {j\omega C}}}}$

簡化後得到：

$H\left({j\omega }\right)={1 \over {1+j\omega RC}}$

由此我們可以得到幅度和相位響應

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|={1 \over {\sqrt {1+\left({\omega CR}\right)^{2}}}}$

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)=\tan ^{-1}\left({0 \over 1}\right)-\tan ^{-1}\left({{\omega RC} \over 1}\right)=-\tan ^{-1}\left({\omega RC}\right)$

頻率響應由幅度和相位響應的圖形表示

當這些圖形在適當的對數刻度上繪製時，通常更容易解釋

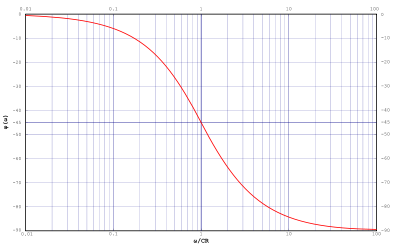
這表明該電路確實是一個濾除較高頻率的濾波器。這種濾波器被稱為低通濾波器。

可以使用稱為頻譜分析儀或增益和相位測試儀的儀器繪製任意電路的幅度和相位響應。有關使用這些儀器的更多詳細資訊，請參見實用電子學。

濾波器

從這些示例中可以得出的一個重要概念是，透過設計一個稱為濾波器的適當系統，我們可以選擇性地衰減或放大某些頻率範圍。這意味著我們可以最小化某些不希望的頻率成分（例如噪聲或競爭資料訊號），並最大化我們自己的資料訊號

我們可以將“接收訊號”r定義為資料訊號d和不希望的成分v的組合

$r(t)=d(t)+v(t)$

我們可以取r的能量譜密度來確定資料訊號d的頻率範圍。我們可以設計一個試圖放大這些頻率範圍並衰減v的頻率範圍的濾波器。我們將在接下來的幾章中討論這個問題和濾波器的一般問題。有關此主題的更深入討論，請參閱訊號處理書籍。