時域中的聲音

聲波的出現和行為

聲音的度量（聲學）定義是壓力波和密度的變化，這是由波在介質中的傳播引起的。在約 25Hz 到 18kHz 之間，人類的聽覺系統會感知到這些波，因為它們會導致耳鼓運動。這種機械運動在耳蝸中被轉化為神經衝動，並被髮送到大腦的聽覺區域進行分析。聲波是隨著時間的推移而變化的氣壓，可以用隨著時間的推移而變化的電壓或資料流來表示。這是一種聲音的“時間/幅度”表示，也稱為幅度時間線。幅度表示氣壓變化引起的分子位移。在數字域中，幅度通常表示為1到-1之間的值，其中1和-1表示訊號的最大正值和負值幅度，而0表示零幅度。

圖 1.1中的波形稱為正弦波或正弦。正弦波可以被認為是聲音的基本組成部分。該圖表明幅度隨時間變化，但這種變化模式週期性地重複。

圖 1.2中的波形比1.1中的正弦波更復雜。存在不同幅度的峰值和谷值，並且儘管模式隨著時間的推移而重複（看看你是否能找到它），但它更難發現。正如正弦波以簡單的方式表現並聽起來簡單一樣，這種聲音以更大的複雜性表現並也聽起來更復雜。因此，隨時間變化的詳細、複雜的聲音在如此近距離檢視時往往沒有可辨別的特徵——可能沒有重複的模式或行為，我們可以用它來告訴我們關於聲音的資訊。

在圖 1.3中，我們看到了一種聲音在約 2 秒而不是 2 毫秒內的外觀。從這個角度來看，我們可以看到整體聲音幅度隨時間的變化方式；特別地，高幅度部分可以很容易地被視為鼓聲——它們突然出現並且迅速降低幅度，正如人們對敲擊鼓面所期望的那樣。如果這種聲音是在幾毫秒的範圍內觀察到的，那麼可能很難判斷是哪種樂器在演奏。由此，我們應該得出結論，短時間間隔和長時間間隔的視角都顯示了不同型別的資訊，並且選擇適合自己需求的正確視角非常重要。

正弦波、頻率和音高

如圖 1.1所示，正弦波具有周期性形式，每 $T\,$ 秒重複一次，稱為週期，迴圈。該波還具有正最大幅度， $A\,$ ，以及負最大幅度， $-A\,$ 。正弦波的頻率， $f\,$ ，是每秒的迴圈次數，以赫茲（Hz）為單位測量。我們可以從以下公式中獲得頻率從波長

f={\frac {1}{T}}\,

此外，我們可以用以下數學形式來表示正弦波（角度以弧度表示）。這種形式可能對有興趣在程式碼中建立自己的可控正弦函式的程式設計師有用

p(t)=Asin\left({\frac {2\pi t}{T}}\right)=Asin(2\pi ft)

從心理測量學來看，較高的頻率（例如高於 1.5kHz）通常與“明亮”等詞語相關聯，而較低的頻率（例如低於 200Hz）通常與“深度”或“低音”等詞語相關聯。中間範圍可能與“溫暖”一詞相關聯。例如，一種樂器，如以乾淨的方式演奏的電吉他，可能會被稱為“明亮”或“尖銳”，而一把低音提琴可能會被稱為“暗淡”和“溫暖”。由於是心理測量學，這些術語不是我們可以精確測量的客觀量，而是經常用來描述特定聲音的音色或音調顏色。聲音中存在的不同頻率的各種幅度，以及它們隨著時間的推移而演變是與音色相關的主要因素，並且可以透過組成聲音的不同頻率的組合來實現無限的音色。在心理測量學方面，人類聽覺將整數頻率比與音高相關聯，並將特定頻率與標準西方音階中的特定音符相關聯

波長 (t)	頻率 (Hz)	音符名稱
156.82 釐米	220.0	A3
139.71 釐米	246.94	B3
131.87 釐米	261.63	C4
117.48 釐米	293.66	D4
104.66 釐米	329.63	E4
98.79 釐米	349.23	F4
88.01 釐米	392.0	G4
78.41 釐米	440.0	A4

圖 1.4。波長、頻率和音符名稱之間的關係。

請注意，此表涵蓋了八度的範圍。頻率加倍，波長減半。

正弦波的構造和解構

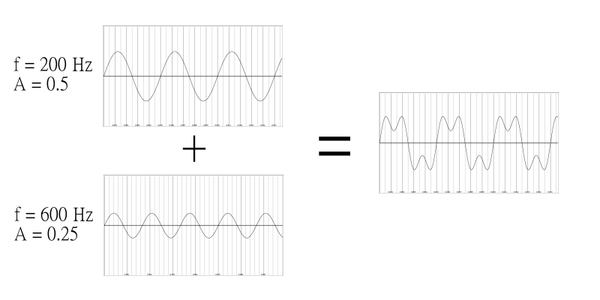
利用傅立葉分析，正弦波可以被認為是聲音的基本組成部分，因為單個正弦波是單個頻率。在傅立葉分析中，結合不同頻率、幅度和相位的正弦波可以重建任何聲音的頻譜。類似地，複雜的聲音可以根據頻率、幅度和相位進行分析。

圖 1.5展示了兩個正弦波加在一起的外觀。兩個波的特性在結果波形中結合在一起。這種技術是加法合成的基礎，這將在本書的後面部分討論。此外，在聲音的構建方式中，可以從整體中濾除兩個組成頻率；這通常透過在頻域中分析波形來完成，這將在下一章中討論。