狹義相對論/動力學

介紹

由於相對論理論，粒子速度在相對運動的觀察者之間存在差異的方式意味著動量需要重新定義。

下圖顯示了兩個粒子的典型碰撞。在右手系中，碰撞是從與其中一個粒子以相同速度運動的觀察者的角度觀察的，在左手系中，它是從以介於兩個粒子速度之間的速度運動的觀察者的角度觀察的。

如果重新定義動量，那麼所有變數（如力（動量變化率）、能量等）都將被重新定義，相對論將導致完全新的物理學。新物理學透過關係 $K=\gamma mc^{2}-mc^{2}\,$ 對普通體驗產生影響，因此它是伽馬與1之間的微小偏差，以日常動能的形式表達出來，因此整個物理學都與“相對論”推理有關，而不是牛頓的經驗觀點。

動量

在物理學中，動量在一個封閉的系統中是守恆的，動量守恆定律適用。考慮以下所示的相同粒子對稱碰撞的特例

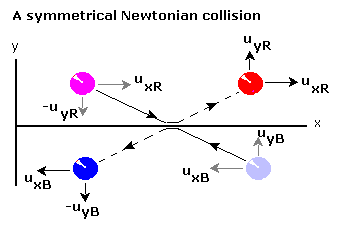
紅色球的動量變化是

$2m\mathbf {u_{yR}}$

藍色球的動量變化是

$-2m\mathbf {u_{yB}}$

情況是對稱的，因此證明了牛頓動量守恆定律

$2m\mathbf {u_{yR}} =2m\mathbf {u_{yB}}$

請注意，此結果取決於速度的 y 分量相等，即 $\mathbf {u_{yR}} =\mathbf {u_{yB}}$.

相對論情況則大不相同。碰撞如下圖所示，左手系顯示了碰撞在一位觀察者看來是什麼樣子，而右手系顯示了完全相同的碰撞在與藍色球以相同速度運動的另一位觀察者看來是什麼樣子

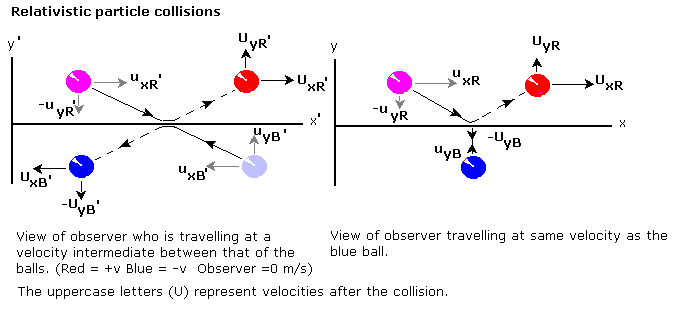
上面所示的配置已簡化，因為一個系包含一個靜止的藍色球（即：$u_{xB}=0$）並且速度的選擇使得紅色球的垂直速度在碰撞後正好反轉，即：$u_{yR}^{'}=u_{yB}^{'}$。這兩個系都顯示了完全相同的事件，只有觀察者在不同的系之間有所不同。系之間的相對論速度變換是

$u_{yR}^{'}={\frac {u_{yR}{\sqrt {1-v^{2}/c^{2}}}}{1-u_{xR}v/c^{2}}}$

$u_{yB}^{'}={\frac {u_{yB}{\sqrt {1-v^{2}/c^{2}}}}{1-u_{xB}v/c^{2}}}=u_{yB}{\sqrt {1-v^{2}/c^{2}}}$ 給定$u_{xB}=0\,$.

假設在某個參考系中 y 分量相等，在牛頓物理學中，它們在另一個參考系中也將相等。然而，在相對論中，如果在某個參考系中 y 分量相等，它們在另一個參考系中不一定相等（時間膨脹不是方向性的，因此垂直速度在觀察者之間不同）。例如，如果$u_{yR}^{'}=u_{yB}^{'}$，則

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

因此，如果$u_{yR}^{'}=u_{yB}^{'}$，那麼在這種情況下$u_{yR}\neq u_{yB}$.

如果在碰撞之間和參考系之間質量是恆定的，那麼儘管$2mu_{yR}^{'}=2mu_{yB}^{'}$，人們發現

$2mu_{yR}\neq 2mu_{yB}$

因此，定義為質量乘以速度的動量在碰撞中不守恆，當碰撞在彼此相對運動的參考系中描述時。請注意，如果$u_{xR}$和$v$很小，這種差異非常小。

為了在所有慣性參考系中保持動量守恆原理，動量的定義必須改變。新的定義必須在物體以遠小於光速的速度運動時簡化為牛頓表示式，以便恢復牛頓公式。

當觀察者以與藍色球體相同的速度運動時，即當$u_{xB}=0\,$時，y 方向上的速度由以下方程關聯：

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

如果我們將藍球的質量記為 $m_{B}$，紅球的質量記為 $m_{R}$（從藍球的參考系觀察），那麼如果相對論原理成立

$2m_{R}u_{yR}=2m_{B}u_{yB}\,$

所以

$m_{R}=m_{B}{\frac {u_{yB}}{u_{yR}}}$

但是

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

因此

$m_{R}={\frac {m_{B}}{1-u_{xR}v/c^{2}}}$

這意味著，如果相對論原理要成立，那麼為了使動量守恆定律成立，質量必須按上述方程所示的量變化。

粒子速度的選擇使得 $u_{yR}^{'}=u_{yB}^{'}$。 $v$ 的選擇使得 $v=u_{xR}^{'}$。 這允許 $v$ 用 $u_{xR}\,$ 表示

$u_{xR}^{'}={\frac {u_{xR}-v}{1-u_{xR}v/c^{2}}}=v$

因此

$v={\frac {c^{2}}{u_{xR}}}(1-{\sqrt {1-u_{xR}^{2}/c^{2}}})$

所以將 $v$ 代入 $m_{R}={\frac {m_{B}}{1-u_{xR}v/c^{2}}}$

$m_{R}={\frac {m_{B}}{\sqrt {1-u_{xR}^{2}/c^{2}}}}$

藍色球體處於靜止狀態，因此它的質量有時被稱為它的靜止質量，並用符號 $m$ 表示。由於球體在加速開始時是相同的，紅色球體的質量是一個藍色球體相對於觀察者運動時的質量；這個質量有時被稱為相對論質量，用符號 $M$ 表示。這些術語現在很少在現代物理學中使用，將在本節末尾解釋。上述討論與藍色球體和紅色球體的相對運動有關，因此 $u_{xR}$ 對應於相對於藍色球體靜止的觀察者而言的運動球體的速度。這些考慮意味著相對論質量由下式給出：

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

相對論動量由相對論質量和速度的乘積給出 $\mathbf {p} =M\mathbf {u}$.

動量相對於靜止質量的整體表達式為：

$\mathbf {p} ={\frac {m\mathbf {u} }{\sqrt {1-u^{2}/c^{2}}}}$

動量的分量為：

$p_{x}={\frac {mu_{x}}{\sqrt {1-u^{2}/c^{2}}}}$

$p_{y}={\frac {mu_{y}}{\sqrt {1-u^{2}/c^{2}}}}$

$p_{z}={\frac {mu_{z}}{\sqrt {1-u^{2}/c^{2}}}}$

因此，動量的分量取決於相應的速度分量和速度。

由於帶有平方根的因子寫起來很麻煩，所以經常使用以下縮寫，稱為洛倫茲伽馬因子：

$\gamma ={\frac {1}{\sqrt {1-u^{2}/c^{2}}}}$

動量的表示式然後寫成 $\mathbf {p} =m\gamma \mathbf {u}$.

從上面的討論可以看出，我們可以將以速度 $\mathbf {u}$ 運動的物體的動量寫成速度 $u$ 的函式 $M(u)$ 和速度 $\mathbf {u}$ 的乘積：

$M(u)\mathbf {u}$

函式 $M(u)$ 必須在低速下簡化為物體的質量 $m$，特別是在物體靜止時 $M(0)=m$。

關於相對論中“質量”一詞的用法存在爭議。如果慣性質量是根據動量定義的，那麼它確實會隨著 $M=\gamma m$ 變化，對於具有靜止質量的單個粒子來說，此外，正如將在下面展示的那樣，具有靜止質量的粒子的能量由 $E=Mc^{2}$ 給出。在關於命名法的爭論之前，函式 $M(u)$ 或關係 $M=\gamma m$，被稱為“相對論質量”，它在粒子框架中的值被稱為“靜止質量”或“不變質量”。相對論質量，$M=\gamma m$，會隨著速度增加。這兩個術語現在在很大程度上已經過時了：“靜止質量”今天簡稱為質量，“相對論質量”通常不再使用，因為正如將在下面關於能量的討論中看到的那樣，它與能量相同，只是單位不同。

力

牛頓第二定律指出作用在粒子上的合力等於其動量變化率。牛頓第二定律的相同形式在相對論力學中仍然成立。相對論的*3 力* 由下式給出

$\mathbf {f} =d\mathbf {p} /dt$

如果使用相對論質量

${\frac {d\mathbf {p} }{dt}}={\frac {d(m\mathbf {u} )}{dt}}$

根據萊布尼茲定律，其中 $d(xy)=xdy+ydx$

$\mathbf {f} ={\frac {d\mathbf {p} }{dt}}=m{\frac {d\mathbf {u} }{dt}}+\mathbf {u} {\frac {dm}{dt}}$

這個關於力的方程將在下面用來推匯出粒子能量的相對論表示式，這些表示式基於“相對論質量”的舊概念。

相對論力也可以用加速度來表示。牛頓第二定律可以寫成熟悉的形式

$\mathbf {F} =m\mathbf {a}$

其中 $\mathbf {a} =d\mathbf {v} /dt$ 是加速度。

這裡的 m 不是 相對論質量，而是不變質量。

在相對論力學中，動量為 $\mathbf {p} =m\gamma \mathbf {v}$

其中 m 是不變質量，力由 $\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=m{\frac {d(\gamma \mathbf {v} )}{dt}}$

這種力的形式被用於推匯出能量表達式，而無需依賴相對論質量。

在本書的第二部分，我們將看到，牛頓第二定律用加速度表示為

$\mathbf {F} =m\gamma (\mathbf {a} +{\frac {\gamma ^{2}v}{c^{2}}}{\frac {dv}{dt}}\mathbf {v} )$

能量

關於使用“相對論質量”概念的爭論意味著現代物理課程可能禁止在能量推導中使用它。使用相對論質量的較新能量推導在第一部分給出，而使用相對論質量的較舊推導在第二部分給出。這兩種推導可以進行比較，以深入瞭解關於質量的爭論，但真正需要了解 4 向量才能深入討論這個問題。原則上，第一個推導在數學上是最正確的，因為“相對論質量”由下式給出：$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$，其中包含常數 $m$ 和 $c$.

使用相對論動量推導相對論能量

在下文中，現代推導中，m 表示不變質量——過去稱為“靜止質量”。能量被定義為將物體從一個地方移動到另一個地方所做的功。我們將使用相對論動量 $p=\gamma mv$。能量由下式給出

$dE=\mathbf {f} d\mathbf {x}$

因此，在整個路徑上

$E=\int _{0}^{x}\mathbf {f} d\mathbf {x}$

動能 (K) 是將物體從速度 0 移動到速度 $\mathbf {u}$ 所使用的能量。將運動限制在一個維度

$K=\int _{u=0}^{u=u}\mathbf {f} dx$

使用相對論的 *3 力*

$K=\int _{u=0}^{u=u}{\frac {d(m\gamma u)}{dt}}dx=\int _{u=0}^{u=u}m{\frac {d(\gamma u)}{dt}}dx=\int _{u=0}^{u=u}md(\gamma u){\frac {dx}{dt}}$

用 $d(\gamma u)$ 代替，並使用 $dx/dt=u$

$K=\int _{u=0}^{u=u}m(\gamma du+ud\gamma )u$

這將給出

$K=\int _{u=0}^{u=u}m(u\gamma du+u^{2}d\gamma )$

洛倫茲因子 $\gamma$ 由以下給出

$\gamma ={\frac {1}{\sqrt {1-u^{2}/c^{2}}}}$

意味著

$d\gamma ={\frac {u}{c^{2}}}\gamma ^{3}du$

$du={\frac {c^{2}}{u\gamma ^{3}}}d\gamma$

所以

$K=\int _{\gamma =1}^{\gamma =\gamma }m(u\gamma {\frac {c^{2}}{u\gamma ^{3}}}d\gamma +u^{2}d\gamma )=\int _{\gamma =1}^{\gamma =\gamma }m({\frac {c^{2}}{\gamma ^{2}}}+u^{2})d\gamma =\int _{\gamma =1}^{\gamma =\gamma }mc^{2}d\gamma$

或者，我們可以利用以下事實

$\gamma ^{2}c^{2}-\gamma ^{2}u^{2}=c^{2}\,$

求導

$2\gamma c^{2}d\gamma -\gamma ^{2}2udu-u^{2}2\gamma d\gamma =0\,$

所以，重新整理

$\gamma udu+u^{2}d\gamma =c^{2}d\gamma \,$

在這種情況下

$K=\int _{u=0}^{u=u}m(u\gamma du+u^{2}d\gamma )=\int _{u=0}^{u=u}mc^{2}d\gamma \,$

當 $u$ 從 0 到 $u$ 變化時，洛倫茲因子 $\gamma$ 從 1 到 $\gamma$ 變化，所以

$K=mc^{2}\int _{\gamma =1}^{\gamma =\gamma }d\gamma \,$

因此

$K=\gamma mc^{2}-mc^{2}\,$

量 $\gamma mc^{2}$ 稱為粒子的總能量。量 $mc^{2}$ 稱為粒子的靜止能量。如果粒子的總能量用符號 $E$ 表示

$E=\gamma mc^{2}=mc^{2}+K\,$

因此可以看出 $mc^{2}$ 是靜止質量的能量。這種能量被稱為質量能。

牛頓近似動能可以透過使用二項式定理展開 $\gamma =(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$ 推匯出來。

二項式展開為

$(a+x)^{n}=a^{n}+na^{n-1}x+{\frac {n(n-1)}{2!}}a^{n-2}x^{2}....$

因此，展開 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

$K={\frac {1}{2}}mu^{2}+{\frac {3mu^{4}}{8c^{2}}}+{\frac {5mu^{6}}{16c^{4}}}+...$

因此，如果$u$遠小於$c$

$K={\frac {1}{2}}mu^{2}$

這是低速下的牛頓近似值。

利用相對論質量概念推導相對論能量

能量定義為將物體從一個地方移動到另一個地方所做的功。能量來自

$dE=\mathbf {F} d\mathbf {x}$

因此，在整個路徑上

$E=\int _{0}^{x}\mathbf {F} d\mathbf {x}$

動能（K）是將物體從速度為 0 移動到速度為$u$所需的能量。因此

$K=\int _{u=0}^{u=u}Fdx$

使用相對論力

$K=\int _{u=0}^{u=u}{\frac {d(Mu)}{dt}}dx$

所以

$K=\int _{u=0}^{u=u}d(Mu){\frac {dx}{dt}}$

將$d(Mu)$代入並使用$dx/dt=u$

$K=\int _{u=0}^{u=u}(Mdu+udM)u$

這將給出

$K=\int _{u=0}^{u=u}(Mudu+u^{2}dM)$

相對論質量由下式給出

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

可以擴充套件為

$M^{2}c^{2}-M^{2}u^{2}=m^{2}c^{2}$

求導

$2Mc^{2}dM-M^{2}2udu-u^{2}2MdM=0$

所以，重新整理

$Mudu+u^{2}dM=c^{2}dM$

在這種情況下

$K=\int _{u=0}^{u=u}(Mudu+u^{2}dM)$

可以簡化為

$K=\int _{u=0}^{u=u}c^{2}dM$

但質量從 $m$ 變為 $M$，所以

$K=c^{2}\int _{M=m}^{M=M}dM)$

因此

$K=Mc^{2}-mc^{2}$

數量 $Mc^{2}$ 被稱為粒子的總能量。數量 $mc^{2}$ 被稱為粒子的靜止能量。如果粒子的總能量用符號 $E$ 表示

$E=mc^{2}+K$

因此可以看出 $mc^{2}$ 是靜止質量的能量。這種能量被稱為質量能，是著名的公式 $E=mc^{2}$ 的起源，該公式是原子時代的標誌性公式。

可以透過用靜止質量代替相對論質量來推匯出動能的牛頓近似，即

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

以及

$K=Mc^{2}-mc^{2}$

所以

$K={\frac {mc^{2}}{\sqrt {1-u^{2}/c^{2}}}}-mc^{2}$

即

$K=mc^{2}((1-u^{2}/c^{2})^{-{\frac {1}{2}}}-1)$

可以使用二項式定理展開 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

二項式定理是

$(a+x)^{n}=a^{n}+na^{n-1}x+{\frac {n(n-1)}{2!}}a^{n-2}x^{2}....$

因此，展開 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

$K={\frac {1}{2}}mu^{2}+{\frac {3mu^{4}}{8c^{2}}}+{\frac {5mu^{6}}{16c^{4}}}+...$

因此，如果$u$遠小於$c$

$K={\frac {1}{2}}mu^{2}$

這是低速下的牛頓近似。

核能

當質子和中子（核子）結合形成元素時，粒子結合後的狀態往往比自由中子和質子具有更低的能量狀態。鐵具有最低的能量，而鐵在原子質量尺度上上下方的元素往往具有更高的能量。這種隨著中子和質子結合而能量降低的現象被稱為 **結合能**。元素的原子質量略微偏離了其組成粒子計算出的原子質量，這種質量能量差，從 $E=mc^{2}$ 計算，幾乎完全等於結合能。

結合能可以透過將每個核子質量更高的元素轉化為每個核子質量更低的元素來釋放。這可以透過兩種方式實現：一是將鈾等重元素裂變為鋇和氪等輕元素，二是將氫等輕元素聚變為氘等重元素。如果原子被分裂，這個過程被稱為 **核裂變**；如果原子被合併，這個過程被稱為 **核聚變**。比鐵輕的原子可以發生聚變釋放能量，而比鐵重的原子可以發生裂變釋放能量。

當氫和中子結合形成氘時，釋放的能量可以按如下方式計算：

質子的質量為 1.00731 amu，中子的質量為 1.00867 amu，氘核的質量為 2.0136 amu。氘核與其組成粒子之間質量差為 0.00238 amu。這個質量差對應的能量為

$E=mc^{2}=1.66\times 10^{-27}\times 0.00238\times (3\times 10^{8})^{2}$

所以釋放的能量為 $3.57\times 10^{-13}$ 焦耳，大約是 $2\times 10^{11}$ 焦耳每克質子（電離氫）。

(假設 1 amu = $1.66\times 10^{-27}$ 千克，阿伏伽德羅常數 = $6\times 10^{23}$，光速為 $3\times 10^{8}$ 米每秒)

現在的核反應堆使用一種被稱為 **核裂變** 的過程，其中鈾棒釋放中子，這些中子與鈾棒中的鈾結合產生鈾同位素，例如 ²³⁶U，它會迅速衰變為更小的原子核，例如鋇和氪，以及三個中子，這些中子會導致更多 ²³⁶U 的產生和進一步的衰變。每個中子可以引起三個中子的產生，這意味著可以發生 **鏈式反應**。能量的產生源於質量和能量的等價性；衰變產物鋇和氪的質量比原來的 ²³⁶U 低，缺少的質量以 177 MeV 的輻射形式釋放。²³⁶U 衰變的核反應方程式如下：

$_{92}^{236}U\rightarrow _{56}^{144}Ba+_{36}^{89}Kr+3n+177MeV$

核爆炸

如果大量的鈾同位素 ²³⁵U（**臨界質量**）被限制在一個封閉的空間內，鏈式反應就會失控，並幾乎瞬間釋放大量的能量。一種限制臨界質量鈾的裝置被稱為 **原子彈** 或 **A 武器**。一種基於氘原子聚變的炸彈被稱為 **熱核彈**、**氫彈** 或 **H 武器**。