狹義相對論/數學方法

向量

物理效應涉及事物對其他事物的作用，從而產生位置、張力等的改變。這些效應通常取決於相互作用事物的強度、接觸角、分離等，而不是任何絕對參考系，因此用相互作用事物的相對位置和長度來描述支配相互作用的規則是有用的，而不是用任何固定的視點或座標系來描述。向量被引入物理學以允許這種相對描述。

在初級物理學中使用向量往往會迴避對它們的真正理解。它們是一個新的概念，就像數字本身一樣獨特，它們透過一系列公式與其他數學和幾何聯絡起來，例如線性組合、標量積等。

向量被定義為“有向線段”，這意味著它們是在特定方向上繪製的線。將時間作為幾何實體引入意味著這個向量定義有點過時，一個更好的定義可能是，向量是按照空間和時間中連續點序列排列的資訊。向量有長度和方向，方向是從早到晚。

向量用箭頭符號終止的線表示以顯示方向。一個從左向右移動大約三釐米的點可以表示為

如果向量在座標系內表示，它在該系統的每個軸上都有分量。這些分量通常不從座標系的原點開始。

由粗箭頭表示的向量在座標軸上具有分量 a、b 和 c，這些分量是座標軸上的長度。如果向量從原點開始，則分量僅成為向量終點的座標，向量被稱為終點的位矢。

向量的加法

如果兩個向量連線起來，使得一個向量的終點是下一個向量的起點，則這兩個向量的和被定義為從第一個向量的起點到第二個向量的終點繪製的第三個向量

c 是 a 和 b 的和

c = a + b

如果 a 的分量為 x1、y1、z1，而 b 的分量為 x2、y2、z2，則這兩個向量之和的分量為 (x1+x2)、(y1+y2) 和 (z1+z2)。換句話說，當向量相加時，是分量在數值上相加，而不是向量本身的長度。

向量加法的規則

1. 交換律 a + b = b + a

2. 結合律 (a + b) + c = a + (b + c)

如果零向量（沒有長度）標記為 0

3. a + (-a) = 0

4. a + 0 = a

向量乘以標量的規則

對分量和向量加法的討論表明，如果向量 a 具有分量 a、b、c，則 qa 具有分量 qa、qb、qc。向量乘法的意義如下所示

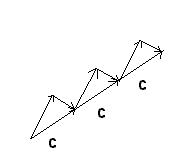
下面的向量 c 被加了三次，這相當於將它乘以 3。

1. 分配律 q(a + b) = qa + qb 和 (q + p)a = qa + pa

2. 結合律 q(pa) = qpa

還有 1 a = a

如果向量加法和乘以標量的規則適用於一組元素，則稱它們定義了向量空間。

線性組合和線性相關

形式為

$q_{1}\mathbf {a_{1}} +q_{2}\mathbf {a_{2}} +q_{3}\mathbf {a_{3}} +....+q_{m}\mathbf {a_{m}}$

被稱為向量的線性組合。

線上性組合中乘以標量的向量集被稱為向量的跨度。使用“跨度”一詞是因為標量 (q) 可以取任何值——這意味著向量空間中由跨度定義的任何子集都可以包含從該子集中得出的向量。

假設有一組向量 (${a_{1},a_{2},....,a_{m}}$)，如果可以使用任何線性組合將這些向量中的一個用其他向量表示出來，那麼這組向量被稱為線性相關。如果無法使用任何線性組合將這些向量中的任何一個用其他向量表示出來，則這組向量被稱為線性無關。

換句話說，如果標量存在這樣的值

(1). $\mathbf {a_{1}} =q_{2}\mathbf {a_{2}} +q_{3}\mathbf {a_{3}} +....+q_{m}\mathbf {a_{m}}$

該集合被稱為線性相關。

有一種方法可以確定線性相關性。從 (1) 可以看出，如果將 $q_{1}$ 設定為負一，那麼

$q_{1}\mathbf {a_{1}} +q_{2}\mathbf {a_{2}} +q_{3}\mathbf {a_{3}} +....+q_{m}\mathbf {a_{m}} =0$

因此，一般來說，如果一個線性組合可以寫成一個零向量的和，那麼向量集 ($\mathbf {a_{1},a_{2},....,a_{m}} )$ 不是線性無關的。

如果兩個向量是線性相關的，那麼它們位於同一條直線上（無論 a 和 b 在直線上哪裡，都可以找到標量來產生一個線性組合，該線性組合是一個零向量）。如果三個向量是線性相關的，那麼它們位於同一條直線上或同一個平面上（共線或共面）。

維度

如果向量空間中的 n+1 個向量是線性相關的，那麼 n 個向量是線性無關的，該空間被稱為具有 n 維。n 個向量集被稱為向量空間的基。

標量積

也稱為“點積”或“內積”。標量積是一種從向量之間的關係中消除角度度量問題的方法，正如韋爾所說，它是一種比較任意傾斜的向量的長度的方法。

考慮兩個具有公共原點的向量

$\mathbf {a}$ 在鄰邊的投影是

$P=|\mathbf {a} |cos\theta$

其中 $|\mathbf {a} |$ 是 $\mathbf {a}$ 的長度。

標量積定義為

(2) $\mathbf {a.b} =|\mathbf {a} ||\mathbf {b} |cos\theta$

注意，如果 $\mathbf {a}$ 和 $\mathbf {b}$ 垂直，則 $cos\theta$ 為零。這意味著如果標量積為零，那麼構成它的向量是正交的（相互垂直）。

(2) 還允許將 $cos\theta$ 定義為

$cos\theta =\mathbf {a.b} /(|\mathbf {a} ||\mathbf {b} |)$

標量積的定義還允許根據向量本身的概念定義向量的長度。向量與其自身的標量積是

$\mathbf {a.a} =|\mathbf {a} ||\mathbf {a} |cos0$

cos 0（零的餘弦）為 1，因此

$\mathbf {a.a} =a^{2}$

這是我們第一個關於向量和標量之間的直接關係。這可以表示為

(3) $a={\sqrt {\mathbf {a.a} }}$

其中 a 是 $\mathbf {a}$ 的長度。

性質

1. 線性 $[G\mathbf {a} +H\mathbf {b} ].\mathbf {c} =G\mathbf {a.c} +H\mathbf {b.c}$

2. 對稱性 $\mathbf {a.b} =\mathbf {b.a}$

3. 正定性 $\mathbf {a.a}$ 大於或等於 0

4. 對向量加法的分配律 $\mathbf {(a+b).c} =\mathbf {a.c+b.c}$

5. 施瓦茨不等式 $|\mathbf {a.b} |\leq ab$

6. 平行四邊形等式 $|\mathbf {a} +\mathbf {b} |^{2}+|\mathbf {a} -\mathbf {b} |^{2}=2(|\mathbf {a} |^{2}+|\mathbf {b} |^{2})$

從向量物理學的角度來看，標量積最重要的性質是標量積用座標表示的表示式。

7. $\mathbf {a.b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

這根據座標表示了向量的長度（勾股定理）

8. $\mathbf {a.a} =a^{2}=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}$

公式 7 的推導如下：

$\mathbf {a} =a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k}$

其中 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 是沿著座標軸的單位向量。由 (4) 可知

$\mathbf {a.b} =(a_{1}\mathbf {i} +a_{2}\mathbf {j} +a_{3}\mathbf {k} ).\mathbf {b} =a_{1}\mathbf {i} .\mathbf {b} +a_{2}\mathbf {j} .\mathbf {b} +a_{3}\mathbf {k} .\mathbf {b}$

但 $\mathbf {b} =b_{1}\mathbf {i} +b_{2}\mathbf {j} +b_{3}\mathbf {k}$

所以

$\mathbf {a.b} =b_{1}a_{1}\mathbf {i.i} +b_{2}a_{1}\mathbf {i.j} +b_{3}a_{1}\mathbf {i.k} +b_{1}a_{2}\mathbf {j.i} +b_{2}a_{2}\mathbf {j.j} +b_{3}a_{2}\mathbf {j.k} +b_{1}a_{3}\mathbf {k.i} +b_{2}a_{3}\mathbf {k.j} +b_{3}a_{3}\mathbf {k.k}$

$\mathbf {i.j,i.k,j.k,}$ 等等都為零，因為向量是正交的，還有 $\mathbf {i.i,j.j}$ 和 $\mathbf {k.k}$ 都為 1（這些都是定義為長度為 1 個單位的單位向量）。

利用這些結果

$\mathbf {a.b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

矩陣

矩陣是按矩形排列的一組數字。它們線上性代數中尤為重要，因為它們可以用來表示線性方程的元素。

11a + 2b = c

5a + 7b = d

上述方程中的常數可以用矩陣表示

$\mathbf {A} ={\begin{bmatrix}11&2\\5&7\\\end{bmatrix}}$

矩陣的元素通常用小寫字母符號表示

$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{bmatrix}}$

如果所有對應的元素相等，則稱矩陣相等。

例如：如果 $a_{ij}=b_{ij}$

那麼 $\mathbf {A} =\mathbf {B}$

矩陣加法

矩陣加法是透過將一個矩陣的各個元素加到另一個矩陣的對應元素來實現的。

$c_{ij}=a_{ij}+b_{ij}$

或 $\mathbf {C} =\mathbf {A} +\mathbf {B}$

矩陣加法具有以下性質

1. 交換律 $\mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A}$

2. 結合律 $(\mathbf {A} +\mathbf {B} )+\mathbf {C} =\mathbf {A} +(\mathbf {B} +\mathbf {C} )$

和

3. $\mathbf {A} +(-\mathbf {A} )=0$

4. $\mathbf {A} +0=\mathbf {A}$

從矩陣加法可以看出，矩陣 $\mathbf {A}$ 和數字 p 的乘積就是 $p\mathbf {A}$，其中矩陣的每個元素都分別乘以 p。

矩陣的轉置

當矩陣的行和列互換時，矩陣就被轉置了。

$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}$

$\mathbf {A^{T}} ={\begin{bmatrix}a_{11}&a_{21}&a_{31}\\a_{12}&a_{22}&a_{32}\\a_{13}&a_{23}&a_{33}\\\end{bmatrix}}$

注意，主對角線元素在轉置後保持不變。

如果矩陣等於其轉置，則該矩陣是對稱的，例如：$a_{kj}=a_{jk}$.

如果 $\mathbf {A^{T}} =-\mathbf {A}$，則該矩陣是反對稱的，例如：$a_{kj}=-a_{jk}$。反對稱矩陣的主對角線由元素為零的元素組成。

其他型別的矩陣

對角矩陣：主對角線以上和以下的所有元素均為零。

${\begin{bmatrix}4&0&0\\0&-1&0\\0&0&2\\\end{bmatrix}}$

單位矩陣：用 I 表示，是對角矩陣，其中主對角線的所有元素均為 1。

${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}}$

矩陣乘法

矩陣乘法是根據確定線性變換系數的問題來定義的。

考慮兩個座標系之間的線性變換集，這些座標系共享一個共同的原點，並且透過座標軸的旋轉相互關聯。

兩個座標系相對於彼此旋轉

如果有三個座標系 x、y 和 z，它們可以從一個座標系變換到另一個座標系

$x_{1}=a_{11}y_{1}+a_{12}y_{2}$

$x_{2}=a_{21}y_{1}+a_{22}y_{2}$

$y_{1}=b_{11}z_{1}+b_{12}z_{2}$

$y_{2}=b_{21}z_{1}+b_{22}z_{2}$

$x_{1}=c_{11}z_{1}+c_{12}z_{2}$

$x_{2}=c_{21}z_{1}+c_{22}z_{2}$

透過替換

$x_{1}=a_{11}(b_{11}z_{1}+b_{12}z_{2})+a_{12}(b_{21}z_{1}+b_{22}z_{2})$

$x_{2}=a_{21}(b_{11}z_{1}+b_{12}z_{2})+a_{22}(b_{21}z_{1}+b_{22}z_{2})$

$x_{1}=(a_{11}b_{11}+a_{12}(b_{21})z_{1}+(a_{11}b_{12}+a_{12}b_{22})z_{2}$

$x_{2}=(a_{21}b_{11}+a_{22}(b_{21})z_{1}+(a_{21}b_{12}+a_{22}b_{22})z_{2}$

因此

$c_{11}=(a_{11}b_{11}+a_{12}(b_{21})$

$c_{12}=(a_{11}b_{12}+a_{12}b_{22})$

$c_{21}=(a_{21}b_{11}+a_{22}b_{21})$

$c_{22}=(a_{21}b_{12}+a_{22}b_{22})$

係數矩陣為

$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}$

$\mathbf {B} ={\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}}$

$\mathbf {C} ={\begin{bmatrix}c_{11}&c_{12}\\c_{21}&c_{22}\end{bmatrix}}$

從線性變換中，A 和 B 的乘積定義為

$\mathbf {C} =\mathbf {AB} ={\begin{bmatrix}(a_{11}b_{11}+a_{12}b_{21})&(a_{11}b_{12}+a_{12}b_{22})\\(a_{21}b_{11}+a_{22}b_{21})&(a_{21}b_{12}+a_{22}b_{22})\end{bmatrix}}$

在討論標量積時，我們發現，對於一個平面，標量積的計算方式為：$\mathbf {a.b} =a_{1}b_{1}+a_{2}b_{2}$，其中 a 和 b 是向量 a 和 b 的座標。

現在，數學家將矩陣的行和列定義為向量。

列向量為 $\mathbf {b} ={\begin{bmatrix}b_{11}\\b_{21}\end{bmatrix}}$

行向量為 $\mathbf {a} ={\begin{bmatrix}a_{11}&a_{12}\end{bmatrix}}$

矩陣可以被描述為向量，例如

$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}={\begin{bmatrix}\mathbf {a_{1}} \\\mathbf {a_{2}} \end{bmatrix}}$

和

$\mathbf {B} ={\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}}={\begin{bmatrix}\mathbf {b_{1}} \mathbf {b_{2}} \end{bmatrix}}$

矩陣乘法定義為向量之間的標量積，因此

$\mathbf {C} ={\begin{bmatrix}\mathbf {a_{1}.b_{1}} &\mathbf {a_{1}.b_{2}} \\\mathbf {a_{2}.b_{1}} &\mathbf {a_{2}.b_{2}} \end{bmatrix}}$

根據標量積的定義， $\mathbf {a_{1}.b_{1}} =a_{11}b_{11}+a_{12}b_{21}$ 等等。

在一般情況下

$\mathbf {C} ={\begin{bmatrix}\mathbf {a_{1}.b_{1}} &\mathbf {a_{1}.b_{2}} &.&\mathbf {a_{1}.b_{n}} \\\mathbf {a_{2}.b_{1}} &\mathbf {a_{2}.b_{2}} &.&\mathbf {a_{2}.b_{n}} \\.&.&.&.\\\mathbf {a_{m}.b_{1}} &\mathbf {a_{m}.b_{2}} &.&\mathbf {a_{m}.b_{n}} \end{bmatrix}}$

這被稱為行乘以列的乘法（例如：行向量乘以列向量）。第一個矩陣的列數必須與第二個矩陣的行數相同，否則乘法未定義。

矩陣乘法後，乘積矩陣的行數與第一個矩陣相同，列數與第二個矩陣相同。

${\begin{bmatrix}1&3&4\\6&3&2\end{bmatrix}}$ 乘以 ${\begin{bmatrix}2\\3\\7\end{bmatrix}}$ 有 2 行 1 列 ${\begin{bmatrix}39\\35\end{bmatrix}}$

例如：第一行是$1*2+3*3+4*7=39$，第二行是$6*2+3*3+2*7=35$

$\mathbf {AB} ={\begin{bmatrix}1&3&2\\2&-1&3\end{bmatrix}}$ 乘以 ${\begin{bmatrix}2&3&4\\3&2&1\\5&1&3\end{bmatrix}}$ 有2行和3列，得到的結果是${\begin{bmatrix}21&11&13\\16&7&16\end{bmatrix}}$

注意，$\mathbf {BA}$ 無法計算，因為要進行矩陣乘法， **第一個矩陣的列數必須等於第二個矩陣的行數。**

矩陣乘法的性質

1. 不滿足交換律 $\mathbf {AB} \neq \mathbf {BA}$

2. 滿足結合律 $\mathbf {A(BC)} =\mathbf {(AB)C}$

$(k\mathbf {A} )\mathbf {B} =k(\mathbf {AB} )=\mathbf {A} (k\mathbf {B} )$

3. 滿足對矩陣加法的分配律

$(\mathbf {A} +\mathbf {B} )\mathbf {C} =\mathbf {AC} +\mathbf {BC}$

矩陣乘法不滿足交換律，因此$\mathbf {C} (\mathbf {A} +\mathbf {B} )=\mathbf {CA} +\mathbf {CB}$ 是一個單獨的情況。

4. 消去律不總是成立

$\mathbf {AB} =0$ 不意味著 $\mathbf {A} =0$ 或者 $\mathbf {B} =0$

矩陣乘法存在一種交換律。這涉及到主對角線上的值都相等的標量矩陣。例如

$\mathbf {S} ={\begin{bmatrix}k&0&0\\0&k&0\\0&0&k\end{bmatrix}}$

在這種情況下，$\mathbf {AS} =\mathbf {SA} =k\mathbf {A}$。如果標量矩陣是單位矩陣: $\mathbf {AI} =\mathbf {IA} =\mathbf {A}$.

線性變換

一個簡單的線性變換，例如

$x_{1}=a_{11}y_{1}+a_{12}y_{2}$

$x_{2}=a_{21}y_{1}+a_{22}y_{2}$

可以表示為

$\mathbf {x} =\mathbf {Ay}$

例如

${\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}*{\begin{bmatrix}y_{1}\\y_{2}\end{bmatrix}}$

和 $y_{1}=b_{11}z_{1}+b_{12}z_{2}$

$y_{2}=b_{21}z_{1}+b_{22}z_{2}$

作為： $\mathbf {y} =\mathbf {Bz}$

使用結合律

$\mathbf {x} =\mathbf {A} (\mathbf {Bz} )=\mathbf {ABz} =\mathbf {Cz}$

因此

$\mathbf {C} =\mathbf {AB} ={\begin{bmatrix}(a_{11}b_{11}+a_{12}b_{21})&(a_{11}b_{12}+a_{12}b_{22})\\(a_{21}b_{11}+a_{22}b_{21})&(a_{21}b_{12}+a_{22}b_{22})\end{bmatrix}}$

如前所述。

指標符號

考慮一個簡單的座標旋轉

$x^{\mu }$ 被定義為 $x_{1}$ , $x_{2}$

$x^{\nu }$ 被定義為 $x_{1}^{'}$ , $x_{2}^{'}$

標量積可以寫成

$\mathbf {s.s} =g_{\mu \nu }x^{\mu }x^{\nu }$

其中

$g_{\mu \nu }={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$

被稱為這個二維空間的度量張量。

$\mathbf {s.s} =g_{11}x_{1}x_{1}^{'}+g_{12}x_{1}x_{2}^{'}+g_{21}x_{2}x_{1}^{'}+g_{22}x_{2}x_{2}^{'}$

現在，$g_{11}=1$, $g_{12}=0$, $g_{21}=0$, $g_{22}=1$ 所以

$\mathbf {s.s} =x_{1}x_{1}^{'}+x_{2}x_{2}^{'}$

如果沒有座標旋轉，標量積是

$\mathbf {s.s} =x_{1}x_{1}+x_{2}x_{2}$

$s^{2}=x_{1}^{2}+x_{2}^{2}$

這就是勾股定理。

求和約定

作為下標和上標出現的索引將被求和。

$g_{\mu \nu }x^{\mu }x^{\nu }=g_{11}x_{1}x_{1}^{'}+g_{12}x_{1}x_{2}^{'}+g_{21}x_{2}x_{1}^{'}+g_{22}x_{2}x_{2}^{'}$

透過將$\nu$提升為上標，它將被從求和中移除，即：。

$g_{\mu }^{\nu }x^{\mu }x^{\nu }=g_{1\nu }x_{1}x_{\nu }^{'}+g_{2\nu }x_{2}x_{\nu }^{'}$

索引表示法中的矩陣乘法

考慮

列乘以行

${\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}$ 乘以 ${\begin{bmatrix}y_{1}&y_{2}\end{bmatrix}}$ = ${\begin{bmatrix}x_{1}y_{1}&x_{1}y_{2}\\x_{2}y_{1}&x_{2}y_{2}\end{bmatrix}}$

矩陣乘積$\mathbf {XY} =x_{i}y_{j}$ 其中 i = 1, 2 j = 1, 2

由於沒有求和，因此索引都是下標。

行乘以列: ${\begin{bmatrix}x_{1}&x_{2}\end{bmatrix}}$ 乘以 ${\begin{bmatrix}y_{1}\\y_{2}\end{bmatrix}}$ = ${\begin{bmatrix}x_{1}y_{1}&x_{2}y_{2}\end{bmatrix}}$

矩陣乘積 $\mathbf {XY} =\delta _{ij}x^{i}y^{j}$

其中 $\delta _{ij}$ 被稱為克羅內克δ，當 $i\neq j$ 時值為 0，當 $i=j$ 時值為 1。它等同於單位矩陣的指標表示。

${\begin{bmatrix}1&0\\0&1\end{bmatrix}}$

在求和時，一個i值是下標，另一個是上標。

一般來說，矩陣可以用以下任意一種表示：

$M_{i}^{j}$ , $M_{ij}$ , $M_{j}^{i}$ , $M^{ij}$，取決於哪個下標或上標正在求和。

指標表示中的向量

向量可以表示為基向量的線性組合。

$\mathbf {x} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3}$

在指標表示中，它表示為：$x=a^{i}e_{i}$

指標表示中的線性變換

考慮 $\mathbf {x} =\mathbf {Ay}$，其中 $\mathbf {A}$ 是係數矩陣，$\mathbf {x}$ 和 $\mathbf {y}$ 是座標矩陣。

用指標表示法，這可以寫成

$x^{\mu }=A_{\nu }^{\mu }x^{\nu }$

這可以寫成

$x_{1}=a_{11}x_{1}^{'}+a_{12}x_{2}^{'}+a_{13}x_{3}^{'}$

$x_{2}=a_{21}x_{1}^{'}+a_{22}x_{2}^{'}+a_{23}x_{3}^{'}$

$x_{3}=a_{31}x_{1}^{'}+a_{32}x_{2}^{'}+a_{33}x_{3}^{'}$

用指標表示法的標量積

用指標表示法，標量積為

$\mathbf {x.y} =\delta _{ij}x^{i}y^{j}$

分析曲面和變換

在19世紀初，人們發現諸如歐幾里得平行公設等問題需要發展一種新的幾何學型別，這種幾何學可以處理曲面以及實數和虛數平面。這種方法的基礎是高斯對曲面的分析，它使我們能夠使用各種座標系和位移在任何型別的曲面上進行運算。

基礎幾何分析作為狹義相對論的入門很有用，因為它暗示了座標變換中出現的係數的物理意義。

假設曲面上有一條線。這條線的長度可以用座標系來表示。二維空間中的一小段線 $\Delta s$ 可以用勾股定理表示為

$\Delta s^{2}=\Delta x^{2}+\Delta y^{2}$

假設曲面上還有另一個座標系，有兩個軸：x₁, x₂，如何用這些座標表示線的長度？高斯解決了這個問題，對於兩個座標軸，他的分析非常簡單明瞭

圖1

可以使用基礎微分幾何來描述平面上的位移，這些位移與曲面上的位移有關

$\Delta Y=\Delta x_{1}{\frac {\delta Y}{\delta x_{1}}}+\Delta x_{2}{\frac {\delta Y}{\delta x_{2}}}$

$\Delta Z=\Delta x_{1}{\frac {\delta Z}{\delta x_{1}}}+\Delta x_{2}{\frac {\delta Z}{\delta x_{2}}}$

然後假設短線的位移由一個公式給出，該公式被稱為度量，例如勾股定理

$\Delta S^{2}=\Delta Y^{2}+\Delta Z^{2}$

然後可以將 $\Delta Y$ 和 $\Delta Z$ 的值代入該度量

$\Delta S^{2}=(\Delta x_{1}{\frac {\delta Y}{\delta x_{1}}}+\Delta x_{2}{\frac {\delta Y}{\delta x_{2}}})^{2}+(\Delta x_{1}{\frac {\delta Z}{\delta x_{1}}}+\Delta x_{2}{\frac {\delta Z}{\delta x_{2}}})^{2}$

展開後，得到以下結果

$\Delta S^{2}=$

$({\frac {\delta Y}{\delta x_{1}}}{\frac {\delta Y}{\delta x_{1}}}+{\frac {\delta Z}{\delta x_{1}}}{\frac {\delta Z}{\delta x_{1}}})\Delta x_{1}\Delta x_{1}$

$+({\frac {\delta Y}{\delta x_{2}}}{\frac {\delta Y}{\delta x_{1}}}+{\frac {\delta Z}{\delta x_{2}}}{\frac {\delta Z}{\delta x_{1}}})\Delta x_{2}\Delta x_{1}$

$+({\frac {\delta Y}{\delta x_{1}}}{\frac {\delta Y}{\delta x_{2}}}+{\frac {\delta Z}{\delta x_{1}}}{\frac {\delta Z}{\delta x_{2}}})\Delta x_{1}\Delta x_{2}$

$+({\frac {\delta Y}{\delta x_{2}}}{\frac {\delta Y}{\delta x_{2}}}+{\frac {\delta Z}{\delta x_{2}}}{\frac {\delta Z}{\delta x_{2}}})\Delta x_{2}\Delta x_{2}$

這可以用求和符號表示

$\Delta S^{2}=\sum _{i=1}^{2}\sum _{k=1}^{2}({\frac {\delta Y}{\delta x_{i}}}{\frac {\delta Y}{\delta x_{k}}}+{\frac {\delta Z}{\delta x_{i}}}{\frac {\delta Z}{\delta x_{k}}})\Delta x_{i}\Delta x_{k}$

或者，使用指標表示法

$\Delta S^{2}=g_{ik}\Delta x^{i}\Delta x^{k}$

其中

$g_{ik}=({\frac {\delta Y}{\delta x^{i}}}{\frac {\delta Y}{\delta x^{k}}}+{\frac {\delta Z}{\delta x^{i}}}{\frac {\delta Z}{\delta x^{k}}})$

如果座標沒有合併，則 $\Delta s$ 依賴於兩組座標。用矩陣表示法

$\Delta s^{2}=\mathbf {g} \Delta \mathbf {x} \Delta \mathbf {x}$

變成

${\begin{bmatrix}\Delta x_{1}&\Delta x_{2}\end{bmatrix}}$ 乘以 ${\begin{bmatrix}a&b\\c&d\end{bmatrix}}$ 乘以 ${\begin{bmatrix}\Delta x_{1}\\\Delta x_{2}\end{bmatrix}}$

其中 a、b、c、d 代表 $g_{ik}$ 的值。

因此

${\begin{bmatrix}\Delta x_{1}a+\Delta x_{2}c&\Delta x_{1}b+\Delta x_{2}d\end{bmatrix}}$ 乘以 ${\begin{bmatrix}\Delta x_{1}\\\Delta x_{2}\end{bmatrix}}$

結果是

$(\Delta {x_{1}}a+\Delta {x_{2}}c)\Delta {x_{1}}+(\Delta {x_{1}}b+\Delta {x_{2}}d)\Delta {x_{2}}=\Delta {x_{1}}^{2}a+2\Delta {x_{1}}\Delta {x_{2}}(c+b)+\Delta {x_{2}}^{2}d$

因此

$\Delta {s}^{2}=\Delta {x_{1}}^{2}a+2\Delta {x_{1}}\Delta {x_{2}}(c+b)+\Delta {x_{2}}^{2}d$

$\Delta {s}^{2}$ 是一個**雙線性形式**，它取決於 $\Delta {x_{1}}$ 和 $\Delta {x_{2}}$。它可以用矩陣表示法寫成

$\Delta {s}^{2}=\mathbf {\Delta {x}^{T}A\Delta {x}}$

其中 A 是一個包含 $g_{ik}$ 值的矩陣。 這是一個被稱為二次形式的雙線性形式的特殊情況，因為同一個矩陣 ($\mathbf {\Delta {x}}$) 出現了兩次；在廣義雙線性形式 $\mathbf {B} =\mathbf {x^{T}Ay}$ 中（矩陣 $\mathbf {x}$ 和 $\mathbf {y}$ 是不同的）。

如果曲面是歐幾里得平面，則 gik 的值是

${\begin{bmatrix}\delta {Y}/\delta {x_{1}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{1}}\delta {Z}/\delta {x_{1}}&\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{1}}\\\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{1}}&\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{2}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{2}}\end{bmatrix}}$

這變成

$g_{\mu \nu }={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$

所以矩陣 A 是單位矩陣 I，並且

$\Delta {s}^{2}=\mathbf {\Delta {x^{T}}I\Delta {x}}$

和

$\Delta {s}^{2}=\Delta {x_{1}}^{2}+\Delta {x_{2}}^{2}$

再次得到了勾股定理。

如果曲面是從其他度量（例如 $\Delta {s^{2}}=-\Delta {Y}^{2}+\Delta {Z}^{2}$）推匯出來的，則 gik 的值是

${\begin{bmatrix}-\delta {Y}/\delta {x_{1}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{1}}\delta {Z}/\delta {x_{1}}&-\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{1}}\\-\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{1}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{1}}&-\delta {Y}/\delta {x_{2}}\delta {Y}/\delta {x_{2}}+\delta {Z}/\delta {x_{2}}\delta {Z}/\delta {x_{2}}\end{bmatrix}}$

變成

$g_{\mu \nu }={\begin{bmatrix}-1&0\\0&1\end{bmatrix}}$

這允許原始度量被恢復，即： $\Delta {s^{2}}=-\Delta {x_{1}}^{2}+\Delta {x_{2}}^{2}$.

有趣的是，將幾何分析與矩陣代數的變換進行比較，矩陣代數的變換是在上面關於指標符號的部分推匯出來的

$\mathbf {s.s} =g_{11}x_{1}x_{1}^{'}+g_{12}x_{1}x_{2}^{'}+g_{21}x_{2}x_{1}^{'}+g_{22}x_{2}x_{2}^{'}$

現在，

$g_{\mu \nu }={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$

即： $g_{11}=1$，$g_{12}=0$，$g_{21}=0$，$g_{22}=1$ 所以

$\mathbf {s.s} =x_{1}x_{1}^{'}+x_{2}x_{2}^{'}$

如果沒有座標旋轉，標量積是

$\mathbf {s.s} =x_{1}x_{1}+x_{2}x_{2}$

$s^{2}=x_{1}^{2}+x_{2}^{2}$

這恢復了勾股定理。然而，讀者可能已經注意到，勾股定理在標量積的推導中一開始就被假設了（見上文）。

幾何分析表明，如果假設了度量並且允許微分幾何的條件存在，那麼可以從另一個座標系中推匯出一個座標系。這種分析也可以使用矩陣代數來進行，前提是相同的假設。

上面的例子使用了簡單的二維勾股度量，一些其他的度量，比如四維閔可夫斯基空間的度量

$\Delta S^{2}=-\Delta T^{2}+\Delta X^{2}+\Delta Y^{2}+\Delta Z^{2}$

可以用來代替勾股定理。