狹義相對論/同時性、時間膨脹和長度收縮

狹義相對論

關於同時性的相對性的更多資訊

大多數物理理論假設可以同步時鐘。如果您在一個空間體積內設定一個同步時鐘陣列，並同時對其進行快照，您會發現最靠近您的時鐘顯示的時間比其他時鐘晚，這是由於光從每個遙遠的時鐘傳播到您需要時間。但是，如果已知正確的時鐘位置，透過考慮光的傳輸時間，可以很容易地補償這些差異並正確同步時鐘。同步時鐘的可能性存在於光速是恆定的，並且這個恆定速度可以用於同步過程（使用可預測的延遲，當光用於同步時鐘時，被稱為“愛因斯坦同步”）。

時間上的洛倫茲變換比較了任何時刻同步時鐘的讀數。它比較了時鐘上的實際讀數，考慮了觀察者之間傳輸資訊所需的任何時間延遲，並回答了“另一個觀察者的時鐘現在，在這個時刻，實際讀數是多少”的問題。這個問題的答案令人震驚。時間上的洛倫茲變換表明，任何相對於您移動的參考系中的時鐘都停止同步！

相對運動觀察者之間的不同步在下面用一個更簡單的圖表說明。

同時性的相對性的影響是讓每個觀察者認為一組不同的事件是同時發生的。時鐘之間的相對論相位差（“相對論相位”）意味著相對於彼此移動的觀察者具有不同的同時發生事件集，或者是在他們的“現在時刻”。正是這種時間不再是絕對的發現深深地困擾了許多相對論的學生。

時鐘在兩個觀察者之間相差多少取決於時鐘到觀察者的距離（ $t=xv/c^{2}$ ）。請注意，如果兩個觀察者都是慣性參考系的一部分，並且時鐘在空間的每個點都同步，那麼可以透過簡單地讀取遠處點的時鐘和原點時鐘之間的差來獲得相位差。這種差異對兩個觀察者來說都具有相同的值。

示例：閃爍的燈光

兩個相對於彼此靜止的燈光相隔 3000 米。這些燈光一個接一個地閃爍，閃爍之間的時間間隔為 4 微秒。你需要以多快的速度沿著燈光的線移動才能看到燈光同時閃爍？

這個問題是相對論相位的直接例子，對於運動的觀察者來說是同時發生的事件，在他們自己的參考系中是連續的事件。具有距離的時鐘之間的相位差由下式給出

$\Delta t=vx/c^{2}$

所以 $v=\Delta tc^{2}/x$

除以 $c$ 將 $v$ 表示為光速的一部分，得到

$v_{c}=\Delta tc/x$

因此： $v_{c}={\frac {4\times 10^{-6}\times 3\times 10^{8}}{3\times 10^{3}}}$

因此 $v_{c}=0.4c$

（參見 Scherr 等人 (2001) 中的“爆炸”示例）

討論示例中靜止觀察者和運動觀察者對閃光的時間分配之間的關係：事件時間的洛倫茲變換為 $t'=\gamma (t-vx/c^{2})$ ，它由經過時間 $t$ 和相位差 $vx/c^{2}$ 組成。閃光燈示例的安排是，當兩個慣性參考系中的觀察者在第一次閃光時彼此相遇時， $t=t'=0$ ，並且 $t=t$ 和 $t'=0$ 是第二次閃光的時間。

如果 $t'=0$ ，那麼 $0=\gamma (t-vx/c^{2})$ ，因此，根據洛倫茲變換，當 $t=vx/c^{2}$ 時，運動觀察者發現事件在靜止慣性參考系中是同時發生的，即：當靜止參考系中的經過時間等於兩個參考系之間的相位差時。

Scherr, R.E., Shaffer, P.S. and Vokos, S. 學生對狹義相對論中的時間理解：同時性和參考系。物理教育研究，美國物理學雜誌增刊，69，S24-35（2001）

示例：相對論捕蟲

一艘 1000 米長的宇宙飛船需要以多快的速度航行才能觀察到與它船首和船尾對齊的靜止時鐘之間存在納秒級的差異？

從 $t=xv/c^{2}$

$10^{-9}=10^{3}v/(9\times 10^{16})$

因此 $v=9\times 10^{4}ms^{-1}$ 或每秒 90 公里。

這種效應可用於將他們在自身慣性參考系中是雙胞胎的不同年齡的蟲子聚集在一起。

比爾駕駛著一艘非常長的宇宙飛船經過吉姆，並同時捕捉到兩隻蟲子，一隻與宇宙飛船的船首重合，一隻與船尾重合。儘管這些蟲子在它們自身的參考系中是雙胞胎，但它們在比爾的參考系中年齡不同。被捕的蟲子可以自由地在比爾的宇宙飛船上下游蕩，並且可以相遇。

以每秒 90 公里速度航行的宇宙飛船需要多長的長度才能捕捉到圖片中的蟲子？

仙女座悖論

當我們說事件正在“現在”發生時，我們指的是什麼？如果我們正在俯瞰城市景觀，觀察交通情況，很多事情似乎都在同時發生。我們可以用相機拍一張快照，照片上的場景包含了所有幾乎同時發生的事情。它們只是“幾乎”在同一時間發生，因為照片上最遠處的事件實際上比附近的事件發生得稍早，因為光到達相機需要時間。如果我們想要發現真正同時發生的事件，我們需要減去光到達我們的時間。如果你正在觀察月球上的事件，這將是非常必要的：如果你在地球上看到月球鐘上的時間，你會知道月球上的實際時間要晚一秒多。但這夠了嗎？由於運動導致的時鐘之間的相對論相位差怎麼辦？

狹義相對論除了光傳播時間之外，還引入了一個因素，它擾亂了我們對哪些事件是同時發生的認識。時鐘之間的相對論相位差在月球距離處很小，但在與附近星系一樣大的距離處卻產生了驚人的結果，即，在地球上駕駛的觀察者與站在地球上的另一個人相比，他們可能具有完全不同的事件集與他們的“現在時刻”同時發生。這種相對論相位效應的經典示例是“仙女座悖論”，也稱為“Rietdijk-Putnam-Penrose”論證。彭羅斯描述了這個論證：

“兩個人在街上相遇；根據其中一個人，仙女座星際艦隊已經出發了，而對另一個人來說，決定是否真正開始旅程尚未做出。為什麼關於那個決定的結果還存在一些不確定性？如果對任何一個人來說，決定已經做出，那麼肯定不會有任何不確定性。太空艦隊的發射是不可避免的。”（彭羅斯 1989）。

下面的圖示說明了這個論點。

請注意，這兩位觀察者實際上都無法“看到”現在仙女座上發生的事情。爭論的焦點不是關於什麼可以“看到”，而是關於不同的觀察者認為他們的瞬時現在時刻包含了什麼。這兩位觀察者在望遠鏡中觀察到相同的，兩百萬年前的事件，但運動的觀察者必須假設仙女座上現在的事件比靜止的觀察者的現在時刻早一兩天。（順便說一下，這兩位觀察者在望遠鏡中看到相同的事件，因為從地球到仙女座的距離的長度收縮正好抵消了仙女座上的時間差。）

這個“悖論”引發了關於時間和自由意志本質的相當多的哲學辯論。本書的進階內容討論了圍繞這種狹義相對論的幾何解釋的一些問題。

同時性相對論的一個結果是，如果汽車司機發射一枚太空火箭飛往仙女座星系，它可能比從地面發射的太空火箭早出發幾天。這是因為對於正在移動的汽車司機來說，與地面上的現在時刻相比，隨著距離的增加，他們的“現在時刻”也逐漸提前。下圖顯示了汽車司機的現在時刻。

仙女座悖論的最終效果是，當一個人向一個遙遠的地方移動時，那個地方的事件比沒有向那個遙遠的地方移動的人的事件發生得晚。兩個人現在時刻的事件之間存在一個時間間隔。

雙生子悖論

“雙生子悖論”來源於朗之萬（1911 年）的一篇文章，他在文章中用前往遙遠恆星再返回的旅行來描述不同慣性參考系中的時間關係。朗之萬最初的例子被稱為“時鐘悖論”，它表明，一個前往遙遠恆星再返回的太空旅行者發現，他的衰老程度比留在地球上的人要少。Benguigui（2012 年）詳細描述了隨著時間的推移，這個例子是如何演變成兩個雙胞胎的故事，一個進入太空旅行，一個留在家裡，以及韋爾（1922 年）如何將它描述為“雙生子悖論”。“雙生子悖論”是同時性相對論和時間膨脹的一個有趣的例子，值得仔細研究，以便理解狹義相對論的這些特徵。但是請注意，“雙生子悖論”之所以引起如此多的困惑，是因為雖然表面上看起來很簡單，但分析各個慣性參考系卻很複雜。

單程旅行

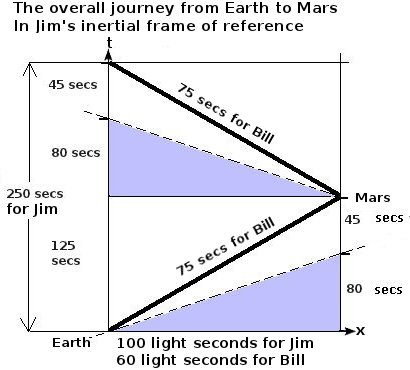
雙生子“悖論”包括兩個旅程，一個外向旅程和一個返回旅程。透過考慮沒有返回的只是外向旅程，可以學到很多關於同時性相對論的知識。單程旅行，沒有返回，可能包括以下場景：吉姆留在地球上，比爾乘坐宇宙飛船離開，比爾以 0.8c 的速度飛過吉姆，他們都在相遇時將自己的時鐘設定為零，比爾直飛火星，在那裡他放下一個記錄了他時鐘讀數的東西。留在地球上的吉姆發現，比爾在旅途中的時鐘記錄的時間比他自己的時間少。

前往火星的旅程包括兩個慣性參考系。在吉姆的參考系中，比爾在移動，吉姆是靜止的。在比爾的參考系中，吉姆、地球和火星在移動，比爾是靜止的。只有兩個參考系，所以諸如“如果吉姆認為自己正在移動，他會觀察到什麼”之類的問題等同於問“吉姆在比爾的參考系中如何移動？”。

旅程的開始如下所示

為了便於計算，假設火星距離地球 100 光秒。吉姆對旅程的看法很簡單，如下所示

如果火星距離 100 光秒，吉姆會計時比爾的旅程需要 125 秒 ( $100/0.8$ )。相對論時間膨脹會導致比爾的時鐘讀數為 75 秒，即

比爾的時鐘讀數將為： $125/\gamma$

其中伽馬為： ${\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=1.667$

所以 $125/1.6667=75$ 秒。

在吉姆的慣性參考系中，當比爾到達火星時，吉姆已經衰老了 125 秒，但由於時間膨脹，比爾只衰老了 75 秒。

比爾的這種沒有衰老的原因看起來很像悖論，因為人們可能會認為吉姆也應該比比爾衰老得少，畢竟，吉姆遠離比爾的程度與比爾遠離吉姆的程度一樣，所以比爾應該發現吉姆比自己衰老得少，就像吉姆發現比爾比自己衰老得少一樣。事實上，這裡沒有悖論，因為比爾和吉姆對旅程的理解非常不同。比爾對旅程的看法如下所示。

由於相對論相位，比爾發現火星上的時鐘比他自己的時鐘提前了 80 秒。火星時鐘在旅程中又記錄了 45 秒。45 秒的旅程時間是比爾在考慮時間膨脹後的預期時間（即： $75/\gamma =75/1.6667=45$ 秒）。更令人驚訝的是，當比爾考慮地球上吉姆的時鐘讀數時，他發現在地球上吉姆的時鐘在旅程中只過去了 45 秒，因為 80 秒的相對論相位差意味著，當比爾經過火星時，他的時鐘與地球上發生的事情是同時的，而地球上發生的事件只比他經過地球晚 45 秒。

如果比爾有一艘非常長的火箭，他可以使用“相對論捕蟲”的變體（見上文）來捕捉吉姆的一隻時鐘，就在比爾到達火星的瞬間。然後比爾可以證明在地球上有一個吉姆，他的時鐘在比爾的慣性參考系中只過去了 45 秒。如果比爾捕捉了吉姆的一隻時鐘，那個與比爾經過火星的時刻在他的自己的參考系中是同時的吉姆會記得，一艘宇宙飛船的尾部有一張巨大的網落下，在比爾經過他 45 秒後，網抓住了他的時鐘。

請注意，在這個故事中有兩個吉姆，一個與比爾訪問的火星同時，另一個與比爾在比爾的參考系中同時。與比爾在比爾的參考系中同時的那個吉姆，比那個與比爾到達時火星在他自己的參考系中同時的吉姆要早。

單程旅行是對稱的，因為吉姆觀察到比爾在旅途中的衰老程度比自己少，比爾也觀察到一個更早的吉姆比自己衰老程度少。

如果比爾繼續經過火星，直到他的時鐘顯示經過了 125 秒，那麼單程旅行將變得完全對稱，這時他會評估吉姆經歷了 75 秒的經過時間。當吉姆的時鐘顯示 125 秒時，吉姆發現比爾的時鐘顯示 75 秒，對稱地，當比爾的時鐘顯示 125 秒時，比爾發現吉姆的時鐘顯示 75 秒。這種對稱性在下圖的示意圖中得到了強調，該圖比較了吉姆和比爾的時鐘讀數。

速度變化時會發生什麼？

在上一節中，我們已經證明，當觀察者以恆定速度分離時，時間膨脹是對稱的。這種對稱性體現在，在單程旅行中，吉姆觀察到比爾的時鐘變慢，而比爾也觀察到吉姆的時鐘變慢。觀察者之間的對稱性意味著，比爾可以把自己看成是靜止的，觀察吉姆離開，反之亦然。

比爾發現，有兩個吉姆在不同的時間參與了前往火星然後突然改變方向返回地球的旅程：它們在圖中標記為 A 和 C。第一個吉姆的時鐘顯示從比爾經過地球起已經過去了 45 秒，這是在比爾的參考系中與比爾同時經過火星的吉姆。第二個吉姆的時鐘顯示從遇到比爾起已經過去了 205 秒，這個吉姆在比爾的參考系中與比爾同時到達火星並以 -0.8c 的速度開始返回地球的旅程。

由於不存在一個與比爾在速度變化時同時存在的吉姆，這在狹義相對論中引入了不對稱性。比爾在火星轉向返回地球並不等同於地球轉向迎接比爾，因為直到比爾轉向之前，尚不清楚是哪個地球和哪個吉姆在進行旅程。首次提出旅行者離開並返回時變年輕的例子的朗之萬 (1911) 非常清楚地認識到這種不對稱性，並指出：“因此，不對稱性——由於只有旅行者，在他的旅程中途，經歷了改變其速度方向的加速度”。

在狹義相對論中，物理定律對慣性參考系中的每個觀察者來說都是相同的。慣性參考系可以是船上房間或整個城市的所有時鐘和測量棒，慣性參考系的關鍵特徵是時鐘和測量棒彼此靜止。運動的測量方式是，宇宙的其餘部分相對於觀察者的慣性參考系運動。在比爾前往火星並返回地球的例子中，有三個慣性參考系：吉姆、外向的比爾和內向的比爾。外向的比爾和內向的比爾之間隔著一段比爾轉向時速度變化的時期。這段速度變化時期也可以看作是比爾單一慣性參考系中的一個非慣性間斷，在此之後，比爾的時鐘和測量棒與宇宙中其他部分的關係發生了變化。

諸如“如果轉向後與比爾同時存在的吉姆把自己看成是朝比爾運動，他會如何看待事件？”這樣的問題實際上是關於內向的比爾的參考系。在吉姆自己的慣性參考系中，比爾只是去火星，轉身回來。吉姆總是把自己看成是靜止的，除非他的參考系透過經歷速度變化而變得非慣性，在這種情況下，吉姆會把自己看成是從一個靜止狀態移動到另一個與宇宙具有不同關係的靜止狀態。狹義相對論認為物理定律在所有慣性參考系中都是相同的，它並不認為所有運動都是相對的，即使在非慣性變化中也是如此。

與比爾到達火星時同時存在的吉姆和比爾開始返回地球旅程時同時存在的吉姆之間的時間間隔被稱為“時間間隔”。“雙生子佯謬”中的時間間隔包含了外向和內向階段差的總和，在本例中，時間間隔為 160 秒。

“雙生子佯謬”的時間間隔描述

一旦接受比爾和吉姆對旅程有截然不同的看法，這些看法就可以在“時間間隔”描述中總結出來。在這種描述中，比爾飛往火星並發現那裡的時鐘比他自己的時鐘顯示的時間晚。他轉身飛回地球，並意識到同時性的相對性意味著，對比爾來說，地球上的時鐘會向前跳躍，並且比火星上的時鐘超前，又出現了一個“時間間隔”。當比爾回到地球時，時間間隔和時間膨脹意味著地球上的人記錄了比他記錄的更多的時鐘滴答聲。

為了便於計算，假設比爾以驚人的速度 0.8c 朝向一個距離 100 光秒（約 3000 萬公里）的遙遠點運動。下面的插圖顯示了吉姆和比爾的觀察結果

從比爾的觀點來看，存在時間膨脹和相位效應。正是“相位”的附加因素解釋了為什麼，儘管時間膨脹對兩個觀察者都發生，但比爾在整個旅程中觀察到吉姆的時鐘上的讀數與吉姆相同。

總結使用該示例解釋“雙生子佯謬”的數學公式

吉姆觀察到的距離為 100 光秒，遙遠點在他的參考系中。根據吉姆的說法，比爾完成旅程所需的時間為

所需時間 = 距離 / 速度，因此根據吉姆的說法

t=100/0.8=125

秒

同樣根據吉姆的說法，時間膨脹應該影響比爾的時鐘上觀察到的時間

T=t\times {\sqrt {1-v^{2}/c^{2}}}

所以

T=125\times {\sqrt {1-0.8^{2}}}=75

秒

因此，對吉姆來說，往返行程需要 250 秒，比爾的時鐘顯示 150 秒。

比爾測量的距離為

X=x\times {\sqrt {1-v^{2}/c^{2}}}=100\times {\sqrt {1-0.8^{2}}}=60

光秒。

對比爾來說，需要

X/v=60/0.8=75

秒。

比爾觀察到吉姆的時鐘由於時間膨脹而顯得執行緩慢

t^{'}=T\times {\sqrt {1-v^{2}/c^{2}}}

所以

t^{'}=75\times {\sqrt {1-0.8^{2}}}=45

秒。

但也有一個時間差為 $vx/c^{2}=80$ 秒。

因此，對於比爾來說，吉姆的時鐘從起點到遠點記錄了 125 秒。這包括吉姆時鐘在轉向點經過的 45 秒，以及旅程開始時的 80 秒時間差。比爾觀察到，吉姆的時鐘在整個旅程中記錄了總計 250 秒，這與吉姆在自己的時鐘上觀察到的一樣。

進一步閱讀

Benguigui, L (2012). 兩對雙胞胎的故事。arXiv:1212.4414v1

Bohm, D. 狹義相對論（W. A. Benjamin，1965）。

D’Inverno, R. 邁入愛因斯坦的相對論（牛津大學出版社，1992）。

Eagle, A. 關於 Dolby 和 Gull 關於雷達時間和雙胞胎“悖論”的註記。美國物理學雜誌。2005 年，第 73 卷；第 10 期，第 976-978 頁。http://arxiv.org/PS_cache/physics/pdf/0411/0411008v2.pdf

Langevin, P. (1911) 空間和時間的演變 Scientia 10 (1911), 31-34

長度收縮的本質

根據狹義相對論，像測量桿這樣的物體由分佈在空間和時間中的事件組成，而一個三維杆是構成杆在單個時刻的事件。然而，從同時性的相對性可以明顯看出，兩個相對運動的觀察者將擁有不同的事件集，這些事件集在給定的時刻存在。這意味著，兩個相對於彼此運動的觀察者通常會觀察到由**不同**的事件集組成的測量桿。如果“杆”這個詞指的是被稱為杆的三維形式，那麼這兩個相對運動的觀察者將**觀察到不同的杆**。

可以使用閔可夫斯基圖來檢視測量桿在觀察者之間不同的方式。閔可夫斯基圖中對應於構成物體在一段時間內的所有事件的區域被稱為該物體的**世界線**。從下面的影像可以看出，長度收縮是由於各個觀察者在他們的現在時刻擁有物體世界線不同的部分的結果。

（應該記住，時空圖上的最長長度通常在現實中是最短的）。

有時人們說，長度收縮發生是因為物體旋轉到時間軸上。這實際上是一個半真半假的答案，三維杆實際上並沒有旋轉，而是觀察到的四維杆的三維切片發生了變化，使得它看起來像是杆旋轉到時間軸上。在狹義相對論中，不是杆旋轉到時間軸上，而是觀察者對杆世界線的切片旋轉。

毫無疑問，杆世界線的切片對於相對運動的觀察者來說確實有不同的長度。組成杆世界線的事件是否總是存在，這是一個哲學思辨的問題。

進一步閱讀

Vesselin Petkov. (2005) 存在一種替代塊宇宙觀的方案嗎？

Dragan V Redžić (2010). 相對論長度之苦的延續

杆倉悖論

相對論中的長度收縮是對稱的。當兩個相對運動的觀察者彼此經過時，他們都測量到長度的收縮。

（注意，閔可夫斯基度量涉及時間的位移的減法，因此，在二維紙張上看起來最長的長度在 (3+1)D 現實中往往是最短的長度）。

長度收縮的對稱性導致了兩個問題。首先，一系列事件如何被另一個觀察者觀察到是同時發生的事件？這個問題導致了德布羅意波和量子理論的概念。其次，如果一個杆在一個參考系中同時位於兩個點之間，那麼它如何在另一個參考系中被觀察到依次位於這兩個點之間？例如，如果一個杆以高速進入一棟建築，一個觀察者如何發現它完全在建築物內，而另一個觀察者發現杆的兩端在不同的時間分別與建築物兩端相對？如果杆撞到建築物的末端會發生什麼？第二個問題被稱為“杆倉悖論”或“梯子悖論”。

杆倉悖論陳述如下：假設一個以 0.75c 的速度奔跑並攜帶一根 15 米長的水平杆走向一個長 10 米的穀倉，穀倉有前後兩個門。當跑步者和杆進入穀倉時，地面觀察者關閉然後開啟兩扇門（透過遙控），使跑步者和杆暫時被困在穀倉內，然後從後門走出穀倉。

人們可能會驚訝地看到一根 15 米長的杆能裝進一個 10 米長的穀倉。但是，杆相對於地面觀察者處於運動狀態，地面觀察者測得杆的長度收縮到 9.9 米（使用方程檢查）。

當我們考慮跑步者的觀點時，“悖論”就出現了。跑步者看到穀倉收縮到 6.6 米。因為杆處於跑步者的靜止參考系中，所以跑步者測量到它的長度是 15 米。現在，我們如何才能讓我們的超級英雄安全地穿過穀倉？

“悖論”的解決在於同時性的相對性。地面觀察者測量到兩扇門的關閉是同時發生的。然而，由於兩個門位於不同的位置，所以跑步者說它們不是同時關閉的。後門先關閉然後開啟，讓杆的前端離開。穀倉的前門直到杆的後端經過時才關閉。

如果後門保持關閉並由某種不可穿透的材料製成會發生什麼？我們能否透過在杆完全在穀倉內時關閉前門來將杆困在穀倉內，這是根據地面觀察者的說法？當杆的前端撞到後門時，關於這種撞擊的資訊將以衝擊波的形式沿杆向後傳播。資訊不能以超過 c 的速度傳播，因此杆的後端將繼續以其原始速度向前運動，直到波到達它。即使衝擊波以光速傳播，它也不會在杆的後端經過前門之後到達杆的後端，即使在跑步者的參考系中也是如此。因此，當前門關閉時，整個杆（雖然非常壓縮）將在穀倉內。如果它是無限彈性的，它最終會被壓縮並“彈簧載入”到封閉穀倉的內部。

長度收縮的證據，無限直電流的場

長度收縮可以在無限長直電流的場中直接觀察到。下圖展示了這種情況。

非相對論電磁學使用以下公式描述由於電荷產生的電場

$E={\frac {\lambda }{2\pi \epsilon _{0}r}}$

並使用畢奧-薩伐爾定律描述由無限長直電流產生的磁場

$B={\frac {\mu _{0}I}{2\pi r}}$

或者使用電荷密度（從 $I=\lambda v$ 其中 $\lambda$ 是單位長度上的電荷量)

$B={\frac {\mu _{0}\lambda v}{2\pi r}}$

利用相對論，可以證明上述磁場公式可以透過對電場的長度收縮的相對論效應來推匯出來，因此我們所說的“磁場”可以理解為對單一現象的相對論觀察結果。相對論計算如下。

如果 Jim 相對於導線以與負電荷相同的速度運動，他會看到導線相對於 Bill 發生收縮。

$l_{+}=l{\sqrt {1-v^{2}/c^{2}}}$

Bill 應該看到沿導線運動的電荷之間的空間也收縮了相同的量，但電中性的要求意味著運動的電荷將被分散以匹配導線中固定電荷的參考系。

這意味著 Jim 看到負電荷被分散，使得

$l_{-}={\frac {l}{\sqrt {1-v^{2}/c^{2}}}}$

Jim 觀察到的淨電荷密度為

$\lambda ={\frac {q}{l_{-}}}-{\frac {q}{l_{+}}}$

代入

$\lambda ={\frac {q}{l}}({\sqrt {1-v^{2}/c^{2}}}-{\frac {1}{\sqrt {1-v^{2}/c^{2}}}})$

使用二項式展開

$\lambda ={\frac {q}{l}}(1-{\frac {v^{2}}{2c^{2}}}-1-{\frac {v^{2}}{2c^{2}}})$

因此，考慮到淨正電荷，正電荷是固定的

$\lambda ={\frac {qv^{2}}{lc^{2}}}$

Jim 位置處的電場由下式給出

$E={\frac {\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

吉姆所在位置的電場力由 $F=Eq$ 給出，即

$F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

現在，根據經典電磁學

$c^{2}={\frac {1}{\epsilon _{0}\mu _{0}}}$

所以將此代入 $F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

(1) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

這是比爾觀察到的相對論電場力的公式，它表現為磁力。這與非相對論磁力計算結果如何比較？根據經典公式，吉姆位置上的電荷受到的磁場力為

$F=Bqv$

根據畢奧-薩伐爾定律，該力為

(2) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

這表明吉姆所經歷的相對論電場力的公式與經典磁力公式相同。

可以看出，一旦理解了時空的概念，這兩個場的統一就變得簡單明瞭。吉姆相對於導線以與負電荷載流子相同的速度運動，所以吉姆只感受到電場。比爾相對於導線是靜止的，他觀察到導線中的電荷是平衡的，而吉姆觀察到電荷不平衡。比爾將吉姆與載流子之間的吸引歸因於“磁場”。

重要的是要注意，與上面給出的長度收縮解釋一樣，構成吉姆負電荷流的事件與構成比爾負電荷流的事件不同。比爾和吉姆的負電荷佔據了時間上的不同時刻。

順便說一句，導線中電子的漂移速度約為每秒一毫米，但導線中存在大量的電荷（參見下面的連結）。

進一步閱讀

Purcell, E. M. 電和磁。伯克利物理課程。第 2 卷。第 2 版。紐約，紐約：麥格勞-希爾。1984 年。ISBN: 0070049084。

有用連結

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmmic.html

http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/releng.html

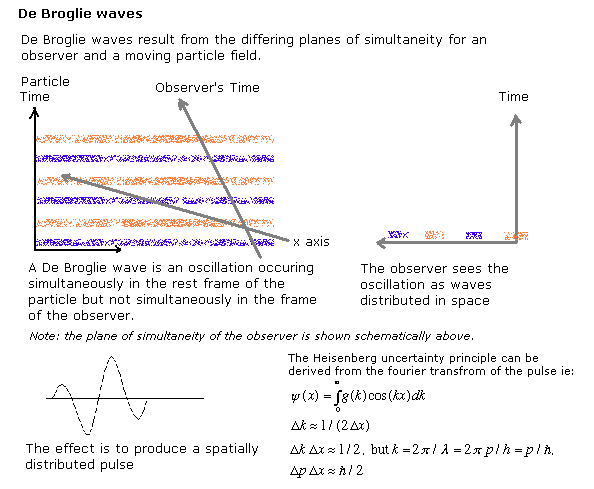
德布羅意波

德布羅意注意到，宇宙的不同三維部分會導致觀察者的靜止系中的振盪在運動的觀察者的靜止系中表現為波列。

他將這一洞察與愛因斯坦關於能量量子化的思想結合起來，為量子理論奠定了基礎。德布羅意的洞察力也是對上面給出的長度收縮描述的間接證明——相對運動的觀察者擁有四維宇宙中不同的三維切片。物質波的存在是同時性相對性的直接實驗證據。

進一步閱讀：de Broglie, L. (1925) 關於量子理論。RECHERCHES SUR LA THEORIE DES QUANTA（Ann. de Phys., 10e s´erie, t. III (Janvier-F ´evrier 1925)）的翻譯。作者：A. F. Kracklauer。 http://replay.web.archive.org/20090509012910/http://www.ensmp.fr/aflb/LDB-oeuvres/De_Broglie_Kracklauer.pdf

貝爾飛船悖論

貝爾設計了一個思想實驗，稱為“宇宙飛船悖論”，以探究長度收縮是否涉及力以及這種收縮是否是空間的收縮。在宇宙飛船悖論中，兩艘宇宙飛船由一根細而硬的繩子連線，並且都以相等的線性加速度加速到速度 $v$ 相對於地面，在該速度下，在狹義相對論版本的悖論中，加速度停止。兩艘宇宙飛船的加速度被安排成根據地面觀察者相等，因此，根據地面觀察者，宇宙飛船將保持相同的距離。問題是繩子是否會斷裂。

考慮這個問題時，研究一艘宇宙飛船會發生什麼是有幫助的。如果一艘具有尾部推進器的宇宙飛船根據地面觀察者線性加速到速度 $v$ ，那麼地面觀察者將觀察到它在運動方向上收縮。在收縮期間，宇宙飛船前部的加速度將略小於宇宙飛船後部的加速度，然後在尾部加速度和增加的收縮停止後，突然達到一個高值，使前部和後部的速度相等。從地面觀察，可以觀察到，總的來說，尾部的加速度可以是線性的，但前部的加速度是非線性的。

在貝爾的思想實驗中，兩艘宇宙飛船都被人工限制為根據地面觀察者具有恆定加速度，直到加速度停止。不允許突然調整。此外，不允許在元件的前部和後部之間的加速度之間存在差異，因此任何收縮趨勢都需要作為繩子的張力和伸長來承受。

這個悖論最有趣的部分是宇宙飛船之間的空間發生了什麼。從地面觀察，宇宙飛船將保持相同的距離（實驗被安排來實現這一點），而根據宇宙飛船上的觀察者，它們似乎會越來越分開。這意味著加速度在不同的參考系之間不是不變的（見第二部分），並且作用於宇宙飛船的力實際上會受到每個參考系觀察到的宇宙飛船分離差異的影響。

上面關於長度收縮本質的部分表明，當繩子的速度發生變化時，地面上的觀察者會觀察到構成繩子的事件集合發生變化。這些新事件定義了一條比原來更短的繩子。這意味著，從地面觀察，繩子確實會試圖收縮，並且從宇宙飛船觀察，它會在張力下被拉伸。如果繩子無法承受運動參考系中的伸長和張力或靜止參考系中的張力，它就會斷裂。

貝爾宇宙飛船悖論的另一個有趣方面是，在宇宙飛船的慣性系中，由於同時性的相對性，前導宇宙飛船將始終比後導宇宙飛船運動得略快，因此宇宙飛船-繩索系統在兩艘宇宙飛船的參考系中加速度停止之前，不會形成一個真正的慣性參考系。加速度停止的非同步性表明，在任何一艘宇宙飛船的參考系中，前導宇宙飛船都比後導宇宙飛船先達到最終速度。然而，這種時間差非常小（小於影響以光速 $x/c>vx/c^{2}$ 在繩索上傳播的時間）。

在這個階段，有必要警告不要將狹義相對論外推到廣義相對論 (GR) 的領域。SR 無法自信地應用於加速系統，這就是為什麼上面的評論僅限於定性觀察。

進一步閱讀

貝爾，J. S. (1976)。量子力學中的可言與不可言。劍橋大學出版社 1987 ISBN 0-521-52338-9

Hsu，J-P 和 Suzuki，N. (2005) 加速參考系的擴充套件洛倫茲變換和“兩宇宙飛船悖論”的解 AAPPS 公告 2005 年 10 月 p.17 http://www.aapps.org/archive/bulletin/vol15/15-5/15_5_p17p21%7F.pdf

Matsuda，T 和 Kinoshita，A (2004。狹義相對論中的兩艘宇宙飛船的悖論。AAPPS 公告 2004 年 2 月 p3。 http://www.aapps.org/archive/bulletin/vol14/14_1/14_1_p03p07.pdf

橫向多普勒效應

時間膨脹的存在意味著從朝向或遠離觀察者運動的光源發射的光的頻率在垂直於運動方向的方向上應該發生紅移。橫向多普勒效應由下式給出

\nu =\nu ^{\prime }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}

其中 $\nu$ 是觀察到的頻率，而 $\nu ^{\prime }$ 是如果光源相對於觀察者靜止時的頻率（**固有頻率**）。

這種效應最早由艾夫斯和斯蒂爾韋爾在 1938 年證實。橫向多普勒效應是純粹的相對論效應，已被用作時間膨脹發生的證明示例。

角度的相對論變換

如果一根杆子與其朝向或遠離觀察者的運動方向成一定角度，則其在運動方向上的長度分量將收縮。這意味著觀察到的角度在參考系變化期間也會發生變換。假設運動發生在 x 軸上，假設杆子在靜止系中的固有長度（靜止長度）為 $L^{\prime }$ 米，並且與 x' 軸成 $\theta ^{\prime }$ 度角。與軸形成的角度的正切為

杆靜止參考系中的正切 =

\tan \theta ^{\prime }={\frac {L_{y}^{\prime }}{L_{x}^{\prime }}}

觀察者參考系中的正切 =

\tan \theta ={\frac {L_{y}}{L_{x}}}

因此

{\frac {\tan \theta }{\tan \theta ^{\prime }}}={\frac {L_{y}L_{x}^{\prime }}{L_{y}^{\prime }L_{x}}}

但是

L_{x}=L_{x}^{\prime }{\sqrt {1-v^{2}/c^{2}}}

並且

L_{y}=L_{y}^{\prime }

所以

\tan \theta ={\frac {\tan \theta ^{\prime }}{\sqrt {1-v^{2}/c^{2}}}}

表明，觀察者觀察到的與運動方向成角的角度會隨著速度增加。

運動物體與 x 軸所成的角度也涉及速度的變換，以計算正確的入射角。

速度相加

兩個以 v 米/秒的速度彼此相對運動的觀察者如何比較他們對第三個物體的速度的觀察結果？

假設其中一個觀察者測得物體的速度為 $u^{'}$ ，其中

$u^{'}={\frac {x^{'}}{t^{'}}}$

座標 $x^{'}$ 和 $t^{'}$ 由洛倫茲變換給出

$x^{'}={\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}$

和

$t^{'}={\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

但是

$x^{'}=u^{'}t^{'}$

所以

${\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}=u^{'}{\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

因此

$x-vt=u^{'}(t-vx/c^{2})$

注意相位項 $vx/c^{2}$ 的作用。該方程可以改寫為

$x={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}t$

鑑於 $x=ut$

$u={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}$

這就是著名的 **相對論速度加法定理**，它適用於平行於相互運動方向的速度。

時間膨脹的存在意味著，即使物體垂直於運動方向運動，相對運動的觀察者對物體的速度報告也會出現差異。如果在 x 方向上存在任何速度分量 ( ${u_{x}}$ ， ${{u^{'}}_{x}}$ )，那麼相位會影響時間測量，進而影響垂直於 x 軸的速度。下表總結了空間各個方向上的相對論速度加法。

${u^{'}}_{x}={\frac {(u_{x}-v)}{(1-u_{x}v/c^{2})}}$	$u_{x}={\frac {({u^{'}}_{x}+v)}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{y}={\frac {u_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{y}={\frac {{u^{'}}_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{z}={\frac {u_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{z}={\frac {{u^{'}}_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}</P>$