狹義相對論/波

狹義相對論

狹義相對論的應用

在本章中，我們將繼續研究狹義相對論，將前一章中開發的思想應用於波的研究。

首先，我們將展示如何在時空的背景下描述波。然後我們看到，沒有優先參考系（例如支援它們的介質）的波，受狹義相對論的約束，具有特定形式的色散關係。這種色散關係結果是量子力學中相對論物質波的色散關係。

其次，我們將研究多普勒頻移現象，其中波的頻率在不同的座標系中取不同的值。

第三，我們將展示如何在相對論上一致地新增速度。這在討論狹義相對論中的粒子行為時也會很有用。

一個新的數學概念將在相對論波的背景下呈現，即時空向量或四向量。用相對論標量和四向量完全寫出物理定律確保它們在所有慣性參考系中都有效。

時空中的波

我們現在看看時空中的波的特徵。回想一下，一個空間維度的波可以用

$A(x,t)=A_{0}\sin(kx-\omega t)\,$

其中 $A_{0}$ 是波的（常數）振幅， $k$ 是波數， $\omega$ 是角頻率，並且量 $\phi =kx-\omega t$ 被稱為波的相位。對於三維空間中的波，波以類似的方式表示，

$A(\mathbf {x} ,t)=A_{0}\sin(\mathbf {k} \cdot \mathbf {x} -\omega t)$

其中 $\mathbf {x}$ 現在是位置向量， $\mathbf {k}$ 是波向量。波向量的幅度， $|\mathbf {k} |=k$ 只是波的波數，該向量的方向表示波移動的方向。在這種情況下，波的相位是 $\phi =\mathbf {k} \cdot \mathbf {x} -\omega t$ .

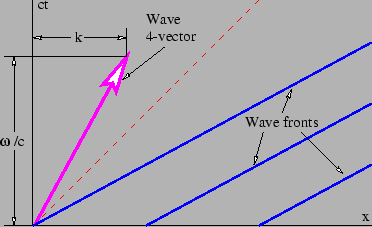Figure 5.1: Sketch of wave fronts for a wave in spacetime.

圖 5.1：時空波前示意圖。大箭頭是相關的波四向量，其斜率為

\omega /ck

。波前的斜率是它的倒數，

ck/\omega

.

在一維情況下 $\phi =kx-\omega t$ 。波前具有恆定相位 $\phi$ ，因此求解這個方程關於 $t$ 並乘以真空中的光速 $c$ ，我們可以得到波前世界線的方程

$ct={\frac {ckx}{\omega }}-{\frac {c\phi }{\omega }}={\frac {cx}{u_{p}}}-{\frac {c\phi }{\omega }}\quad {\mbox{(wave front).}}$

世界線在時空圖中的斜率是 $x$ 的係數，或 $c/u_{p}$ ，其中 $u_{p}=\omega /k$ 是相速度。

相對論在波中的應用

回到波的相位，我們立即看到

\phi =\mathbf {k} \cdot \mathbf {x} -\omega t=\mathbf {k} \cdot \mathbf {x} -(\omega /c)(ct)={\underline {k}}\cdot {\underline {x}}.

因此，寫波的一種簡潔方式是 $A({\underline {x}})=\sin({\underline {k}}\cdot {\underline {x}}).$ (6.8)

由於 ${\underline {x}}$ 已知是四向量，並且波的相位已知是與參考系無關的標量，因此可以得出 ${\underline {k}}$ 實際上是一個四向量，而不僅僅是一組數字。因此，波四向量的長度的平方也必須是與參考系無關的標量

{\underline {k}}\cdot {\underline {k}}=\mathbf {k} \cdot \mathbf {k} -\omega ^{2}/c^{2}=const.

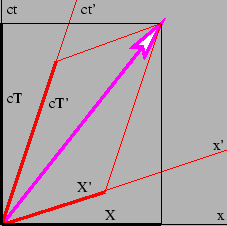
Figure 5.2: Resolution of a four-vector into components in two different reference frames.

四向量在兩個不同參考系中的分量分解。

讓我們精確地回顧一下這意味著什麼。如圖所示，我們可以將位置四向量x分解成兩個不同參考系中的分量，例如(X,T)和(X′,T′)，但這只是寫同一個向量的不同方式。

這與三維向量在旋轉系中具有不同的分量完全相同。

類似地，就像三維向量在所有系中具有相同的幅度一樣，四向量也是如此；即，

X^{2}-c^{2}T^{2}=X^{\prime 2}-c^{2}T^{\prime 2}

將此應用於波動四向量，我們可以推斷出

k^{2}-c^{-2}\omega ^{2}=k^{\prime 2}-c^{-2}\omega ^{\prime 2}

其中，k 和 ω 的無撇號值和有撇號值分別指波動四向量在兩個不同參考系中的分量。

到目前為止，這個論點適用於任何波。然而，波可以分為兩類，一類是存在一個特殊參考系的波，另一類是不存在這種特殊參考系的波。

例如，聲波在氣體靜止的參考系中看起來最簡單。光在折射率不等於1的材料介質中傳播也是如此。在這兩種情況下，只有在材料介質靜止的參考系中，波的速度在各個方向上才相同。

如果沒有材料介質，就沒有明確的方法來找到一個特殊的參考系，因此這些波必須屬於第二類。這包括真空中所有波，例如光。

在這種情況下，可以進行以下論證。一個相對於頻率為 ω 和波數為 k 的波運動的觀察者，看到頻率為 ω′ 和波數為 k′ 的波。如果觀察者能以任何方式判斷這些波來自一個相對於它們運動的源，那麼他們就可以利用這一點來識別這些波的特殊參考系，因此這些波看起來就像來自一個頻率為 ω 的靜止源一樣。

這迫使我們得出結論，對於這種波

\omega ^{2}=c^{2}k^{2}+\mu ^{2}\,

其中 μ 是一個常數。真空中所有的波都必須具有這種形式，這比經典物理學中更受限制的選擇。

在經典物理學中，光的 ω 和 k 之間的關係為

\omega =ck\,

在相對論物理學中，我們已經看到，對於沒有特殊參考系的波（如光），ω 和 k 之間的關係為

\omega ^{2}=c^{2}k^{2}+\mu ^{2}\,

如果 μ=0，則相對論方程簡化為經典方程，因此我們可以假設，對於光，μ 確實等於零。

這意味著光沒有最低頻率。

如果 μ 不為零，則所描述的波是色散波。相速度為

u_{p}={\frac {\omega }{k}}={\sqrt {c^{2}+{\frac {\mu ^{2}}{k^{2}}}}}

這個相速度總是大於 c，這乍看起來似乎是一個非物理的結論。然而，波的群速度為

u_{g}={\frac {d\omega }{dk}}={\frac {kc^{2}}{\sqrt {k^{2}c^{2}+\mu ^{2}}}}={\frac {kc^{2}}{\omega }}={\frac {c^{2}}{u_{p}}}

它總是小於 c。由於波包以及訊號以群速度傳播，因此即使相速度超過光速，這種型別的波在物理上也是合理的。

這種波的另一個有趣的性質是波動四向量平行於時空中的波包世界線。以下論證很容易證明這一點。

波動四向量的空間分量為 k，時間分量為 ω/c。因此，四向量在時空圖上的斜率為 ω/kc。然而，以群速度移動的波包世界線的斜率為 c/u_g，這也等於 ω/kc。

注意，當 k 為零時，我們有 ω=μ。在這種情況下，波的群速度為零。因此，我們有時將 μ 稱為波的靜止頻率。

多普勒效應

你可能聽說過火車鳴笛的聲音如何隨著火車經過你而發生變化。當火車駛近時，音調或頻率比火車駛離時高。這被稱為多普勒效應。如果你經過一個聲源，也會發生類似但不同的效應。如果一個靜止的汽笛在鳴叫，從一輛移動的汽車上聽到的音調在朝聲源移動時比離開時高。因此，第一個案例是運動的聲源，而第二個案例是運動的觀察者。

在本節中，我們將計算多普勒效應，因為它適用於光在真空中傳播。下圖顯示了計算光波前之間時間的幾何形狀，用於靜止和移動參考系。