假設你有一個放在地上的箱子,並且這個箱子正被兩個方向的特定力拉動。你可以透過找到作用在箱子上的合力來預測箱子的運動。如果每個力向量(其中大小是繩索的張力,方向是繩索“指向”的方向)都可以測量,則可以將這些向量相加以得到合力。有兩種方法可以進行向量加法
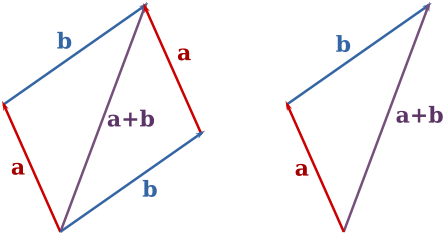 兩個向量的加法
兩個向量的加法
這是一種圖形化的方法來進行向量加法。首先,一些術語
- 向量的尾部是它起源的地方。
- 向量的頭部是它指向的地方。頭部是帶有箭頭的那一端。
這種方法最容易使用繪圖紙執行。建立一個直角座標系,並按比例繪製第一個向量,其尾部位於原點。然後,繪製第二個向量(同樣,按比例繪製),使其尾部與第一個向量的頭部重合。然後,和向量的屬性如下
- 和向量的長度是從原點到第二個向量頭部的距離。
- 和向量的方向是角度。
在右側的影像中,向量 (10, 53°07'48") 和 (10, 36°52'12") 正在以圖形方式相加。結果是 (19.80, 45°00'00")。(我如何如此精確地測量出這些角度?我故意這麼做的。)
平行四邊形法則的原生向量格式是“極座標形式”。
當使用計算方法時,必須將每個向量分解成其x和y分量。然後,只需將相應的分量相加。
如果一個向量由 (r, θ) 給出,其中r是長度,θ是方向,
如果一個向量由 給出,
給出,


請記住,arctan() 函式僅返回 [-π/2, π/2] 範圍內的值;因此,如果你的向量在第二或第三象限,則必須將π新增到從 arctan() 函式返回的任何角度。
再次參考右側的影像,請注意第一個向量可以表示為 ,第二個等效於
,第二個等效於 。(驗證一下。)然後,只需將分量相加
。(驗證一下。)然後,只需將分量相加

你應該驗證 等於 (19.80, 45°00'00")。
等於 (19.80, 45°00'00")。
有兩種方法可以進行向量乘法。我不會在這裡深入探討具體的應用;在閱讀本書的過程中,你會看到很多這樣的應用。
兩個向量的點積的結果是一個標量。點積是分量乘積的和。例如
< 1 , 2 >
∙ < 3 , 4 >
-----------
| +-----> 2 x 4 = 8
+---------> 1 x 3 = 3
------
11
 使用點積計算甲烷等對稱四面體分子的鍵角
使用點積計算甲烷等對稱四面體分子的鍵角
向量、它們的長度以及它們之間角度之間的一個有用關係由點積的定義給出

- 向量
 和
和  。
。
- 向量的大小分別為
 和
和  。
。
- 這兩個向量之間的夾角為
 。
。
兩個向量的叉積得到另一個向量。叉積僅適用於三維空間向量。請記住三個單位向量
 是沿著 *x* 軸的單位向量
是沿著 *x* 軸的單位向量 是沿著 *y* 軸的單位向量
是沿著 *y* 軸的單位向量 是沿著 *z* 軸的單位向量
是沿著 *z* 軸的單位向量
現在,如果您有兩個向量 和
和  ,叉積可以透過求解以下行列式得到
,叉積可以透過求解以下行列式得到

有關如何求解行列式的更多資訊,請參閱下面的外部連結。
兩個向量的叉積、這兩個向量的長度以及這兩個向量之間的夾角由以下關係給出

從幾何上講,叉積得到一個垂直於這兩個引數的向量。請注意對“一個”向量的引用,而不是“該”向量。這是因為有無限多個向量垂直於兩個非零向量。叉積的方向可以使用 *右手定則* 來確定:伸出你的右手手指,將你的伸直的手放在第一個向量上,將你的指尖指向與向量相同的方向。將你的手指從第一個向量到第二個向量穿過短角捲曲。你的拇指將指向乘積向量方向。
- 單位向量與自身點積得到 *1*。
- 單位向量與另一個不同的單位向量點積得到 *0*。
按照此順序排列單位向量: 。從第一個向量開始,移動到第二個向量,然後繼續到叉積。如果您首先立即向右移動,則答案為正。如果您首先向左移動,則答案為負。例如
。從第一個向量開始,移動到第二個向量,然後繼續到叉積。如果您首先立即向右移動,則答案為正。如果您首先向左移動,則答案為負。例如


給定向量 和標量 r
和標量 r





維基百科上的行列式































