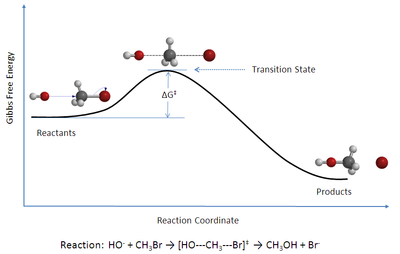
 圖 1:溴甲烷與氫氧根陰離子雙分子親核取代 (SN2) 反應的反應座標圖
圖 1:溴甲烷與氫氧根陰離子雙分子親核取代 (SN2) 反應的反應座標圖
化學動力學描述了物種濃度透過化學反應隨時間的變化速率。
- 速率=
![{\displaystyle k[A]^{v_{a}}[B]^{v_{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04444b893cbcb8218edf488f91e98ab204278f02)
速率常數 k 取決於反應的化學物質和反應條件(即溫度)。
使用速率理論,可以透過統計熱力學估計基本氣相化學反應的速率常數。艾林傳統過渡態理論是最簡單和使用最廣泛的理論之一。
在艾林傳統過渡態理論中,化學反應的速率常數可以用過渡態和反應物的配分函式來表示。 是反應的勢壘高度。
是反應的勢壘高度。

過渡態理論在其推導中依賴於三個關鍵假設。
- 反應物與過渡態結構處於不斷的平衡狀態。
- 粒子的能量服從玻爾茲曼分佈。
- 一旦反應物變成過渡態,過渡態結構就不會塌回反應物。
假設一個反應,其中反應物 A 和 B 轉換成過渡態 C
![{\displaystyle {\ce {A+B<=>{}[C]^{\ddagger }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aae1d9631c9c68b5f13f1e359d1bf9475014d1d)
平衡常數 K‡ 可以用反應物和過渡態的濃度來表示。
![{\displaystyle K^{\ddagger }={\frac {\ce {[C]^{\ddagger }}}{\ce {[A][B]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb54ef9dc837eff8cc17cec2f0c692d1bc13b4ae)
這個反應作為平衡存在,因為我們假設並非每次碰撞都會導致過渡態的形成。用配分函式重寫濃度,得到下面的方程。

艾林方程也可以用熱力學引數來表示。標準自由能 ΔG‡ 可以用平衡常數來表示。


利用標準吉布斯能量方程,艾林方程可以寫成

這裡, 是活化焓,代表過渡態結構的焓或能量穩定性;它是斷裂反應物鍵並形成過渡態所需的能量。類似於標準焓,負值代表更穩定的能量結構,反之亦然。
是活化焓,代表過渡態結構的焓或能量穩定性;它是斷裂反應物鍵並形成過渡態所需的能量。類似於標準焓,負值代表更穩定的能量結構,反之亦然。  是活化熵,代表過渡態的熵或無序程度,是過渡態與反應物相比的可達狀態數。同樣,正熵代表更無序的系統,而負熵對應於更有序的系統。
是活化熵,代表過渡態的熵或無序程度,是過渡態與反應物相比的可達狀態數。同樣,正熵代表更無序的系統,而負熵對應於更有序的系統。
使用艾林方程的熱力學表示可以預測反應可能採取的機理型別。締合機理涉及一個分子與另一個分子鍵合形成過渡態,而解離機理涉及一個分子斷裂形成過渡態。一般來說,當過渡態的熵低於反應物時,就會發生締合機理,因此過渡態更加有序;這意味著熵的變化為負。其結果是熵降低,結構更加有序,可達狀態更少。相反,當過渡態的熵為正,或相對於反應物而言過渡態的熵更高時,就會發生解離機理。因此,過渡態比初始反應物更無序。
TST 需要計算過渡態結構的配分函式。

過渡態的平動和轉動配分函式與反應物物種中使用的形式相同。振動配分函式略有不同,因為對應于越過勢壘的振動從該項中去除(它“變成” 項。因此,振動配分函式中少了一個項。對於非線性過渡態,將有
項。因此,振動配分函式中少了一個項。對於非線性過渡態,將有 項。對於線性過渡態,將有
項。對於線性過渡態,將有 項。
項。

使用該理論計算速率常數需要知道過渡態的所有結構和機械性質。這是一個挑戰,因為很難使用光譜法測定過渡態的結構性質,而過渡態通常只存在 10-200 fs。相反,計算化學通常用於計算過渡態的性質。
計算 H + H2 在 300 K 時的速率常數。
H + H2 → H2 + H
為了計算速率常數,需要以下內容,對於反應物和過渡態
- 同位素的質量
- 振動頻率 (qvib)
- 慣性矩 (qrot)
- 電子簡併度
- 反應勢壘高度
| 物種 |
振動 |
 (cm-1) (cm-1) |
| H2 |
H-H 伸縮 |
4401.1272
|
| H-H-H‡ |
H-H-H 彎曲(簡併度為 2) |
875.62
|
| H-H-H‡ |
H-H-H 對稱伸縮 |
2050.67
|
反應物的 R = 0.743 Å,過渡態的 R = 0.931 Å  ‡ = 38.61 kJ mol-1
‡ = 38.61 kJ mol-1
平動配分函式

對於 H2: 

對於 H-H-H:

旋轉配分函式
對於 H2 : 


對於 H-H-H: 


振動配分函式
對於 H2:



速率常數 k




w:過渡態理論
Atkins, P., de Paula, J., 物理化學基礎, 第 5 版;牛津大學出版社,2009 年。


![{\displaystyle k[A]^{v_{a}}[B]^{v_{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04444b893cbcb8218edf488f91e98ab204278f02)


![{\displaystyle {\ce {A+B<=>{}[C]^{\ddagger }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aae1d9631c9c68b5f13f1e359d1bf9475014d1d)
![{\displaystyle K^{\ddagger }={\frac {\ce {[C]^{\ddagger }}}{\ce {[A][B]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb54ef9dc837eff8cc17cec2f0c692d1bc13b4ae)






























