結核病統計/分析

關於結核病的一些事實

結核病 (TB) 是一種常見的致命性傳染病，如今正在捲土重來。據世界衛生組織估計，目前全球超過三分之一的人口體內攜帶這種細菌。艾滋病毒陽性的人感染結核分枝桿菌的風險要高得多，因為他們的免疫系統受到艾滋病毒的損害。其他可能導致結核病流行的指標包括營養不良、衛生條件差以及缺乏醫療措施。

摘要

結核病長期被忽視，在世界許多地區已達到流行病的程度。這種傳播的原因可能是什麼？如上所述，人們似乎對大多數促成這種疾病的因素達成了共識。然而，關於結核病流行與某些因素之間關係的新假設必須透過統計方法進行量化，這些方法是用統計軟體進行的。

因此，根據孔子的一句名言，我們的分析目標是道，更準確地說，是評估和處理多元資料集的方法。然而，在分析過程中，我們將提出一些關於變數關係的假設。快速瀏覽一下多元分析及其小節。

用於此次分析的程式是MDTech XploRe 軟體。分析的所有主要步驟都可以透過本研究中提供的程式程式碼輕鬆地重現（通常與影像空間中的圖形一起）。您只需要原始資料，名為"datest.csv"，可在http://www.quantlet.org/mdbase/上獲得，以及XploRe 軟體的免費學術版。

原始資料集描述

該分析基於名為"datest.csv"的資料集，該資料集可在MD*Base的主頁上獲得。

原始資料集 (datorg.csv) 中出現的缺失值已使用不同的方法替換為估計值，例如相鄰國家平均值、線性迴歸和其他技術。由於資料是從聯合國收集的，您可以在聯合國統計司的主頁上仔細檢視每個變數的定義。

該資料集包含 163 個觀測值和 16 個變數。第一個變數是文字變數，顯示每個國家的名稱，第二個變數將每個國家分配到一個大陸，因此是名義變數（從 1 到 6）。所有其他變數在以下表格中描述

表 1 - 變數

編號	標題	型別	備註
1.	國家	文字	每個國家的名稱
2.	大陸	名義	1：亞洲，2：北美洲，3：南美洲，4：非洲，5：歐洲，6：澳大利亞和洋洲
3.	人口	公制	每個國家的人口總數
4.	安全套使用率	公制	女性使用安全套與其他避孕措施的比例（以百分比表示）
5.	艾滋病估計死亡人數	公制	與艾滋病相關的死亡總數（估計）
6.	瘧疾	公制	流行總人數
7.	結核病	公制	每 100,000 人的患病率
8.	藥品	公制	獲得基本藥物（如世界衛生組織所列）的比例（以百分比表示）
9.	教育	公制	相關年齡組的入學率，分為四個組 < 50 %，50 – 80 %，80 – 95 %，> 95 %
10.	識字率	公制	以百分比表示的比率
11.	衛生設施	公制	獲得基本衛生設施的比例（以百分比表示）
12.	水	公制	獲得改良飲用水的比例（以百分比表示）
13.	二氧化碳	公制	每人噸
14.	網際網路	公制	網際網路接入總數
15.	個人電腦使用者	公制	總數
16.	電話	公制	總數

資料轉換

從表 1 可以看出，變數是以不同的尺度測量的。結核病的測量單位是每 100,000 人，而例如估計的與艾滋病相關的死亡人數則以人口總數表示。因此，我們分析的第一步是重新排列資料集，使其更有序，並以更合適的方式進行縮放。

以下程式用於

• 在資料集中新增一列包含國家程式碼
• 將所有三種疾病的比例標準化為“每 100,000 人”
• 將網際網路接入總數、個人電腦總數和電話線總數更改為相對數量
• 重新排列變數順序，使
  • 前三列包含國家程式碼、大陸程式碼和人口
  • 第四到第六列分別包含估計的艾滋病死亡人數、瘧疾患病率和結核病患病率的標準化值
  • 變數“安全套使用”出現在第八列，之後是其他變數，按原始順序排列

該程式將載入原始資料並建立兩個 CSV 檔案，分別包含重新排列的資料集（包括國家名稱）和僅包含國家名稱的檔案。在執行程式之前，請確保您已從MD*Base的主頁下載了原始資料"datest.csv"到已知的目錄中。

library("xplore")
library("stats")

; ----- Reading data ----------------------------------------------------------------------------

choose = "Read from:" | "Save as:" | "Save country info as:"

defaults1 = "C:\Dokumente und Einstellungen\All Users\Desktop\datest.csv"
defaults2 = "C:\Dokumente und Einstellungen\All Users\Desktop\UN_data_ordered.csv"
defaults3 = "C:\Dokumente und Einstellungen\All Users\Desktop\country.csv"

defaults = defaults1 | defaults2 | defaults3

v = readvalue(choose, defaults)

; ----- Transformation --------------------------------------------------------------------------

x=readcsvm(v[1])

num=1:163
data=num~x.double

country=x.text

pop=data[,3]

x=(data[,5|6]/pop)*100000
y=data[,14|15|16]/pop
data=data[,1:3]~x~data[,7|4|8:13]~y

l=list(country, data)

; ----- Saving ----------------------------------------------------------------------------------

writecsv(l,v[2])
writecsv(country,v[3])

單變數分析

首先，我們想概述一些關於解釋變數的描述性資料的概述，包括五數概括、偏度和峰度。偏度$s$和峰度$k$分別測量偏度和偏離正態分佈的程度

$s=\left[{\frac {1}{n}}\sum _{i=1}^{n}{\frac {(x_{i}-{\bar {x}})^{3}}{v^{3}}}\right]$;$k=\left[{\frac {1}{n}}\sum _{i=1}^{n}{\frac {(x_{i}-{\bar {x}})^{4}}{v^{4}}}\right]$

對於一個關於${\overline {x}}$對稱的分佈，偏度應該接近於 0。對於一個類似於正態分佈的分佈，峰度應該接近於 3。

表 2. 解釋變數的一些描述性資料

變數	最小值	25% 分位數	中位數	平均值	75% 分位數	最大值	偏度	峰度
安全套使用率	0	4.25	6.8	10.13	12.95	77.6	2.88	18.17
藥品	50	80	80	81.47	95	100	-0.78	2.42
教育	13.9	73.5	91.1	83.63	97.3	109.5	-1.33	4.22
識字率	24.5	83.4	95.6	88.34	99.3	100	-1.64	5.12
衛生設施	8	62	87	76.56	98	100	-0.96	2.71
水	24	71.5	87	81.06	98	100	-0.99	2.97
二氧化碳	0.02	0.41	1.97	4.67	6.26	90.74	6.52	61.37
網際網路	0	0	0.03	0.1	0.1	0.58	1.73	4.7
個人電腦使用者	0	0	0.03	0.1	0.11	0.60	2.02	6.23
電話	0	0.03	0.22	0.4	0.55	1.61	1.16	3.01

箱線圖、直方圖和分位數-分位數圖

現在，我們將透過傳統的單變數分析機制，觀察我們後期模型中所有感興趣的變數。為了得到一個綜合的概述，我們首先關注包含超過一個變數的資訊的多圖顯示。

圖 1，點選圖片檢視這些箱線圖的程式程式碼。

讓我們看看圖 1和圖 2，我們計算了資料中疾病的箱線圖和直方圖，包括結核病、瘧疾和艾滋病。

圖 2，點選圖片檢視這些直方圖的程式程式碼。

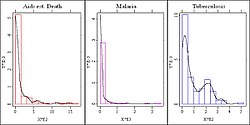
如上所述，所有三個變數都已轉換為每 100,000 人的比例。為了在圖 1中更好地視覺化，我們標準化了 x 軸，否則結核病和瘧疾的箱線圖將過於壓縮。對於所有三個變數，我們觀察到右偏斜，但異常值分佈的特徵差別很大。因此，對於結核病，我們只識別出一個異常值（柬埔寨），而對於艾滋病死亡，則顯示了 38 個異常值，其中 24 個是中等程度的（圓圈），14 個是更明顯的（十字）。我們決定識別這些異常值，結果表明大約 90% 的異常值是非洲國家，相應地，大約 72% 的非洲國家是異常值。是否應該在這裡排除整個大陸？絕對不應該，但這一事實為資料中可能存在的子組提供了一個提示。

圖 3，點選圖片檢視這些箱線圖的程式程式碼。

圖 4，點選圖片檢視這些直方圖的程式程式碼。

圖 3 到 5 為我們提供了對可能影響因變數結核病的解釋變數進行單變數分析的結果。

在圖 3中，我們看到了上面提到的箱線圖。請注意，我們以不同的比例顯示了箱線圖。前五個箱線圖以百分比衡量，而我們決定標準化較低箱線圖的 y 軸。關於獲取藥物箱線圖有一個重要的說明：雖然似乎只有一個異常值，但事實證明，這個“點”實際上是 37 個國家，它們都落在了 0% 到 50% 的類別中。

資料的偏度也可以被預料到，並在圖 4中得到證實，我們在其中顯示了平均偏移曲線和直方圖。再次引起我們注意的是，除獲取藥物外，上面的變數都向左偏斜，而下面的變數都向右偏斜。這意味著大多數國家的變數值在上面的部分比較高，而那些在下面的部分比較低。 圖 5顯示了分位數-分位數圖，用於比較每個變數與正態分佈。顯然，我們與 45 度線存在明顯的偏差，這表明這些變數不是正態分佈的。

總的來說，單變數分析的主要發現是，我們有非常偏斜的分佈，這些分佈在不同的變數之間部分重疊。這可能是單個維度之間強相關性的一個指標。無論如何，問題仍然存在，這些關係是線性的還是非線性的。此外，我們在資料集的不同維度中看到了很多異常值。因此，問題就出現了，一個維度中的異常值是否也是資料集中其他維度的異常值。這個問題將在下一節中討論。

使用簡單多元方法處理異常值

正如我們在單變數分析中所看到的，我們面臨著一個非常異質的資料集，具有極度偏斜的分佈，因此有很多觀察結果被顯示為異常值。這種情況甚至發展到幾乎要從分析中排除整個大陸，即非洲的艾滋病相關死亡率。這可能促使對非洲進行單獨的分析。

表 3 - 每個維度中的異常值數量

人口	艾滋病	瘧疾	結核病	避孕套使用	藥品	教育
20	24	37	1	9	31	7
識字率	衛生設施	水	二氧化碳	網際網路	個人電腦	電話
9	0	3	8	26	18	10

但是在這裡，我們的目標是找到更好地處理多維大型資料集的方法。因此，我們試圖找到一種方法來評估所有國家在其特定維度上的極端值。此外，我們希望獲得一個表，其中包含每個維度中“箱線圖異常值”的數量。因此，我們計算了一個 163 x 14 的矩陣，其中包含邏輯值 0 或 1，其中 1 表示觀察結果是異常值。使用此矩陣進行簡單的計算，會導致除了在表 3中顯示的每個維度中的異常值數量之外的其他結果。

圖 6，點選圖片檢視程式程式碼及其用途描述。

圖 6顯示了一個條形圖，其中國家根據單變數極端值或“箱線圖異常值”的數量進行分類。該圖表顯示，只有少數國家在四個維度上是箱線圖意義上的異常值，並且沒有一個國傢俱有超過四個極端值。“異常值程式”生成圖 6，並提供一個選項，可以決定觀察結果必須在多少個維度上成為單變數異常值才能被視為“多維異常值”。這些“多維異常值”然後用藍色標記，並與其他觀察結果一起顯示在星形圖中（或者，也可以選擇所謂的切爾諾夫-弗裡臉）。這有助於決定這些觀察結果是否真的與資料的其餘部分有很大不同。這個過程可以重複多次，直到找到一個令人滿意的異常值集，該集合將被排除在進一步分析之外（透過“異常值程式”提供儲存選項）。

然而，對於進一步的分析，我們決定不排除任何觀察結果，而是繼續使用整個資料集，因為即使每個觀察結果有四個異常的高值或低值，與總共 13 個相關維度相比，仍然相對較少。此外，異常值星形圖顯示，資料中似乎存在不同組的國家，它們具有由各自星星形狀所反映的相似特徵。如果我們選擇用一種或多種“箱線圖異常值”來標記所有觀察結果，那麼剩下的（綠色）觀察結果似乎具有非常相似的特徵。但剩餘的國家數量非常有限，似乎不能代表世界上的國家群體。

然而，我們可以檢查在進一步的分析過程中排除某些“多維異常值”的影響。

雙變數分析

圖 7，所有變數相對於結核病患病率（y 軸）繪製。

現在，我們想要更好地瞭解我們感興趣的變數，即結核病患病率，與其他變數之間的關係，這些變數根據我們的目標被認為是解釋變數。在一個數據集中視覺化所有變數之間關係的一種方法是散點圖。在這種圖形中，所有變數都會彼此繪製。由於我們有 13 個感興趣的變數，這將為我們提供一個 13 x 13 的二維圖形顯示，這幾乎不允許在標準計算機顯示器上進行適當的顯示。此外，對角線上有空位，並且上三角形和下三角形中的資訊重複。因此，這種圖形只能以適當的方式用於最多八個變數。

圖 8，點選圖片檢視程式程式碼。

相反，我們只是將所有解釋變數對結核病進行繪圖，並將它們顯示在一個視窗中，該視窗顯示在 圖 7 中。該圖提供了推匯出資料之間關係的基本假設所需的必要資訊。

首先，可以看出，大多數觀測值似乎分佈在一個非常小的區域內，在大多數情況下是圖表的角落，而只有相對較小的一部分散佈在整個圖表的範圍內。為了更好地視覺化這一點，我們在繪圖中添加了一個維度，並計算了繪圖的二維密度估計。這可以在 圖 8 中看到，它以示例的形式顯示了“結核病”和“衛生設施”的二維密度估計。這進一步加強了我們分析前幾步中提到的想法。也就是說，可以根據可用的資訊/變數將這些國家劃分為不同的組。此外，解釋變數和結核病之間似乎存在不同的關係。這些關係將在我們分析的後續步驟中進行考慮。由於這些關係可能因子組而異，因此我們繼續嘗試在國家中找到同質組，並轉向在 多元分析部分 上發展關於關係的假設。

尋找組

由於我們已經看到了許多表明不同組存在的指標，因此我們將嘗試找到並解釋資料中可以找到的組。在我們使用現有的統計方法之前，我們想提一下對全球各國的一種常見區分。這是根據其“總體發展水平”將國家劃分為發達國家（通常與西歐國家、北美和日本同義），新興國家（如東南亞“四小龍”國家，以及大多數拉丁美洲國家），以及發展中國家（以前經常被描述為第三世界（儘管只有一個），因為這些國家是收入和生活水平最低的國家）。儘管這三種國家組別的區分並不是真正基於像我們這樣的資料，而是實際上還包含了更多經濟資料以及社會科學資料，但人們仍然期望找到類似於上面描述的組。現在，我們將使用聚類分析的統計方法來嘗試找到彼此之間差異儘可能大的組。

聚類分析

圖 9，點選圖片檢視程式程式碼及其用途說明。

聚類分析的目的是從一個異質的大型資料集中構建具有同質屬性的組。所使用的方法通常分為兩個步驟：選擇鄰近性度量，它檢查每對觀測值（物件）的相似性。然後定義相似性（鄰近性）度量來測量物件的接近程度。它們越接近，就越同質。以及選擇群組構建演算法，該演算法根據鄰近性度量將物件分配給群組，以便群組之間的差異變得很大，而群組中的觀測值儘可能接近。

在我們的分析中，我們選擇使用歐幾里得距離作為鄰近性度量，該距離是兩點之間的平方距離。但在這樣做之前，我們透過方差對資料進行了標準化，因為變數使用了不同的縮放比例。

我們的演算法是所謂的 Ward 聚類演算法，該演算法將那些不會過度增加給定異質性度量的組合並在一起。Ward 程式的目的是合併組，使這些組內部的變化不會過分增加：最終得到的組儘可能同質。我們在 圖 9 中的樹狀圖中看到了聚類序列的圖形表示。它顯示了觀測值、聚類序列以及聚類之間的距離。縱軸顯示了點的索引，而橫軸顯示了聚類之間的距離。

我們可以清楚地區分三個同質性相對較高的組（聚類）。最右側包含 108 個觀測值的最大的聚類代表發展中國家，中間包含 37 個觀測值的組代表新興國家，而最小的包含 18 個觀測值的組與發達國家相同。

此外，我們還計算了三個聚類均值的 PCP（平行座標圖），以直觀地顯示這些組之間的差異。綠線代表發達國家，紅線代表新興國家，藍線代表發展中國家。正如我們所預期的，可以觀察到兩個明顯相反的組。紅線（新興國家）接近藍線（發達國家），這似乎是一個合理的結論。

要獲取包含在不同聚類中的國家列表，請執行附在 圖 9 中的程式。

多元分析

如 雙變數分析 部分所述，可能存在結核病與我們資料集中包含的解釋變數之間的不同關係。還應提到，我們既沒有非常精深的醫學知識，也沒有從我們自己的經驗中瞭解高結核病患病率國家的狀況。因此，可能難以理解不同變數之間的關係。儘管如此，我們仍將對幾乎所有解釋變數進行一些假設，並看看它們是否成立。從 雙變數分析 部分的圖 5 中，我們發現 圖 11 中顯示的迴歸線（紅色，實線）非常接近點雲。這些關係可以用以下可能幼稚的方式解釋。

假設發展

圖 10，點選圖片檢視程式程式碼和說明。

• 結核病患病率與艾滋病相關死亡人數

這裡使用的函式形式（圖 10 和 圖 11），基於以下假設：如果結核病患病率上升，與艾滋病相關的死亡人數將呈指數增長。雖然這兩個變數相互關聯，但醫學專家可能會爭辯說，與艾滋病相關的死亡人數受結核病患病率的影響，而不是相反。然而，人們可以（從政治角度來看可能並不完全正確）認為，如果更多患有艾滋病和結核病的人死亡，那麼結核病感染人數就會下降。因此，我們假設該變數可以幫助解釋結核病患病率。

• 結核病患病率與瘧疾患病率

瘧疾和結核病之間似乎沒有線性關係。但是，如果我們排除了一些瘧疾病例非常嚴重的國家，我們可能會學到更多。這可以透過“paf”命令輕鬆實現。儘管如此，如以下表格中的 p 值所示，瘧疾患病率對結核病患病率沒有顯著影響。

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                 22178.097     1 22178.097       2.228   0.1375"
[ 5,] "Residuals                 1602701.069   161  9954.665"
[ 6,] "Total Variation           1624879.166   162 10030.118"
[ 7,] ""
[ 8,] "Multiple R      = 0.11683"
[ 9,] "R^2             = 0.01365"
[10,] "Adjusted R^2    = 0.00752"
[11,] "Standard Error  = 99.77307"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=         95.8129       8.1290       0.0000        11.787   0.0000"
[17,] "b[ 1,]=          0.0296       0.0198       0.1168         1.493   0.1375"

• 結核病患病率與女性使用安全套作為避孕工具

正如我們在 單變數分析 中提到的那樣，這個變數很難處理，因為安全套的相對使用率似乎不能說明性交過程中使用安全套的頻率。如果其他避孕措施的使用頻率不高，那麼安全套的相對使用率可能很高。因此，我們沒有對這兩個變數之間的關係做出假設。儘管如此，事實證明，在結核病患病率的簡單線性迴歸模型中，安全套使用率的係數與零顯著不同。

注意：如果我們在進一步分析中提到顯著性，我們始終指的是至少 5% 的 alpha！出於空間原因，我們沒有將所有迴歸輸出表格整合在一起。

圖 11，點選圖片檢視程式程式碼及其用途說明。

• 結核病患病率與獲得基本藥物

這裡的難點在於我們有分類資料。儘管如此，我們假設存線上性關係，這一點得到了顯著迴歸係數的證實。負相關是顯而易見的。

• 結核病患病率與受教育程度和識字率

儘管我們可能會遇到異方差性，但我們假設整個資料集存線上性關係。這一點也得到了顯著迴歸係數的證實。

• 結核病患病率與獲得衛生設施和清潔飲用水

同樣需要考慮異方差性。關於線性關係的假設得到了顯著 p 值的證實。

• 結核病患病率與 CO2 排放量

將二氧化碳排放量與肺結核患病率之間的關係解釋清楚並非易事。但如果我們將二氧化碳排放量視為一般經濟發展和生活水平的潛在因素，這種關係似乎更有意義。在圖 11（第三行，第一個元素）中假設和顯示的函式形式，是基於負邊際影響的假設，即，對於較低的二氧化碳排放量/生活水平，二氧化碳排放量/生活水平的微小增加對肺結核患病率的影響更大，並從一定水平開始逐漸減弱。

• 肺結核患病率與網際網路接入、個人電腦和電話普及率的關係。

這三個變數可以被理解為資訊獲取途徑。我們假設，在資訊總體水平較低的情況下，額外資訊將特別有價值。例如，透過媒體傳播的關於可以透過人體體液感染肺結核的簡單資訊。因此，在資訊總體水平較低的情況下，資訊對肺結核患病率的影響更大。如果人們已經獲得了大量新聞，額外的資訊可能會導致我們所說的資訊過載，即人們不再注意到這些資訊。

為了簡化起見，描述這四個變數之間關係的函式形式對於所有變數都相同。其依據基本上是所有變數都具有負邊際影響的假設，如上所述。這裡使用的函式形式為

$tub=\beta _{0}+\beta _{1}\cdot {\frac {1}{x^{0.3}}}$

最後四個（變換後的）變數的簡單線性迴歸模型的p值也顯著。並且，如您在下面的輸出表中所見，調整後的R^2始終相對較高。因此，我們將維持我們的假設。

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                781723.888     1781723.888     149.270   0.0000"
[ 5,] "Residuals                 843155.278   161  5236.989"
[ 6,] "Total Variation           1624879.166   162 10030.118"
[ 7,] ""
[ 8,] "Multiple R      = 0.69361"
[ 9,] "R^2             = 0.48110"
[10,] "Adjusted R^2    = 0.47787"
[11,] "Standard Error  = 72.36705"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=        -21.0144      11.3520       0.0000        -1.851   0.0660"
[17,] "b[ 1,]=        118.3640       9.6880       0.6936        12.218   0.0000"

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                605005.143     1605005.143      95.508   0.0000"
[ 5,] "Residuals                 1019874.023   161  6334.621"
[ 6,] "Total Variation           1624879.166   162 10030.118"
[ 7,] ""
[ 8,] "Multiple R      = 0.61020"
[ 9,] "R^2             = 0.37234"
[10,] "Adjusted R^2    = 0.36844"
[11,] "Standard Error  = 79.59033"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=          6.5870      11.3392       0.0000         0.581   0.5621"
[17,] "b[ 1,]=         25.3361       2.5925       0.6102         9.773   0.0000"

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                663303.291     1663303.291     111.059   0.0000"
[ 5,] "Residuals                 961575.874   161  5972.521"
[ 6,] "Total Variation           1624879.166   162 10030.118"
[ 7,] ""
[ 8,] "Multiple R      = 0.63892"
[ 9,] "R^2             = 0.40822"
[10,] "Adjusted R^2    = 0.40454"
[11,] "Standard Error  = 77.28209"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=        -18.9252      12.7351       0.0000        -1.486   0.1392"
[17,] "b[ 1,]=         35.7036       3.3879       0.6389        10.538   0.0000"

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                805435.082     1805435.082     158.248   0.0000"
[ 5,] "Residuals                 819444.083   161  5089.715"
[ 6,] "Total Variation           1624879.166   162 10030.118"
[ 7,] ""
[ 8,] "Multiple R      = 0.70405"
[ 9,] "R^2             = 0.49569"
[10,] "Adjusted R^2    = 0.49256"
[11,] "Standard Error  = 71.34224"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=        -25.7826      11.3957       0.0000        -2.262   0.0250"
[17,] "b[ 1,]=         61.4014       4.8810       0.7041        12.580   0.0000"

多元線性迴歸模型

現在，如果我們嘗試將所有解釋變數放入一個模型中會發生什麼？它們的影響在其他變數的影響方面是否仍然顯著？我們將嘗試在XploRe中實現的不同選擇過程，以計算擬合度最佳的模型，即調整後的$R^{2}$ 最佳的模型。

向前選擇模型

向前選擇選項從一個“良好”變數開始，計算簡單線性迴歸，然後逐步決定每個變數的加入是否可以改善模型的擬合度。

該過程產生了以下模型結果

$tub=\beta _{0}+\beta _{1}\cdot \log {(aids)}+\beta _{2}\cdot {\frac {1}{tel^{-0.3}}}+\epsilon$

Contents of out

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                910056.048     2455028.024     102.567   0.0000"
[ 5,] "Residuals                 700949.728   158  4436.391"
[ 6,] "Total Variation           1611005.776   160 10068.786"
[ 7,] ""
[ 8,] "Multiple R      = 0.75160"
[ 9,] "R^2             = 0.56490"
[10,] "Adjusted R^2    = 0.55939"
[11,] "Standard Error  = 66.60624"
[12,] ""
[13,] ""
[14,] "PARAMETERS         Beta         SE         StandB        t-test   P-value"
[15,] "________________________________________________________________________"
[16,] "b[ 0,]=        -29.2719      10.7465       0.0000        -2.724   0.0072"
[17,] "b[ 1,]=         12.7427       2.5019       0.3098         5.093   0.0000"
[18,] "b[ 2,]=         47.5180       5.2959       0.5458         8.973   0.0000"

向後剔除模型和逐步選擇模型

向後剔除過程從完整的多元迴歸模型開始，並逐步排除對模型擬合貢獻不大的變數。在我們案例中，逐步選擇模型產生了與向後剔除模型相同的結果。兩者都導致以下模型

$tub=\beta _{0}+\beta _{1}\cdot \log {(aids)}+\beta _{2}\cdot san+\beta _{3}\cdot wat+\beta _{4}\cdot {\frac {1}{tel^{-0.3}}}\ +\epsilon$

Contents of ANOVA

[ 1,] ""
[ 2,] "A  N  O  V  A                   SS      df     MSS       F-test   P-value"
[ 3,] "_________________________________________________________________________"
[ 4,] "Regression                963289.397     4240822.349      61.982   0.0000"
[ 5,] "Residuals                 606118.006 2e+02  3885.372"
[ 6,] "Total Variation              1611006   160 10068.786"
[ 7,] ""
[ 8,] "Multiple R      = 0.77327"
[ 9,] "R^2             = 0.59794"
[10,] "Adjusted R^2    = 0.61412"
[11,] "Standard Error  = 62.33275"

Contents of Summary

[ 1,] "Variables in the Equation for Y:"
[ 2,] " "
[ 3,] ""
[ 4,] "PARAMETERS         Beta         SE         StandB      t-test   P-value  Variable"
[ 5,] "  __________________________________________________________________________________"
[ 6,] "b[ 0,]=        155.7053      41.5609       0.0000      3.7464   0.0003   Constant   "
[ 7,] "b[ 1,]=         10.5762       2.3854       0.2571      4.4337   0.0000   X 1"
[ 8,] "b[ 2,]=         -0.8998       0.3050      -0.2283     -2.9500   0.0037   X 7"
[ 9,] "b[ 3,]=         -0.8339       0.4242      -0.1621     -1.9659   0.0511   X 8"
[10,] "b[ 4,]=         26.3803       6.6151       0.3030      3.9879   0.0001   X 12"

這並不是一個令人滿意的結果，因為該模型的解釋能力並沒有比大多數簡單迴歸模型高出多少。擬合不足的原因是什麼？這個問題將在我們的最終結論中得到解答。

結論

正如我們在分析過程中所見，有許多方法可以加深您對未知資料集的理解。雖然我們並沒有真正找到一個令人滿意的模型來完全解釋不同國家肺結核患病率的差異，但我們對資料集中的結構有了更深入的瞭解。我們已經看到了肺結核患病率與所有其他變數之間的單變數關係，並嘗試對其進行解釋。此外，我們在資料中找到了相當合理的組，這些組可以透過提供的程式單獨評估。

然而，多元分析（如多元迴歸）需要更復雜的方法。正如我們從整個資料集的相關矩陣中可以輕易看到的那樣，許多不同的變數彼此相關。這在某些情況下是顯而易見的，例如電話線、網際網路接入可能性和個人電腦方面。這些多重共線性問題使得多元迴歸相當困難，因為可以得到許多擬合度相似但解釋變數不同的模型。因此，我們應該嘗試找到一種方法來降低資料集的維度，例如透過因子分析。

最後，我們應該再次提到，我們的假設既沒有基於複雜的醫學專業知識，也沒有關於我們資料隨時間變化的任何資訊，而這些資訊可能有助於得出更好的假設，並可以用本文介紹的方法進行檢驗。

無論如何，我們留給了讀者自己，利用提供的程式繼續進行分析。例如，可以使用不同的聚類（透過程式 9 儲存）來重複異常值處理（使用程式 6）或雙變數分析（使用程式 11）等等。

參考文獻

[Härdle, Klinke, Müller 2000] Härdle, W.; Klinke, S.; Müller, M.: Xplore學習指南. Springer Verlag Berlin-Heidelberg, 2000

[Härdle, Simar 2003] Härdle, W.; Simar, L.: 應用多元統計分析. Springer Verlag Berlin-Heidelberg, 2003

[Hädle, Hlavka, Klinke 2000] Hädle, W.; Hlavka, Z.; Klinke, S.: XploRe應用指南. Springer Verlag Berlin-Heidelberg, 2000

聯合國統計司，網址為http://unstats.un.org/unsd/cdb/cdb_list_dicts.asp，訪問時間為2006年12月9日。

XploRe 幫助，網址為http://www.xplore-stat.de/help/_Xpl_Start.html