在下文中,我們將提供一些關於數值最佳化演算法的筆記。由於存在眾多方法 ,我們將只關注所謂的梯度方法 。我們之所以將此類方法作為考慮數值最佳化演算法的自然起點,主要有以下兩點原因。一方面,這些方法在該領域確實是主力軍,因此它們在實踐中的頻繁使用證明了它們在這裡的覆蓋範圍。另一方面,這種方法非常直觀,因為它在某種程度上從眾所周知的最優值性質 自然地推匯出。我們將特別關注該類方法的三個例子:牛頓方法 、最速下降法 以及可變度量方法 ,其中包括擬牛頓方法 。
在開始之前,我們要強調,似乎不存在“唯一”演算法,而特定演算法的效能總是取決於待解決的特定問題。因此,經驗和“試錯”在應用工作中非常重要。為了闡明這一點,我們將提供幾個應用程式,其中可以以圖形方式比較不同演算法的效能。此外,最後還提供了一個關於最大似然估計 的具體示例。尤其是對於統計學家和計量經濟學家 來說,最大似然估計可能是在實踐中必須依賴數值最佳化演算法的最重要示例。
任何數值最佳化演算法都需要解決找到函式的“可觀察”性質的問題,以便計算機程式知道何時達到解。由於我們處理的是最佳化問題,因此兩個眾所周知的結論似乎是進行這種性質推導的合理起點。
如果 f 可微,並且 x ⋆ {\displaystyle x^{\star }}
( 1 a ) D f ( x ⋆ ) = 0 {\displaystyle (1a)\quad Df(x^{\star })=0}
即雅可比矩陣 D f ( x ) {\displaystyle Df(x)}
以及
如果 f 二次可微,並且 x ⋆ {\displaystyle x^{\star }}
( 1 b ) x T D 2 f ( x ⋆ ) x ≥ 0 {\displaystyle (1b)\quad x^{T}D^{2}f(x^{\star })x\geq 0}
即海森矩陣 D 2 f ( x ) {\displaystyle D^{2}f(x)} 正半定 的。
在下文中,我們將始終用 x ⋆ {\displaystyle x^{\star }} x ⋆ {\displaystyle x^{\star }} x ⋆ {\displaystyle x^{\star }} f {\displaystyle f} g ( f ( x ⋆ ) ) {\displaystyle g(f(x^{\star }))} x ⋆ {\displaystyle x^{\star }} f ( x ) = x 3 {\displaystyle f(x)=x^{3}} D f ( 0 ) = D 2 f ( 0 ) = 0 {\displaystyle Df(0)=D^{2}f(0)=0} x ⋆ ≠ 0 {\displaystyle x^{\star }\neq 0} x ⋆ {\displaystyle x^{\star }}
如果 D f ( x ⋆ ) = 0 {\displaystyle Df(x^{\star })=0} x T D 2 f ( z ) x ≥ 0 , ∀ x ∈ R n {\displaystyle x^{T}D^{2}f(z)x\geq 0,\forall x\in \mathbb {R} ^{n}} z ∈ B ( x ⋆ , δ ) {\displaystyle z\in {\mathcal {B}}(x^{\star },\delta )} x ⋆ {\displaystyle x^{\star }}
證明:對於 x ∈ B ( x ⋆ , δ ) {\displaystyle x\in {\mathcal {B}}(x^{\star },\delta )} 令 z = x ⋆ + t ( x − x ⋆ ) ∈ B {\displaystyle z=x^{\star }+t(x-x^{\star })\in {\mathcal {B}}} 泰勒近似 得到: f ( x ) − f ( x ⋆ ) = 0 + 1 2 ( x − x ⋆ ) T D 2 f ( z ) ( x − x ⋆ ) ≥ 0 {\displaystyle f(x)-f(x^{\star })=0+{\frac {1}{2}}(x-x^{\star })^{T}D^{2}f(z)(x-x^{\star })\geq 0} 其中 B ( x ⋆ , δ ) {\displaystyle {\mathcal {B}}(x^{\star },\delta )} 表示以 x ⋆ {\displaystyle x^{\star }} 為中心的開球,即 B ( x ⋆ , δ ) = { x : | | x − x ⋆ | | ≤ δ } {\displaystyle {\mathcal {B}}(x^{\star },\delta )=\{x:||x-x^{\star }||\leq \delta \}} 對於 δ > 0 {\displaystyle \delta >0}
f ( x ) = x 3 {\displaystyle f(x)=x^{3}} D f ( x ⋆ = 0 ) = 0 {\displaystyle Df(x^{\star }=0)=0} x T D 2 f ( z ) x = 6 z x 2 ≱ 0 ( e . g . z = − δ 2 ) {\displaystyle x^{T}D^{2}f(z)x=6zx^{2}\not \geq 0\quad (e.g.\,\,z=-{\frac {\delta }{2}})}
以及
f ( x ) = x 4 {\displaystyle f(x)=x^{4}} D f ( x ⋆ = 0 ) = 0 {\displaystyle Df(x^{\star }=0)=0} x T D 2 f ( z ) x = 12 z 2 x 2 ≥ 0 ∀ z {\displaystyle x^{T}D^{2}f(z)x=12z^{2}x^{2}\geq 0\quad \forall z}
牢記這一小點,我們現在可以轉向數值最佳化程式。
以下所有演算法都將依賴於以下假設
(A1) 集合 N ( f , f ( x ( 0 ) ) = { x ∈ R n | f ( x ) ≤ f ( x ( 0 ) ) } {\displaystyle N(f,f(x^{(0)})=\{x\in \mathbb {R} ^{n}|f(x)\leq f(x^{(0)})\}} 緊湊 的。
其中 x ( 0 ) {\displaystyle x^{(0)}} 上確界 * 和其 *下確界 *。因此,*(A1)* 保證了在 N ( f , f ( x ( 0 ) ) {\displaystyle N(f,f(x^{(0)})} x ⋆ {\displaystyle x^{\star }} D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0} D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0}
這種方法的問題當然很普遍,因為 D ( f ( x ⋆ ) ) = 0 {\displaystyle D(f(x^{\star }))=0} 極大值和鞍點 也是成立的。因此,好的演算法應該確保極大值和鞍點都被排除為可能的解。極大值可以透過要求 f ( x ( k + 1 ) ) < f ( x ( k ) ) {\displaystyle f(x^{(k+1)}) 序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ( k + 1 ) = φ ( x ( k ) ) {\displaystyle x^{(k+1)}=\varphi (x^{(k)})} x ( k ) {\displaystyle x^{(k)}} x ( k + 1 ) {\displaystyle x^{(k+1)}}
方向 d ( k ) {\displaystyle d^{(k)}} 步長 σ ( k ) {\displaystyle \sigma ^{(k)}} 因此,我們可以選擇我們想要移動的方向以到達 x ( k + 1 ) {\displaystyle x^{(k+1)}} 以及 這種移動需要多遠。所以,如果我們選擇 d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}}
引理:如果 d ( k ) ∈ R n {\displaystyle d^{(k)}\in \mathbb {R} ^{n}} D f ( x ) T d ( k ) < 0 {\displaystyle Df(x)^{T}d^{(k)}<0} ∃ σ ¯ > 0 {\displaystyle \exists {\bar {\sigma }}>0}
f ( x + σ ( k ) d ( k ) ) < f ( x ) ∀ σ ∈ ( 0 , σ ¯ ) {\displaystyle f(x+\sigma ^{(k)}d^{(k)})<f(x)\quad \forall \sigma \in (0,{\bar {\sigma }})}
證明:因為 D f ( x ) T d ( k ) < 0 {\displaystyle Df(x)^{T}d^{(k)}<0} D f ( x ) T d ( k ) = lim σ → 0 f ( x + σ ( k ) d ( k ) ) − f ( x ) σ ( k ) {\displaystyle Df(x)^{T}d^{(k)}=\lim _{\sigma \rightarrow 0}{\frac {f(x+\sigma ^{(k)}d^{(k)})-f(x)}{\sigma ^{(k)}}}} f ( x + σ ( k ) d ( k ) ) < f ( x ) {\displaystyle f(x+\sigma ^{(k)}d^{(k)})<f(x)} σ ( k ) {\displaystyle \sigma ^{(k)}}
滿足此條件的方向向量 d ( k ) {\displaystyle d^{(k)}} 下降方向 。在實踐中,此引理允許我們使用以下程式來數值求解最佳化問題。
1. 定義序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ( k + 1 ) = x ( k ) + σ ( k ) d ( k ) {\displaystyle x^{(k+1)}=x^{(k)}+\sigma ^{(k)}d^{(k)}}
2. 從點 x ( k ) {\displaystyle x^{(k)}} d ( k ) {\displaystyle d^{(k)}}
3. 選擇一個步長 σ ( k ) {\displaystyle \sigma ^{(k)}} 收斂 。
4. 如果 | f ( x ( k + 1 ) ) − f ( x ( k ) ) | < ϵ {\displaystyle |f(x^{(k+1)})-f(x^{(k)})|<\epsilon } ϵ > 0 {\displaystyle \epsilon >0}
這個過程已經暗示了 d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} 引理 1 選擇的),也不能保證收斂到最小值。乍一看,這似乎有點令人費解。如果我們找到一個序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} k 趨於無窮大的極限中,我們應該找到解決方案。為什麼情況並非如此,可以從借鑑於 W. Alt (2002, p. 76) 的以下例子中看出。
考慮以下例子,它雖然明顯是下降的,但並不收斂。令準則函式由下式給出 f ( x ) = x 2 {\displaystyle f(x)=x^{2}} x ( 0 ) = 1 {\displaystyle x^{(0)}=1} d ( k ) = − 1 {\displaystyle d^{(k)}=-1} σ ( k ) = ( 1 2 ) k + 2 {\displaystyle \sigma ^{(k)}=({\frac {1}{2}})^{k+2}} { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}}
( 2 ) x ( k + 1 ) = x ( k ) + ( 1 2 ) k + 2 ( − 1 ) = x ( k − 1 ) − ( 1 2 ) k + 1 − ( 1 2 ) k + 2 = x ( 0 ) − ∑ j = 0 k ( 1 2 ) j + 2 . {\displaystyle (2)\quad x^{(k+1)}=x^{(k)}+({\frac {1}{2}})^{k+2}(-1)=x^{(k-1)}-\left({\frac {1}{2}}\right)^{k+1}-\left({\frac {1}{2}}\right)^{k+2}=x^{(0)}-\sum _{j=0}^{k}\left({\frac {1}{2}}\right)^{j+2}.}
注意 x ( k ) > 0 ∀ k {\displaystyle x^{(k)}>0\,\,\forall \,\,k} f ( x ( k + 1 ) ) < f ( x ( k ) ) ∀ k {\displaystyle f(x^{(k+1)})<f(x^{(k)})\,\,\forall \,\,k}
( 3 ) lim k → ∞ x ( k ) = lim k → ∞ x ( 0 ) − ∑ j = 0 k − 1 ( 1 2 ) j + 2 = lim k → ∞ 1 − 1 4 ( 1 − ( 1 2 ) k 1 2 ) = lim k → ∞ 1 2 + ( 1 2 ) k + 1 = 1 2 ≠ 0 = x ⋆ . {\displaystyle (3)\quad \lim _{k\rightarrow \infty }x^{(k)}=\lim _{k\rightarrow \infty }x^{(0)}-\sum _{j=0}^{k-1}\left({\frac {1}{2}}\right)^{j+2}=\lim _{k\rightarrow \infty }1-{\frac {1}{4}}\left({\frac {1-\left({\frac {1}{2}}\right)^{k}}{\frac {1}{2}}}\right)=\lim _{k\rightarrow \infty }{\frac {1}{2}}+\left({\frac {1}{2}}\right)^{k+1}={\frac {1}{2}}\neq 0=x^{\star }.}
這種不收斂的原因要歸咎於步長 σ ( k ) {\displaystyle \sigma ^{(k)}} k ,步長 x ( k + 1 ) − x ( k ) {\displaystyle x^{(k+1)}-x^{(k)}} d ( k ) {\displaystyle d^{(k)}}
這種聯絡的顯而易見的思路是要求實際下降與一階近似成正比,即選擇 σ ( k ) {\displaystyle \sigma ^{(k)}} c 1 > 0 {\displaystyle c_{1}>0}
( 4 ) f ( x ( k ) + σ ( k ) d ( k ) ) − f ( x ( k ) ) ≤ c 1 σ ( k ) D ( f ( x ( k ) ) ) d ( k ) < 0. {\displaystyle (4)\quad f(x^{(k)}+\sigma ^{(k)}d^{(k)})-f(x^{(k)})\leq c_{1}\sigma ^{(k)}D(f(x^{(k)}))d^{(k)}<0.}
請注意,我們仍然只關注下降方向,因此 D f ( x ( k ) ) T d ( k ) < 0 {\displaystyle Df(x^{(k)})^{T}d^{(k)}<0} N ( f , f ( x ( k ) ) ) {\displaystyle N(f,f(x^{(k)}))} 收斂 ,並且由 (4) 得出
( 5 ) lim k → ∞ σ ( k ) D ( f ( x ( k ) ) ) d ( k ) = 0. {\displaystyle (5)\quad \lim _{k\rightarrow \infty }\sigma ^{(k)}D(f(x^{(k)}))d^{(k)}=0.}
最後,我們希望選擇一個序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} lim k → ∞ D ( f ( x ( k ) ) ) = 0 {\displaystyle \lim _{k\rightarrow \infty }D(f(x^{(k)}))=0} lim k → ∞ D ( f ( x ( k ) ) ) = 0 {\displaystyle \lim _{k\rightarrow \infty }D(f(x^{(k)}))=0} σ ( k ) {\displaystyle \sigma ^{(k)}}
( 6 ) σ ( k ) ≥ − c 2 D f ( x ( k ) ) T d ( k ) | | d ( k ) | | 2 > 0 {\displaystyle (6)\quad \sigma ^{(k)}\geq -c_{2}{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||^{2}}}>0}
對於某個常數 c 2 > 0 {\displaystyle c_{2}>0}
( 7 ) f ( x ( k ) + σ ( k ) d ( k ) ) − f ( x ( k ) ) ≤ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 , c = c 1 c 2 {\displaystyle (7)\quad f(x^{(k)}+\sigma ^{(k)}d^{(k)})-f(x^{(k)})\leq -c\left({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}\right)^{2},\quad c=c_{1}c_{2}}
這裡, N ( f , f ( x ( k ) ) ) {\displaystyle N(f,f(x^{(k)}))} 緊緻性 保證了左側的 收斂 ,因此
( 8 ) lim k → ∞ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 = lim k → ∞ D f ( x ( k ) ) T d ( k ) | | d ( k ) | | = 0 {\displaystyle (8)\quad \lim _{k\rightarrow \infty }-c({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}})^{2}=\lim _{k\rightarrow \infty }{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}=0}
滿足 (4) 和 (6) 的步長被稱為 *有效步長*,並用 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}}
請注意,正是 (6) 的失效導致了示例 1 未收斂。將示例中的步長代入 (6) 得到 ( 6.1 ) σ ( k ) = ( 1 2 ) ( k + 2 ) ≥ − c 2 2 x ( k ) ( − 1 ) 1 = c 2 ⋅ 2 ( 1 2 + ( 1 2 ) k + 1 ) ⇔ 1 4 ( 1 + 2 ( k ) ) ≥ c 2 > 0 {\displaystyle (6.1)\quad \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{(k+2)}\geq -c_{2}{\frac {2x^{(k)}(-1)}{1}}=c_{2}\cdot 2({\frac {1}{2}}+\left({\frac {1}{2}})^{k+1}\right)\Leftrightarrow {\frac {1}{4(1+2^{(k)})}}\geq c_{2}>0}
因此,對於所有k ,沒有 常數 c 2 > 0 {\displaystyle c_{2}>0} σ ( k ) = ( 1 2 ) k + 1 {\displaystyle \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{k+1}}
( 6.2 ) lim k → ∞ x ( k + 1 ) = lim k → ∞ x ( 0 ) − 1 2 ∑ i ( 1 2 ) i = lim k → ∞ ( 1 2 ) k + 1 = 0 = x ⋆ , {\displaystyle (6.2)\quad \lim _{k\rightarrow \infty }x^{(k+1)}=\lim _{k\rightarrow \infty }x^{(0)}-{\frac {1}{2}}\sum _{i}\left({\frac {1}{2}}\right)^{i}=\lim _{k\rightarrow \infty }\left({\frac {1}{2}}\right)^{k+1}=0=x^{\star },}
即,收斂 確實發生了。此外,認識到此示例實際上滿足條件 (6),因為
( 6.3 ) σ ( k ) = ( 1 2 ) ( k + 1 ) ≥ − c 2 2 x ( k ) ( − 1 ) 1 = c 2 ⋅ 2 ( 1 2 ) k ⇔ 1 4 ≥ c 2 > 0. {\displaystyle (6.3)\quad \sigma ^{(k)}=\left({\frac {1}{2}}\right)^{(k+1)}\geq -c_{2}{\frac {2x^{(k)}(-1)}{1}}=c_{2}\cdot 2\left({\frac {1}{2}}\right)^{k}\Leftrightarrow {\frac {1}{4}}\geq c_{2}>0.}
我們已經論證過, σ ( k ) {\displaystyle \sigma ^{(k)}} d ( k ) {\displaystyle d^{(k)}} d ( k ) {\displaystyle d^{(k)}} σ ( k ) {\displaystyle \sigma ^{(k)}} 有效步長 意味著
( 8 ′ ) lim k → ∞ − c ( D f ( x ( k ) ) T d ( k ) | | d ( k ) | | ) 2 = lim k → ∞ D f ( x ( k ) ) T d ( k ) | | d ( k ) | | = 0. {\displaystyle (8')\quad \lim _{k\rightarrow \infty }-c({\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}})^{2}=\lim _{k\rightarrow \infty }{\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}=0.}
因此,“正確”的方向向量將保證 (8') 意味著
( 9 ) lim k → ∞ D f ( x ( k ) ) = 0 {\displaystyle (9)\quad \lim _{k\rightarrow \infty }Df(x^{(k)})=0}
因為 (9) 是所選序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} σ k {\displaystyle \sigma _{k}}
( 10 ) β ( k ) = D f ( x ( k ) ) T d ( k ) | | D f ( x ( k ) ) | | | | d ( k ) | | ⇔ β ( k ) | | D f ( x ( k ) ) | | = D f ( x ( k ) ) T d ( k ) | | d ( k ) | | {\displaystyle (10)\quad \beta ^{(k)}={\frac {Df(x^{(k)})^{T}d^{(k)}}{||Df(x^{(k)})||||d^{(k)}||}}\quad \Leftrightarrow \quad \beta ^{(k)}||Df(x^{(k)})||={\frac {Df(x^{(k)})^{T}d^{(k)}}{||d^{(k)}||}}}
根據 (8') 和 (10),我們知道
( 11 ) lim k → ∞ β ( k ) | | D f ( x ( k ) ) | | = 0. {\displaystyle (11)\quad \lim _{k\rightarrow \infty }\beta ^{(k)}||Df(x^{(k)})||=0.}
因此,如果我們從下方對 β ( k ) {\displaystyle \beta ^{(k)}} β ( k ) ≤ − δ < 0 {\displaystyle \beta ^{(k)}\leq -\delta <0}
( 12 ) lim k → ∞ β ( k ) | | D f ( x ( k ) ) | | = lim k → ∞ | | D f ( x ( k ) ) | | = lim k → ∞ D f ( x ( k ) ) = 0 , {\displaystyle (12)\quad \lim _{k\rightarrow \infty }\beta ^{(k)}||Df(x^{(k)})||=\lim _{k\rightarrow \infty }||Df(x^{(k)})||=\lim _{k\rightarrow \infty }Df(x^{(k)})=0,}
其中 (12) 給出了序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} x ⋆ {\displaystyle x^{\star }} β ( k ) {\displaystyle \beta ^{(k)}} d ( k ) {\displaystyle d^{(k)}} β ( k ) {\displaystyle \beta ^{(k)}} d ( k ) {\displaystyle d^{(k)}}
當考慮對 β ( k ) {\displaystyle \beta ^{(k)}} β ( k ) {\displaystyle \beta ^{(k)}}
β k = D ( f ( x ) ) d ( k ) | | D f ( x ( k ) ) | | | | d ( k ) | | = cos ( D f ( x ( k ) ) , d ( k ) ) {\displaystyle \beta _{k}={\frac {D(f(x))d^{(k)}}{||Df(x^{(k)})||||d^{(k)}||}}=\cos(Df(x^{(k)}),d^{(k)})}
我們有以下結果
鑑於 σ ( k ) {\displaystyle \sigma ^{(k)}} 是有效選擇的,並且 d ( k ) {\displaystyle d^{(k)}} 滿足
( 13 ) cos ( D f ( x ( k ) ) , d ( k ) ) = β k ≤ − δ < 0 {\displaystyle (13)\quad \cos(Df(x^{(k)}),d^{(k)})=\beta _{k}\leq -\delta <0}
我們有
( 14 ) lim k → ∞ D f ( x ( k ) ) → 0 {\displaystyle (14)\quad \lim _{k\rightarrow \infty }Df(x^{(k)})\rightarrow 0}
因此:如果 x ( k ) {\displaystyle x^{(k)}} 處的負梯度和方向 d ( k ) {\displaystyle d^{(k)}} 之間的角度始終小於直角,則會發生收斂。依賴於滿足 (13) 的 d ( k ) {\displaystyle d^{(k)}} 的方法被稱為梯度方法。
換句話說:只要不朝與梯度垂直的方向移動,並且如果步長選擇有效,梯度方法 就可以保證收斂到解 x ⋆ {\displaystyle x^{\star }}
現在,讓我們探索這一類別中的三種特定演算法,它們在各自選擇的 d ( k ) {\displaystyle d^{(k)}}
牛頓法 根 ,因此很容易應用於最佳化問題。牛頓法的主要思想是線性化方程組,得到
( 15 ) g ( x ) = g ( x ^ ) + D g ( x ^ ) T ( x − x ^ ) = 0. {\displaystyle (15)\quad g(x)=g({\hat {x}})+Dg({\hat {x}})^{T}(x-{\hat {x}})=0.}
(15) 可以很容易地求解出 x ,因為解只是(假設 D g ( x ^ ) T {\displaystyle Dg({\hat {x}})^{T}} 非奇異 的)
( 16 ) x = x ^ − [ D g ( x ^ ) T ] − 1 g ( x ^ ) . {\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}
為了我們的目的,我們選擇 g ( x ) {\displaystyle g(x)} D f ( x ) {\displaystyle Df(x)}
( 17 ) d N ( k ) = x ( k + 1 ) − x ( k ) = − [ D 2 f ( x ( k ) ) ] − 1 D f ( x ( k ) ) {\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}
其中 d N ( k ) {\displaystyle d_{N}^{(k)}} 牛頓方向 。
分析(17)揭示了牛頓法的主要性質
如果 D 2 f ( x ( k ) ) {\displaystyle D^{2}f(x^{(k)})} 正定 ,則 d N k {\displaystyle d_{N}^{k}} 引理1 意義上的下降方向。 牛頓法 使用一階和 二階導數的區域性資訊來計算 d N k {\displaystyle d_{N}^{k}} ( 18 ) x ( k + 1 ) = x ( k ) + d N ( k ) {\displaystyle (18)\quad x^{(k+1)}=x^{(k)}+d_{N}^{(k)}}
牛頓法 使用 σ ( k ) = 1 {\displaystyle \sigma ^{(k)}=1} 不 一定是一種按照引理1 意義上的下降方法。原因是固定步長 σ ( k ) = 1 {\displaystyle \sigma ^{(k)}=1} 引理1 中給出的臨界步長 σ k ¯ {\displaystyle {\bar {\sigma _{k}}}}
該方法可能很耗時,因為在每一步k 中計算 [ D 2 f ( x ( k ) ) ] − 1 {\displaystyle [D^{2}f(x^{(k)})]^{-1}} s 步更新一次Hessian,或者可以依賴於區域性近似 。這被稱為擬牛頓法 ,將在關於可變度量法 的部分中討論。 為了確保該方法為下降方法,可以使用一個有效的步長 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} ( 19 ) x ( k + 1 ) = x ( k ) − σ E ( k ) d N ( k ) = x ( k ) − σ E ( k ) [ D 2 f ( x k ) ] − 1 D f ( x ( k ) ) {\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}
另一種常用的方法是最速下降法 d ( k ) {\displaystyle d^{(k)}} f 的下降最大。儘管這個過程乍一看很合理,但它實際上使用的資訊比牛頓法 少,因為它忽略了Hessian關於函式曲率的資訊。特別是在下面的應用中,我們將看到幾個關於這個問題的例子。
最速下降法 的方向向量由下式給出:
( 20 ) d S D ( k ) = a r g m a x d : | | d | | = r { − D f ( x ( k ) ) T d } = a r g m i n d : | | d | | = r { D f ( x ( k ) ) T d } = − r D f ( x ) | | D f ( x ) | | {\displaystyle (20)\quad d_{SD}^{(k)}=argmax_{d:||d||=r}\{-Df(x^{(k)})^{T}d\}=argmin_{d:||d||=r}\{Df(x^{(k)})^{T}d\}=-r{\frac {Df(x)}{||Df(x)||}}}
證明:根據柯西-施瓦茨不等式 ,可以得到
( 21 ) D f ( x ) T d | | D f ( x ) | | | | d | | ≥ − 1 ⇔ D f ( x ) T d ≥ − r | | D f ( x ) | | . {\displaystyle (21)\quad {\frac {Df(x)^{T}d}{||Df(x)||||d||}}\geq -1\quad \Leftrightarrow \quad Df(x)^{T}d\geq -r||Df(x)||.}
顯然 (21) 在 d ( k ) = d S D ( k ) {\displaystyle d^{(k)}=d_{SD}^{(k)}} 下成立,如 (20) 所示。
特別要注意的是,對於 r = | | D f ( x ) | | {\displaystyle r=||Df(x)||} d S D ( k ) = − D f ( x ( k ) ) {\displaystyle d_{SD}^{(k)}=-Df(x^{(k)})} 牛頓法 相比,最速下降法 沒有使用固定的步長,而是選擇了一個有效的步長 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} 最速下降法 定義了序列 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}}
( 22 ) x ( k + 1 ) = x ( k ) + σ E ( k ) d S D ( k ) , {\displaystyle (22)\quad x^{(k+1)}=x^{(k)}+\sigma _{E}^{(k)}d_{SD}^{(k)},}
其中 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}} d S D ( k ) {\displaystyle d_{SD}^{(k)}}
對於 d S D ( k ) = − r D f ( x ) | | D f ( x ) | | {\displaystyle d_{SD}^{(k)}=-r{\frac {Df(x)}{||Df(x)||}}} 引理 1 所述,因為 D f ( x ) T d S D ( k ) = D f ( x ) T ( − r D f ( x ) | | D f ( x ) | | ) = − r | | D f ( x ) | | D f ( x ) T D f ( x ) < 0. {\displaystyle Df(x)^{T}d_{SD}^{(k)}=Df(x)^{T}\left(-r{\frac {Df(x)}{||Df(x)||}}\right)=-{\frac {r}{||Df(x)||}}Df(x)^{T}Df(x)<0.}
最速下降法 僅在區域性上是合理的,因為它忽略了二階資訊。特別是當目標函式很平坦(即解 x ⋆ {\displaystyle x^{\star }} 由於它不需要海森矩陣,因此最速下降法 的計算和實現很容易且快速。 牛頓法 和最速下降法 都屬於可變度量法 類的一般方法。此類方法依賴於更新公式
( 23 ) x k + 1 = x k − σ E ( k ) [ A k ] − 1 D f ( x k ) . {\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}
如果 A k {\displaystyle A^{k}} 對稱 且 正定 矩陣,(23) 定義了一個下降方法,因為 [ A k ] − 1 {\displaystyle [A^{k}]^{-1}} A k {\displaystyle A^{k}} 譜分解
( 24 ) A k = Γ Λ Γ T {\displaystyle (24)\quad A^{k}=\Gamma \Lambda \Gamma ^{T}}
其中 Γ {\displaystyle \Gamma } Λ {\displaystyle \Lambda } 特徵向量 和 特徵值 的矩陣。如果 A k {\displaystyle A^{k}} λ i {\displaystyle \lambda _{i}} λ i − 1 {\displaystyle \lambda _{i}^{-1}} [ A k ] − 1 = Γ Λ − 1 Γ T {\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}} d ( k ) = [ A k ] − 1 D f ( x k ) {\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}
( 25 ) D f ( x k ) T d ( k ) = − D f ( x k ) T [ A k ] − 1 D f ( x k ) ≡ − v T [ A k ] − 1 v ≤ 0 , {\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}
即該方法確實是下降的。到目前為止,我們還沒有指定矩陣 A k {\displaystyle A^{k}} 可變度量法 恰好與最速下降法 和牛頓法 分別一致。
對於 A k = I {\displaystyle A^{k}={\mathcal {I}}} I {\displaystyle {\mathcal {I}}} 單位矩陣 ),可以得出 ( 22 ′ ) x k + 1 = x k − σ E ( k ) D f ( x k ) {\displaystyle (22')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}Df(x^{k})}
這僅僅是 *最速下降法*。
對於 A k = D 2 f ( x k ) {\displaystyle A^{k}=D^{2}f(x^{k})} ( 19 ′ ) x k + 1 = x k − σ E ( k ) [ D 2 f ( x k ) ] − 1 D f ( x k ) {\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}
這僅僅是使用步長 σ E ( k ) {\displaystyle \sigma _{E}^{(k)}}
對於 *變數度量法* 而言,另一個自然的候選方法是 *擬牛頓法*。與標準 *牛頓法* 相比,它使用了一種有效的步長,使其成為一種下降方法,並且與 *最速下降法* 相比,它沒有完全忽略有關函式曲率的區域性資訊。因此,*擬牛頓法* 由矩陣 A k {\displaystyle A^{k}}
A k {\displaystyle A^{k}} D 2 f ( x k ) {\displaystyle D^{2}f(x^{k})} 更新 A k → A k + 1 {\displaystyle A^{k}\rightarrow A^{k+1}} 為了確保第一個要求, A k + 1 {\displaystyle A^{k+1}}
( 26 ) A k + 1 ( x ( k + 1 ) − x ( k ) ) = D f ( x ( k + 1 ) ) − D f ( x ( k ) ) {\displaystyle (26)\quad A^{k+1}(x^{(k+1)}-x^{(k)})=Df(x^{(k+1)})-Df(x^{(k)})}
因為所有滿足 (26) 的 A k {\displaystyle A^{k}} g ( x ) {\displaystyle g(x)}
( 27 ) g ( x ) = f ( x k + 1 ) + D f ( x k + 1 ) T ( x − x k + 1 ) + 1 2 ( x − x k + 1 ) T A k + 1 ( x − x k + 1 ) . {\displaystyle (27)\quad g(x)=f(x^{k+1})+Df(x^{k+1})^{T}(x-x^{k+1})+{\frac {1}{2}}(x-x^{k+1})^{T}A^{k+1}(x-x^{k+1}).}
那麼很明顯, g ( x k + 1 ) = f ( x k + 1 ) {\displaystyle g(x^{k+1})=f(x^{k+1})} D g ( x k + 1 ) = D f ( x k + 1 ) {\displaystyle Dg(x^{k+1})=Df(x^{k+1})} g ( x ) {\displaystyle g(x)} f ( x ) {\displaystyle f(x)} x ( k + 1 ) {\displaystyle x^{(k+1)}} g ( x ) {\displaystyle g(x)} x ( k ) {\displaystyle x^{(k)}} A k + 1 {\displaystyle A^{k+1}} x ( k ) {\displaystyle x^{(k)}}
( 28 ) D g ( x k ) = D f ( x k + 1 ) − A k + 1 ( x k + 1 − x k ) {\displaystyle (28)\quad Dg(x^{k})=Df(x^{k+1})-A^{k+1}(x^{k+1}-x^{k})}
很明顯, D g ( x k ) = D f ( x k ) {\displaystyle Dg(x^{k})=Df(x^{k})} A k + 1 {\displaystyle A^{k+1}} 擬牛頓方程 。但隨後可以得出
( 29 ) A k + 1 ( x k + 1 − x k ) = D f ( x k + 1 ) − D g ( x k ) = D f ( x k + 1 ) − D f ( x k ) = D 2 f ( λ x ( k ) + ( 1 − λ ) x ( k + 1 ) ) ( x k + 1 − x k ) . {\displaystyle (29)\quad A^{k+1}(x^{k+1}-x^{k})=Df(x^{k+1})-Dg(x^{k})=Df(x^{k+1})-Df(x^{k})=D^{2}f(\lambda x^{(k)}+(1-\lambda )x^{(k+1)})(x^{k+1}-x^{k}).}
因此,只要 x ( k + 1 ) {\displaystyle x^{(k+1)}} x ( k ) {\displaystyle x^{(k)}} A k + 1 {\displaystyle A^{k+1}} D 2 f ( x ( k ) ) {\displaystyle D^{2}f(x^{(k)})}
現在讓我們來談談第二個要求,即 A k {\displaystyle A^{k}} BFGS 演算法 { x ( k ) } k {\displaystyle \{x^{(k)}\}_{k}} { D f ( x ( k ) ) } k {\displaystyle \{Df(x^{(k)})\}_{k}} A ( k + 1 ) {\displaystyle A^{(k+1)}} x 序列和梯度序列即可。作為 BFGS 演算法的起點,可以提供任何正定矩陣(例如,單位矩陣或在 x ( 0 ) {\displaystyle x^{(0)}} BFGS 更新公式 由下式給出
( 30 ) A k = A k − 1 − ( A k − 1 ) T γ k − 1 T γ k − 1 A k − 1 γ k − 1 T A k − 1 γ k − 1 + Δ k − 1 Δ k − 1 T Δ k − 1 T γ k − 1 {\displaystyle (30)\quad A^{k}=A^{k-1}-{\frac {(A^{k-1})^{T}\gamma _{k-1}^{T}\gamma _{k-1}A^{k-1}}{\gamma _{k-1}^{T}A^{k-1}\gamma _{k-1}}}+{\frac {\Delta _{k-1}\Delta _{k-1}^{T}}{\Delta _{k-1}^{T}\gamma _{k-1}}}}
其中 Δ k − 1 = D f ( x ( k ) ) − D f ( x ( k − 1 ) ) {\displaystyle \Delta _{k-1}=Df(x^{(k)})-Df(x^{(k-1)})} γ k − 1 = x ( k ) − x ( k − 1 ) {\displaystyle \gamma _{k-1}=x^{(k)}-x^{(k-1)}} A k {\displaystyle A^{k}} 變尺度法 所要求的那樣,是下降的。
它使用關於 f ( x ) {\displaystyle f(x)} A k {\displaystyle A^{k}} D 2 f ( x ) {\displaystyle D^{2}f(x)} 儘管如此,它確保了簡單快速的更新(例如,透過 BFGS 演算法),因此它比標準牛頓法更快。 它是一種下降方法,因為 A k {\displaystyle A^{k}} 它相對容易實現,因為 BFGS 演算法在大多數數值或統計軟體包中都可用。 為了比較這些方法並說明演算法之間的差異,我們現在將評估最速下降法 、標準牛頓法 和擬牛頓法 在有效步長下的效能。我們使用該領域中的兩個經典函式,即 Himmelblau 函式和 Rosenbrock 函式。
Himmelblau 函式由下式給出
( 31 ) f ( x , y ) = ( x 2 + y − 11 ) 2 + ( x + y 2 − 7 ) 2 {\displaystyle (31)\quad f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}}
這個四階多項式有四個極小值,四個鞍點和一個極大值,因此演算法有足夠的失敗可能性。在下圖中,我們顯示了 等高線圖 和函式的 3D 圖,用於不同的起始值。
在圖 1 中,我們顯示了函式以及所有三種方法在起始值為 ( 2 , − 4 ) {\displaystyle (2,-4)} 最速下降法 的不同方向向量造成的——透過忽略關於曲率的資訊,它選擇的方向與兩個牛頓法 完全不同(尤其是在圖 1 的右面板中)。
圖 1:兩個牛頓法收斂到相同的極小值,而最速下降法收斂到不同的極小值。 現在考慮起始值為 ( 4.5 , − 0.5 ) {\displaystyle (4.5,-0.5)} 所有 方法都找到了不同的解。最速下降法 找到的解與兩個牛頓法 不同,這並不令人驚訝。但是,兩個牛頓法 收斂到不同的解,這表明了步長 σ {\displaystyle \sigma } 擬牛頓法 在第一次迭代中選擇一個有效的步長,兩種方法在第一次迭代後的所有迭代中都有不同的步長和 方向向量。從圖中可以看到:結果可能非常重要。
圖 2:即使所有方法都找到了不同的解。 Rosenbrock 函式由下式給出
( 32 ) f ( x , y ) = 100 ( y − x 2 ) 2 + ( 1 − x ) 2 {\displaystyle (32)\quad f(x,y)=100(y-x^{2})^{2}+(1-x)^{2}\ }
雖然這個函式只有一個極小值,但它對於最佳化問題來說是一個有趣的函式。原因是這個 U 形函式的谷非常平坦(參見圖 3 和 4 的右面板)。對於 計量經濟學家 來說,這個函式可能很有趣,因為在最大似然估計的情況下,平坦的準則函式經常出現。因此,在下面圖 3 和 4 中顯示的結果對於具有此問題的函式來說似乎是相當通用的。
我使用這個函式和所採用的演算法的經驗是,圖 3(給定一個初始值為 ( 2 , − 5 ) {\displaystyle (2,-5)}
圖 3:所有方法都找到了相同的解,但最速下降法波動很大。 圖 4 考慮了初始值為 ( − 2 , − 2 ) {\displaystyle (-2,-2)} [ D f ( x ( k ) ) ] − 1 D f ( x ( k ) ) ) {\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}
圖 2:由於固定步長,牛頓法越界。 對於計量經濟學家和統計學家,**最大似然估計器**可能是數值最佳化演算法最重要的應用。因此,我們將簡要介紹估計程式如何適應上述框架。
像往常一樣,令
( 33 ) f ( Y | X ; θ ) {\displaystyle (33)\quad f(Y|X;\theta )}
是給定 X 時的 Y 的**條件密度**,引數為 θ {\displaystyle \theta }
( 34 ) l ( θ ; Y | X ) {\displaystyle (34)\quad l(\theta ;Y|X)}
是引數 θ {\displaystyle \theta }
如果我們假設資料是**獨立同分布 (iid)**,那麼樣本對數似然函式為
( 35 ) L ( θ ; Y 1 , … , Y N ) = ∑ i N L ( θ ; Y i ) = ∑ i N log ( l ( θ ; Y i ) ) . {\displaystyle (35)\quad {\mathcal {L}}(\theta ;Y_{1},\dots ,Y_{N})=\sum _{i}^{N}{\mathcal {L}}(\theta ;Y_{i})=\sum _{i}^{N}\log(l(\theta ;Y_{i})).}
因此,最大似然估計歸結為對引數 θ {\displaystyle \theta } { θ ( k ) } k {\displaystyle \{\theta ^{(k)}\}_{k}}
( 36 ) D θ L ( θ ( k + 1 ) ) = D θ L ( θ ( k ) ) + D θ θ L ( θ ( k ) ) ( θ ( k + 1 ) − θ ( k ) ) = 0 ⇔ θ ( k + 1 ) = θ ( k ) − [ D θ θ L ( θ ( k ) ) ] − 1 D θ L ( θ ( k ) ) {\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}
D θ L {\displaystyle D_{\theta }{\mathcal {L}}} D θ θ L {\displaystyle D_{\theta \theta }{\mathcal {L}}} θ {\displaystyle \theta } [ D θ θ L ( θ ( k ) ) ] − 1 D θ L ( θ ( k ) ) {\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})} θ {\displaystyle \theta }
假設一個簡單的線性模型
( 37 a ) Y i = β 1 + β x X i + U i {\displaystyle (37a)\quad Y_{i}=\beta _{1}+\beta _{x}X_{i}+U_{i}}
其中 θ = ( β 1 , β 2 ) ′ {\displaystyle \theta =(\beta _{1},\beta _{2})'} Y 的條件分佈由U 的分佈決定,即
( 37 b ) p ( Y i − β 1 − β x X i ) ≡ p ∣ X i ( Y i ) = p ( U i ) , {\displaystyle (37b)\quad p(Y_{i}-\beta _{1}-\beta _{x}X_{i})\equiv p_{\mid X_{i}}(Y_{i})=p(U_{i}),}
其中 p {\displaystyle p} 密度函式 。一般來說,最大化 (35) 沒有閉合形式解(至少如果U 恰好不是 正態分佈 ),因此必須使用數值方法。因此,假設U 服從 學生 t 分佈 ,自由度為m 自由度 ,因此 (35) 由下式給出
( 38 ) L ( θ ; Y ∣ X ) = ∑ log ( Γ ( m + 1 2 ) π m Γ ( m 2 ) ( 1 + ( y i − x i T β ) 2 m ) − m + 1 2 ) {\displaystyle (38)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=\sum \log \left({\frac {\Gamma ({\frac {m+1}{2}})}{{\sqrt {\pi m}}\Gamma ({\frac {m}{2}})}}(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}})^{-{\frac {m+1}{2}}}\right)}
我們只是使用了t分佈密度函式的定義。(38)可以簡化為
( 39 ) L ( θ ; Y ∣ X ) = N [ log ( Γ ( m + 1 2 ) ) − log ( π m Γ ( m 2 ) ) ] − m + 1 2 ∑ log ( 1 + ( y i − x i T β ) 2 m ) {\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}
所以(如果我們假設自由度m 是已知的)
( 40 ) argmax { L ( θ ; Y ∣ X ) } = argmax { − m + 1 2 ∑ log ( 1 + ( y i − x i T β ) 2 m ) } = argmin { ∑ log ( 1 + ( y i − x i T β ) 2 m ) } . {\displaystyle (40)\quad {\textit {argmax}}\left\{{\mathcal {L}}(\theta ;Y_{\mid X})\right\}={\textit {argmax}}\left\{-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)\right\}={\textit {argmin}}\left\{\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)\right\}.}
使用準則函式
( 41 ) f ( β 1 , β 2 ) = ∑ log ( 1 + ( y i − β 1 − β 2 x i ) 2 m ) {\displaystyle (41)\quad f(\beta _{1},\beta _{2})=\sum \log \left(1+{\frac {(y_{i}-\beta _{1}-\beta _{2}x_{i})^{2}}{m}}\right)}
上述方法可以很容易地應用於計算最大似然估計量 ( β ^ 1 , M L , β ^ 2 , M L ) {\displaystyle ({\hat {\beta }}_{1,ML},{\hat {\beta }}_{2,ML})}
Alt, W. (2002): "Nichtlineare Optimierung", Vieweg: Braunschweig/Wiesbaden
Härdle, W. and Simar, L. (2003): "Applied Multivariate Statistical Analysis", Springer: Berlin Heidelberg
Königsberger, K. (2004): "分析 I", 施普林格出版社: 柏林 海德堡
Ruud, P. (2000): "經典計量經濟學理論", 牛津大學出版社: 紐約 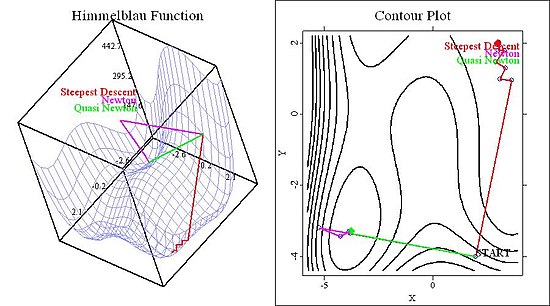




















































































![{\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/973ad4b1a68c0301124de9a8e4a9f5dcf2ede103)

![{\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f590fdfab4360315b24683a209d394d474d8d5)






![{\displaystyle [D^{2}f(x^{(k)})]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f24df6687d0360e41c29464f4aaf177e9314f9)
![{\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e7b82c56b6571dc71773a1301041f3e514bb0be)









![{\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b5580a0328e0fc4cb23c05d2aaa2dfb757e774)

![{\displaystyle [A^{k}]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6caa38bd6a32cf081b1e8379b42ccafdeaf56056)





![{\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0bb61f96e4008fe7ac42ddae42174a1cbc74f22)
![{\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd88606c2704c7ca9ba41fbff98dc6196d731f1)
![{\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19c3cfc50845559d027b7a787662c23b8209bdba)




![{\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e585e07182f56dfbe1ebb268e5b1feba19cac6e)























![{\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60231e722c13de70156e005a9956e01b4895cda1)





![{\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27be895a860dcd9530a4d300fdc8fa7f7e7f9e3c)


![{\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1bb702f696e4c7c16d636cdafdbf51382f32bfd)





![{\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ab57a856625145f8bd9be4f656dba107baf35a)


