三維電子顯微鏡/3D 重建
外觀
< 三維電子顯微鏡

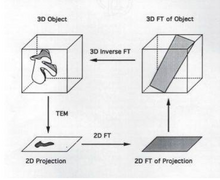



在透射電子顯微鏡中,3D 重建的目標是將 2D 投影轉換為其 3D 體積。這使得可以視覺化樣本中的微小結構。重建 2D 投影至關重要,因為從投影本身獲得的資訊有限。
投影發生在將 3D 影像拍攝並將其點放置在 2D 平面上時。2D 平面中的每個點對應於 3D 體積中的一個切片,並且基於拉東定理。可以獲得 3D 體積,獲取 2D 投影,隨後對投影進行傅立葉變換,並使用投影的傅立葉變換來獲得 3D 體積的“切片”。此後,可以對“切片”進行逆傅立葉變換,得到 3D 體積。
在進行重建之前,有必要知道粒子朝哪個方向。可以使用粒子的尤拉角來確定粒子的方向。尤拉角可以透過兩種方式定義。根據第一個定義,可以使用緯度、經度和粒子位置的旋轉來確定方向。第二個定義考慮了 z 軸和 x 軸。使用 Z 軸確定初始位置。接下來,旋轉粒子,並從新的 X 軸推匯出方向。第三個也是最後一個計算基於新的 Z 軸的位置,它已經繞其 x 軸旋轉。
反投影基本上是拉東變換的逆變換。它是一個將 2D 投影轉換為 3D 模型的過程。它是唯一可用於此目的的方法。反投影透過獲取每個檢視並將其沿著獲取它的相同路徑進行塗抹來重建影像(圖 1)。由此產生的結果是正確影像的模糊版本(Voss 2013)[1]。
獲得 3D 重建後,重要的是確定重建質量。這可以透過使用傅立葉殼相關性來完成。基本上,粒子集被分成一個偶數子集和一個奇數子集,其中為每個子集計算一個結構。然後將每個子集反投影以獲得每個子集的體積。由於目標是確定重建的質量,因此資料被分成傅立葉空間中的環,每個環代表不同的解析度。然後,根據其頻率計算偶數子集結構與奇數子集結構之間的相關係數。

- ↑ Voss, Neil. 3D 重建。蛋白質結構 464。羅斯福大學,沙弗堡,伊利諾伊州。2013 年 10 月 25 日。講座。
