介值定理是微積分中的一個基本定理。該定理指出,如果一個函式  在閉區間
在閉區間 ![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842) 上是連續的,那麼對於任何在
上是連續的,那麼對於任何在  和
和  之間定義的任何值
之間定義的任何值  ,都至少存在一個值
,都至少存在一個值  使得
使得  。
。
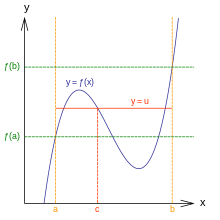 介值定理:f(x) 在 [a, b] 上是連續的,存在至少一個定義在 (a, b) 上的值 c,使得 f(c) = y。
介值定理:f(x) 在 [a, b] 上是連續的,存在至少一個定義在 (a, b) 上的值 c,使得 f(c) = y。
陳述:如果一個函式  在
在 ![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842) 上是連續的,那麼對於任何在
上是連續的,那麼對於任何在  和
和  之間的每個
之間的每個  ,都至少存在一個值
,都至少存在一個值  使得
使得  。
。
證明:假設  是
是 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上的連續函式,並且
上的連續函式,並且 
考慮一個函式  定義
定義  的目的是研究
的目的是研究  相對於值
相對於值  的行為。
的行為。
由於 在
在![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上連續,而
上連續,而 是一個常數,
是一個常數, 也是在
也是在![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842) 上連續,因為兩個連續函式的差是連續的。
上連續,因為兩個連續函式的差是連續的。
現在, [因為
[因為 並且
並且 ]
]
或者,

同理,
由於 是連續的,並且
是連續的,並且 定義在
定義在 軸下方,而
軸下方,而 定義在
定義在 軸上方,因此在區間
軸上方,因此在區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 中至少存在一個點
中至少存在一個點 ,使得
,使得 。
。
因此,在點  ,
,
∴ 存在至少一個點  在區間
在區間 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 中,使得
中,使得  [已證明]
[已證明]



![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)















