 這裡
這裡 
餘弦定理解釋了三角形邊長和一個角之間的關係。該定理指出,對於任意三角形  ,如果
,如果  ,
, ,
, 和
和  ,則
,則  。對於
。對於  是一個直角三角形,並且
是一個直角三角形,並且  ,我們之前已經將其證明為勾股定理。
,我們之前已經將其證明為勾股定理。
在任何三角形中,一條邊長的平方等於其他兩條邊長的平方和減去這兩條邊長乘積的兩倍以及它們所夾角的餘弦值的差。
假設, 是一個三角形,其中
是一個三角形,其中 

 和
和  需要證明的是,
需要證明的是, 。
。
讓我們將線段  延長至
延長至  (僅適用於鈍角三角形),其中
(僅適用於鈍角三角形),其中  。假設
。假設  以及
以及  .
.
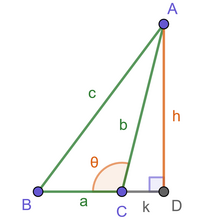 證明角為
證明角為  的餘弦定律的構造。
的餘弦定律的構造。
根據勾股定理,我們可以說,對於 

類似地,對於三角形 


 .
.
我們將使用這個值進行進一步的證明。但現在,讓我們確定三角形的一些三角函式值。
這裡, .
.
因此,
或者,
![{\displaystyle =b[\cos(\pi )\cdot cos(\theta )+\sin(\pi )\cdot \sin(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da982b5b73a75c5f627c5c65f72c819bcdee6e4)

現在, .
.
 . [證明完畢]
. [證明完畢]
 證明餘弦定理對於角度
證明餘弦定理對於角度 的構造。
的構造。
就像我們之前證明的那樣,根據勾股定理,我們可以說,對於

類似地,對於三角形


 .
.
這裡, .
.
所以,

現在, .
.
 . [證明完畢]
. [證明完畢]
[注意:無論三角形是什麼,公式  都適用。]
都適用。]






























![{\displaystyle =b[\cos(\pi )\cdot cos(\theta )+\sin(\pi )\cdot \sin(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da982b5b73a75c5f627c5c65f72c819bcdee6e4)










