交通地理與網路科學/圖論

改編自維基百科文章[1]

圖論是研究圖，一種用於對來自特定集合的物件之間的成對關係進行建模的數學結構。在此上下文中，“圖”指的是一組頂點或“節點”以及連線頂點對的一組邊。圖可以是無向的，這意味著與每條邊關聯的兩個頂點之間沒有區別，或者它的邊可以有向地從一個頂點指向另一個頂點；請參閱此處以瞭解更詳細的定義以及其他常用圖型別的變化。

請參考此處以瞭解圖論中的基本定義。

應用

圖是自然和人造結構中最普遍的模型之一。它們可用於對物理、生物和社會系統中的許多關係和過程動態進行建模。許多實際應用問題可以用圖來表示。

在計算機科學中，圖用於表示通訊網路、資料組織、計算裝置、計算流程等。一個實際例子：網站的連結結構可以用有向圖來表示。頂點是網站上可用的網頁，如果且僅當頁面A包含指向頁面B的連結時，從頁面A到頁面B才存在有向邊。類似的方法可以應用於交通、生物學、計算機晶片設計以及其他許多領域的問題。因此，開發處理圖的演算法是計算機科學中的一個重要領域。在那裡，圖的轉換通常被形式化並透過圖重寫系統來表示。它們要麼被直接使用，要麼研究重寫系統的屬性（例如匯合）。作為側重於基於規則的圖記憶體操作的圖轉換系統，圖資料庫側重於對圖結構化資料的交易安全、持久儲存和查詢。

圖論方法以各種形式在語言學中已被證明特別有用，因為自然語言通常非常適合離散結構。傳統上，句法和組合語義遵循基於樹的結構，其表達能力在於組合原理，在分層圖中建模。在詞彙語義中，特別是應用於計算機時，當在相關詞語的意義上理解給定詞語時，對詞語意義進行建模更容易；因此，語義網路在計算語言學中很重要。在音系學（例如，最優性理論，使用格圖）和形態學（例如，有限狀態形態學，使用有限狀態轉換器）中，還有其他方法在將語言分析為圖時很常見。事實上，這個數學領域對語言學的用處已經產生了像TextGraphs這樣的組織，以及各種“Net”專案，如WordNet、VerbNet等等。

圖論也被用於研究化學和物理學中的分子。在凝聚態物理學中，可以透過收集與原子拓撲結構相關的圖論屬性的統計資訊來定量研究複雜模擬原子結構的三維結構。例如，Franzblau 的最短路徑 (SP) 環。在化學中，圖對分子構成一個自然的模型，其中頂點代表原子，邊代表鍵。這種方法特別用於分子結構的計算機處理，從化學編輯器到資料庫搜尋。在統計物理學中，圖可以表示相互作用系統各個部分之間的區域性連線，以及這些系統上物理過程的動力學。

圖論在社會學中也得到了廣泛應用，例如，用它來衡量演員的聲望或探索w:擴散機制，特別是透過使用w:社會網路分析軟體。

同樣，圖論在w:生物學和保護工作中也很有用，其中頂點可以代表某些物種存在（或棲息地）的區域，邊代表遷徙路徑或區域之間的移動。當檢視繁殖模式或跟蹤疾病、寄生蟲的傳播或運動變化如何影響其他物種時，這些資訊非常重要。

在數學中，圖在幾何學和拓撲學的某些部分很有用，例如紐結理論。代數圖論與群論有著密切的聯絡。

可以透過為圖的每條邊分配一個權重來擴充套件圖結構。帶有權重的圖，或w:帶權圖，用於表示成對連線具有某些數值的結構。例如，如果圖表示一個道路網路，權重可以代表每條道路的長度。

在圖論中，帶有加權邊的有向圖被稱為網路。網路分析具有許多實際應用，例如，對交通網路進行建模和分析。網路分析的應用大體分為三類

首先，分析以確定網路的結構屬性，例如頂點度數的分佈和圖的直徑。存在大量圖度量，針對不同領域產生有用的度量仍然是研究的活躍領域。
其次，分析以在網路中找到可衡量的量，例如，對於交通網路，任何部分的車輛流量水平。
第三，分析網路的動力學屬性。

歷史

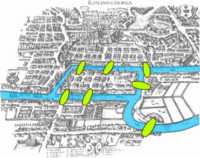
萊昂哈德·尤拉關於w:哥尼斯堡七橋問題的論文寫於 1736 年，被認為是圖論歷史上第一篇論文。^[1] 這篇論文以及範德蒙德關於騎士巡遊問題的論文，延續了萊布尼茨發起的位相分析。尤拉關於凸多面體的邊數、頂點數和麵數之間的關係的公式由柯西^[2]和L'Huillier^[3]研究和推廣，是w:拓撲學的起源。

尤拉關於 w:柯尼斯堡橋樑的論文發表一個多世紀後，雖然李斯廷引入了拓撲學，但凱萊從 w:微積分中出現的特定解析形式的研究中，開始研究一類特定的圖，即樹。這項研究對理論 w:化學產生了諸多影響。所涉及的技術主要與 w:圖的列舉具有特定性質的圖有關。列舉圖論由此起源於凱萊的研究成果，以及波利亞在 1935 年至 1937 年間發表的基礎成果，以及德布魯因在 1959 年對這些成果的推廣。凱萊將他在樹方面的成果與當時對化學成分的研究聯絡起來。^[4] 數學思想與化學思想的融合是圖論標準術語的一部分的起源。

特別是，“圖”這個詞是由西爾維斯特在 1878 年發表在自然上的一篇論文中提出的，他在論文中將代數的“量子不變數”和“共變數”與分子圖進行了類比:^[5]

“[...] 因此，每個不變數和共變數都可以用一個圖來表示，該圖與凱庫勒圖或化學圖完全相同。[...] 我給出圖形幾何乘法的規則，即，如何為已知單獨圖形的不變數或共變數的乘積構造一個圖形。[...]”（斜體與原文一致）。

圖論中最著名、最有成效的問題之一是 w:四色問題：“是否真的任何繪製在平面上的地圖都可以用四種顏色對它的區域進行著色，使得任何兩個具有共同邊界的區域都具有不同的顏色？”這個問題最早是由 w:弗朗西斯·格思裡於 1852 年提出的，其第一個書面記錄是在德·摩根寫給哈密爾頓的信中，時間為同年。許多不正確的證明被提出，包括凱萊、肯普以及其他人的證明。對這個問題的研究和推廣，由泰特、希伍德、拉姆齊和哈德維格完成，這導致了對嵌入在具有任意虧格的曲面上的圖的著色的研究。泰特的重新表述產生了一類新的問題，即分解問題，這些問題由彼得森和柯尼格研究。拉姆齊關於著色的研究，更具體地說，圖蘭在 1941 年取得的成果是圖論另一個分支的起源，即w:極圖論。

四色問題在一個多世紀的時間裡一直沒有得到解決。1969 年，w:海因裡希·希施發表了一種使用計算機解決該問題的方法。^[6] 1976 年，w:肯尼斯·阿佩爾和 w:沃爾夫岡·哈肯給出了一個計算機輔助證明，該證明利用了希施提出的“放電”的概念。^[7]^[8] 該證明涉及透過計算機檢查 1,936 種配置的屬性，並且由於其複雜性，當時並沒有完全被接受。20 年後，羅伯遜、西摩、桑德斯和托馬斯給出了一個更簡單的證明，該證明只考慮了 633 種配置。^[9]

拓撲學從 1860 年到 1930 年的自主發展，透過若爾當、庫拉托夫斯基和惠特尼的作品，使圖論重新煥發活力。圖論和拓撲學共同發展另一個重要因素來自於現代代數技術的應用。第一個此類應用的例子來自物理學家 w:古斯塔夫·基爾霍夫的工作，他在 1845 年發表了計算 w:電路中 w:電壓和電流的 w:基爾霍夫電路定律。

在圖論中，特別是埃爾德什和雷尼關於圖連通性的漸進機率的研究中引入了機率方法，這催生了另一個分支，稱為隨機圖論，它一直是圖論結果的一個富有成效的來源。

繪製圖形

透過為每個頂點繪製一個點或圓圈，並在兩個頂點之間繪製一條弧線（如果它們由一條邊連線）來圖形地表示圖。如果圖是有向的，則透過繪製箭頭來指示方向。

不應將圖的繪製與圖本身（抽象的、非視覺結構）混淆，因為圖的繪製有多種方式。重要的是哪些頂點透過多少條邊連線到哪些其他頂點，而不是確切的佈局。實際上，很難決定兩個圖是否代表同一個圖。根據問題域，一些佈局可能比其他佈局更適合，更容易理解。

圖論資料結構

在計算機系統中儲存圖的方法有很多。使用的 w:資料結構取決於圖的結構以及用於操作圖的 w:演算法。從理論上講，可以區分列表結構和矩陣結構，但在具體應用中，最佳結構通常是兩者的組合。列表結構通常更適合 w:稀疏圖，因為它們具有較小的記憶體需求。另一方面，矩陣結構為某些應用程式提供了更快的訪問速度，但可能會消耗大量記憶體。

列表結構

w:關聯列表: 邊用一個包含頂點對（如果是帶方向的，則為 w:元組）的陣列來表示（邊連線的頂點），並可能包含權重和其他資料。由一條邊連線的頂點被稱為相鄰的。
w:鄰接列表: 與關聯列表非常相似，每個頂點都有一個列表，列出它與哪些頂點相鄰。這會在無向圖中導致冗餘：例如，如果頂點 A 和 B 相鄰，則 A 的鄰接列表包含 B，而 B 的列表包含 A。鄰接查詢速度更快，但需要額外的儲存空間。

矩陣結構

w:關聯矩陣: 圖用一個大小為 |V |（頂點數）乘以 |E|（邊數）的矩陣來表示，其中條目 [頂點，邊] 包含邊的端點資料（最簡單的情況：1 - 相鄰，0 - 不相鄰）。
w:鄰接矩陣: 這是一個n 乘以n 的矩陣A，其中n 是圖中頂點的數量。如果從頂點x 到頂點y 有一條邊，則元素 $a_{x,y}$ 為 1（或者更一般地，為xy 邊數），否則為 0。在計算中，這個矩陣使得很容易找到子圖，以及反轉有向圖。
w:拉普拉斯矩陣或 w:基爾霍夫矩陣或導納矩陣: 它被定義為 D − A，其中 D 是對角線 w:度矩陣。它顯式地包含鄰接資訊和度資訊。（然而，還有其他類似的矩陣也稱為圖的“拉普拉斯矩陣”。）
w:距離矩陣: 一個對稱的 n 乘 n 矩陣 D，它的元素 $d_{x,y}$ 是 x 和 y 之間 w:最短路徑的長度；如果不存在這樣的路徑，則 $d_{x,y}$ = 無窮大。它可以從 A 的冪推匯出。; $d_{x,y}=\min\{n\mid A^{n}[x,y]\neq 0\}.\,$

圖論中的問題

列舉

關於 w:圖形列舉存在大量的文獻：計數滿足指定條件的圖形的問題。其中一些工作可以在 Harary 和 Palmer（1973）中找到。

子圖、匯出子圖和次圖

一個常見的問題，稱為 w:子圖同構問題，是在給定圖中找到一個固定圖作為 w:子圖。對這個問題感興趣的原因之一是，許多 w:圖屬性對於子圖是 遺傳的，這意味著一個圖具有該屬性當且僅當它的所有子圖也具有該屬性。不幸的是，找到某種型別的最大子圖通常是一個 w:NP 完全問題。

找到最大的 w:完全圖被稱為 w:團問題（NP 完全）。

一個類似的問題是找到給定圖中的 w:匯出子圖。同樣地，一些重要的圖屬性對於匯出子圖是遺傳的，這意味著一個圖具有該屬性當且僅當它的所有匯出子圖也具有該屬性。找到某種型別的最大匯出子圖也通常是 NP 完全的。例如，

找到最大的無邊匯出子圖，或獨立集，被稱為 w:獨立集問題（NP 完全）。

另一個類似的問題，即 次圖包含問題，是在給定圖中找到一個固定圖作為次圖。一個圖的次圖或 子收縮圖 是透過取一個子圖並收縮一些（或沒有）邊而獲得的任何圖。許多圖屬性對於次圖是遺傳的，這意味著一個圖具有該屬性當且僅當它的所有次圖也具有該屬性。一個著名的例子

一個圖是平面圖，如果它不包含 w:完全二部圖 $K_{3,3}$ （參見 w:三間小屋問題）或完全圖 $K_{5}$ 作為次圖。

另一類問題與各種物種和圖的推廣在多大程度上由它們的 點刪除子圖 決定有關，例如

The w:重建猜想

圖著色

許多問題與圖著色的各種方法有關，例如

The w:四色定理
The 強完美圖定理
The w:Erdős–Faber–Lovász 猜想（未解決）
The 總著色猜想（未解決）
The 列表邊著色猜想（未解決）
The w:Hadwiger 猜想（圖論）（未解決）

路線問題

網路流

許多問題特別是來自與網路流的各種概念相關的應用，例如

w:最大流最小割定理

可見性圖問題

w:博物館守衛問題

覆蓋問題

覆蓋問題是子圖查詢問題的一些特定例項，它們往往與 w:團問題或 w:獨立集問題緊密相關。

圖類

許多問題涉及到對各種圖類的成員進行特徵化。這種型別的問題與本列表中的其他型別有很大的重疊，例如

列舉一個類的成員
根據禁止子結構來刻畫一個類
確定類之間的關係（例如，一個圖的屬性是否意味著另一個屬性）
找到有效的 w:演算法來判定對一個類的成員關係
為一個類的成員找到表示

另請參閱

演算法

子領域

數學相關領域

概括

傑出圖論學家

註釋

↑ Biggs, N.; Lloyd, E. 和 Wilson, R. (1986), 圖論，1736-1936, 牛津大學出版社{{citation}}: CS1 maint: multiple names: 作者列表 (link)
↑ Cauchy, A.L. (1813), "關於多面體的研究 - 第一篇論文", 理工學院雜誌, 9 (Cahier 16): 66–86.
↑ L'Huillier, S.-A.-J. (1861), "關於多面體的論文", 數學年鑑, 3: 169–189.
↑ Cayley, A. (1875), "關於在數學中被稱為樹的解析圖形及其在化學鍵理論中的應用", 德國化學學會通訊, 8: 1056–1059, doi:10.1002/cber.18750080252.
↑ John Joseph Sylvester (1878), 化學與代數. 自然，第 17 卷，第 284 頁。 doi:10.1038/017284a0. 線上版本. 2009-12-30 檢索.
↑ Heinrich Heesch: 關於四色問題的研究. 曼海姆: 文獻研究所 1969.
↑ Appel, K. 和 Haken, W. (1977), "每個平面地圖都是四色的。第一部分。放電", 伊利諾伊州數學雜誌, 21: 429–490.{{citation}}: CS1 maint: 多個名稱: 作者列表 (link)
↑ Appel, K. 和 Haken, W. (1977), “每張平面圖都是四色的。第二部分：可約性”，伊利諾伊州數學雜誌，21: 491–567。{{citation}}: CS1 maint: 多個名字：作者列表 (link)
↑ Robertson, N.；Sanders, D.；Seymour, P. 和 Thomas, R. (1997), “四色定理”，組合理論雜誌 B 系列，70: 2–44，doi:10.1006/jctb.1997.1750.{{citation}}: CS1 maint: 多個名字：作者列表 (link)

參考文獻

Berge, Claude (1958), 圖論及其應用，大學數學叢書，卷。 II，巴黎：Dunod。英語版，Wiley 1961 年；Methuen & Co，紐約 1962 年；俄語，莫斯科 1961 年；西班牙語，墨西哥 1962 年；羅馬尼亞語，布加勒斯特 1969 年；中文，上海 1963 年；1962 年第一版英語版的第二次印刷，Dover，紐約 2001 年。
Biggs, N.；Lloyd, E.；Wilson, R. (1986), 圖論，1736–1936，牛津大學出版社.
Bondy, J.A.；Murty, U.S.R. (2008), 圖論，施普林格，ISBN 978-1-84628-969-9.
Chartrand, Gary (1985), 圖論導論，Dover，ISBN 0-486-24775-9.
Gibbons, Alan (1985), 演算法圖論，劍橋大學出版社.
Golumbic, Martin (1980), 演算法圖論與完美圖，學術出版社.
Harary, Frank (1969), 圖論，馬薩諸塞州雷丁：Addison-Wesley.
Harary, Frank；Palmer, Edgar M. (1973), 圖形列舉，紐約，紐約：學術出版社.
Mahadev, N.V.R.；Peled, Uri N. (1995), 閾值圖及相關主題，北荷蘭.

外部連結

線上教科書

圖論及其應用 (1976) 作者：Bondy 和 Murty
組合最佳化問題中的相變，第 3 節：圖論導論 (2006) 作者：Hartmann 和 Weigt
有向圖：理論演算法及應用 2007 作者：Jorgen Bang-Jensen 和 Gregory Gutin
圖論，作者：Reinhard Diestel

其他資源

[Biggs-1] Biggs, N.; Lloyd, E. 和 Wilson, R. (1986), 圖論，1736-1936, 牛津大學出版社{{citation}}: CS1 maint: multiple names: 作者列表 (link)

[Cauchy-2] Cauchy, A.L. (1813), "關於多面體的研究 - 第一篇論文", 理工學院雜誌, 9 (Cahier 16): 66–86.

[Lhuillier-3] L'Huillier, S.-A.-J. (1861), "關於多面體的論文", 數學年鑑, 3: 169–189.

[Cayley1-4] Cayley, A. (1875), "關於在數學中被稱為樹的解析圖形及其在化學鍵理論中的應用", 德國化學學會通訊, 8: 1056–1059, doi:10.1002/cber.18750080252.

[Sylvester-5] John Joseph Sylvester (1878), 化學與代數. 自然，第 17 卷，第 284 頁。 doi:10.1038/017284a0. 線上版本. 2009-12-30 檢索.

[6] Heinrich Heesch: 關於四色問題的研究. 曼海姆: 文獻研究所 1969.

[AA1-7] Appel, K. 和 Haken, W. (1977), "每個平面地圖都是四色的。第一部分。放電", 伊利諾伊州數學雜誌, 21: 429–490.{{citation}}: CS1 maint: 多個名稱: 作者列表 (link)

[AA2-8] Appel, K. 和 Haken, W. (1977), “每張平面圖都是四色的。第二部分：可約性”，伊利諾伊州數學雜誌，21: 491–567。{{citation}}: CS1 maint: 多個名字：作者列表 (link)

[RSST-9] Robertson, N.；Sanders, D.；Seymour, P. 和 Thomas, R. (1997), “四色定理”，組合理論雜誌 B 系列，70: 2–44，doi:10.1006/jctb.1997.1750.{{citation}}: CS1 maint: 多個名字：作者列表 (link)

[4]

[5]

[6]

[7]

[8]

[9]

應用

歷史