交通地理與網路科學/網路增長模型

背景

克里斯塔勒（1933）根據交通的經濟原理考察了中心地的形成，他指出，“人口的需求、運輸成本、投資資本的成本等等，決定性地影響著交通系統的形成”。交通網路和土地利用是城市形態相互依存的塑造者。首先，土地利用的變化改變了出行需求模式。其次，交通流量的增加促使官員透過擴大交通設施來做出回應。第三，新的交通設施改變了可達性模式，這推動了活動的選址和出行行為。

生命週期模型

生命週期模型預測了特定時間點上技術部署的份額。

${\frac {f}{1-f}}=e^{at+b}$

其中： $f$ = 技術的份額（技術在最終市場份額中的份額） $t$ = 時間 $a,b$ = 模型引數

關於交通網路增長的文獻並不多。一些研究人員考慮了對網路結構進行建模的問題。Taaffe 等人（1963）研究了道路如何在發展中國家從港口出現，Garrison 和 Marble（1965）考慮了愛爾蘭鐵路中連結的建設順序，Helbing 等人（1997）採用了 Lam 和 Pochy（1993）的主動步行者模型，允許在景觀上移動的步行者改變景觀，Watts 和 Strogatz（1998）提出了小世界模型，Barabasi 等人（1999a，b）建議偏好連線，以便已經連線的節點獲得更多連線，這解釋了樞紐，而 Yamins 等人（2003）將道路與城市聚落共同進化。

經驗模型

還進行了一系列研究，估計現有交通設施擴充套件和新建連結建設的經驗模型（Levinson 和 Karamalaputi 2003a，b）。

基於代理的模型

幾篇論文開發了基於代理的模型（使用連結代理）來處理具有固定或隨機土地利用模式的網路元素的組織、增長和收縮（Yerra 和 Levinson 2004，Levinson 和 Yerra 2005）。這些模型在一系列論文中得到了擴充套件（收集在 Xie 和 Levinson 2011 中），放寬了固定網路拓撲、完全分散的代理和缺乏擁堵的假設。

網路增長系統 (SONG) 模型

SONG 模型可以在 [1] 訪問。

概述

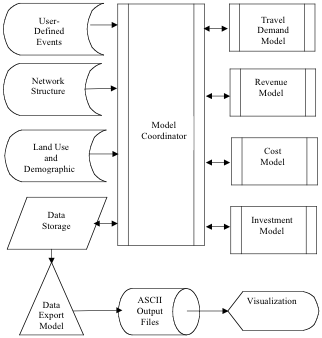
網路增長系統 (SONG) 模型的組成部分包括出行需求、收益、成本和投資。出行需求模型使用給定的網路拓撲將人口和就業資料轉換為交通流量，並透過遵循傳統的規劃步驟（出行產生、出行分配和交通分配）來確定連結流量（為簡化起見，假設單一模式）。收益模型根據連結的速度、流量和長度來確定交通流量使用道路必須支付的價格。在下面的實驗中，連結長度是固定的，因此收益與連結長度無關，但是，與模型中的所有假設一樣，這個假設也可以放寬。成本模型根據交通流量計算維持連結速度所需的成本。超過維護成本的收益將根據投資模型投資於連結以改善其狀況，直到所有收益都被消耗掉。在升級（或降級）網路中的每個連結後，時間段會遞增，整個過程會重複，直到達到平衡，或者很明顯無法實現平衡。圖 1 顯示了這些模型的概述和相互連線。

複雜系統由許多自治代理組成，它們的相互作用導致系統屬性不同於代理屬性（單個連結的速度無法告訴你道路的存在，一條道路本身並不表明道路等級（有不同的高速公路、訊號燈化的主幹道、本地街道）的存在。等級描述了特定網路元素與同一型別其他元素的規模。將交通網路建模為複雜系統涉及對節點（充當交叉路口以及傳統出行需求文獻中被認為是交通區域中心的節點）、連結（路段）、土地利用單元以及旅行者屬性及其相互作用進行建模。在 SONG 中，網路拓撲被視為既定因素，連結和系統屬性被建模為替代輸入的函式。

SONG 將網路演變建模為自下而上的過程，而不是自上而下的過程。規劃者和工程師會爭辯說，交通網路投資是現在由中央組織（例如州交通部或都市規劃組織）驅動的或協調的決策，這些組織使用預測模型和規劃流程來測試和評估替代方案，從而做出重大投資決策。地方管轄區（在一些都市區有很多）對較低級別的道路進行投資。當然，這些組織確實會影響新的投資，但建設或擴充套件連結的決定也受到許多實際情況的制約，例如連結上的實際交通量、競爭的平行連結以及互補的、上游和下游連結、擴充套件成本以及有限的預算。如果我們能夠在沒有任何集中規劃或指導的情況下生成對網路結構令人信服的表示，那麼規劃在塑造城市區域方面可能並不像人們有時認為的那樣重要，而是相對簡單地遵循需求。

這裡的示例使用網格網路結構出於以下幾個原因。首先，展示的示例測試了替代土地利用模式；同時改變網路拓撲和土地利用會使關於影響的結論變得更加困難。其次，網格是一種廣泛使用的拓撲，可以在美國的大多數地方找到（尤其是中西部和西部，因為 1785 年的土地法令建立了公共土地測量系統），網格的基本結構是在確定更詳細的因素（如街道寬度（以及它們的重要性））之前就已經確定的。以及相關的土地利用。第三，網格不僅限於美國，它已在各種地方以各種形式使用，其中包括埃及的吉薩、印度河流域的摩亨佐·達羅、漢謨拉比時代的巴比倫、中國和其他亞洲國家的各種首都城市、由希波達摩斯設計的希臘城市（如米利都）、大多數羅馬城市規劃、墨西哥的特奧蒂瓦坎以及整個美洲的西班牙殖民地。當然，也可以測試其他網路拓撲（或拓撲的缺失），留給學生作為練習。

土地利用和出行產生

土地利用被建模為稱為土地利用單元的土地塊的網格排列。每個土地利用單元儲存其位置、人口密度和市場密度（零售和辦公空間的聚合）。使用這些資料，出行產生模型計算從每個土地利用單元吸引和產生的出行。為了簡化分析，假設從土地利用單元產生的出行與人口密度成正比，而吸引到土地利用單元的出行與市場密度成正比。因此，土地利用單元所持有的資訊可以被視為產生的出行。

令 $(x',y')$ 為表示土地利用單元位置的有序對，其中 $x'$ 是單元在 x 方向上的位置， $y'$ 是單元在 y 方向上的位置。令 $X$ 和 $Y$ 分別表示在 $x$ 和 $y$ 方向上的土地利用單元總數。令 $p(x',y')$ 和 $q(x',y')$ 分別是土地利用單元 $(x',y')$ 產生的出行和吸引的出行。由於地理區域中產生的出行總數等於吸引的出行總數，因此以下等式始終成立。

$\sum \limits _{({x}',{y}')}^{(X,Y)}{p({x}',{y}')=\sum \limits _{({x}',{y}')}^{(X,Y)}{q({x}',{y}')}}$

每個土地利用單元被分配到最近的網路節點。土地利用單元與其最近網路節點之間的通勤成本被忽略。透過將分配到該網路節點的所有土地利用單元的出行量加起來，計算網路節點產生的總出行量和吸引的總出行量。令 ${O_{n}}$ 表示所有距離網路節點 $n$ 比其他任何網路節點更近的土地利用單元集合。透過比較土地利用單元與其周圍網路節點之間的距離，將最近的網路節點分配給土地利用單元。每個網路節點的出行量就是分配給它的所有單元的出行量的總和。

$p_{r}=\sum \limits _{\forall ({x}',{y}')\in \{O_{r}\}}{p({x}',{y}')}$

$q_{s}=\sum \limits _{\forall ({x}',{y}')\in \{O_{s}\}}{q({x}',{y}')}$

其中，

$p_{r}$ 是從網路節點 $r$ 產生的（發起的）出行量，

$q_{s}$ 是吸引到（目的地為）網路節點 $s$ 的出行量。

網路層

任何網路都可以被視為由連線在一起的節點（或頂點）和連結（或邊或弧）組成的集合。此處的交通網路是有向圖 ${G}$ 。令 ${N}$ 表示按順序編號的節點，並令 ${A}$ 表示按順序編號的有向連結，連線 ${N}$ 中的節點。令 $N$ 表示集合 ${N}$ 中的元素數量（節點數量），而 $A$ 表示集合 ${A}$ 中的元素數量（連結（或弧）數量）。令 ${R}$ 表示一組起點節點，而 ${S}$ 表示一組終點節點。請注意，在本文建模的網路中， ${R}={S}={N}$ ，即每個節點都充當起點和終點。從起點節點 $r$ 連線到終點節點 $s$ 的連結 $a$ 表示為 $r\rightarrow s$ 。

令 $x_{n}$ 和 $y_{n}$ 表示節點 $n\in {N}$ 在笛卡爾座標系中的 $x$ 和 $y$ 座標。令 $l_{a}$ 為邊 $a$ 的長度。那麼 $x_{n}$ 和 $y_{n}$ 是節點 $n$ 的靜態變數，而 $l_{a}$ 是邊 $a$ 的靜態屬性。令 $v_{at}$ 為時間步長 $t$ 時，邊 $a\in {A}$ 上車輛的平均速度，稱為邊速度。邊上的行駛時間，即邊長與邊速度之比，是流量的阻抗。假設網路節點沒有流量阻抗。由於圖中的邊是有方向的——例如，從節點 1 到節點 2 的邊不同於從節點 2 到節點 1 的邊——因此我們得到一個有向圖。

出行分配模型

出行分配將從一個起點產生的出行分配到一個目的地，形成一個起點-目的地矩陣（OD 矩陣），其中行表示每個區域的出行起點總數，列表示每個區域的出行目的地總數。

令 $m_{rst}$ 為時間步長 $t$ 時，從網路節點 $r$ 出發，到達網路節點 $s$ 的出行數量。那麼，以下關係在每個時間步長 $t$ 都成立。

$p_{r}=\sum \limits _{s=1}^{N}{m_{rst}^{}}\forall r\in \{N\}$

$q_{s}=\sum \limits _{r=1}^{N}{m_{rst}^{}}\forall s\in \{N\}$

本研究採用單約束重力模型 (Hutchinson, 1974)。每個 OD 對的出行量為

$m_{rst}^{}=p_{r}{\frac {q_{s}\cdot h(d_{rst}^{})}{\sum \limits _{s}{q_{s}\cdot h(d_{rst}^{})}}}\forall r,s\in \{N\}$

其中，採用負指數模型

$h(d_{rs})=e^{-w\cdot d_{rs}}$

使得

$d_{rst}^{}=\sum \limits _{a\in A}{d_{at}^{}}\delta _{a,rst}^{}\forall r,s\in \{N\}$

其中： $\delta _{a,rst}$ 是虛擬變數，如果連結 $a$ 屬於 $r$ 和 $s$ 之間的最短路徑，則為 1，否則為 0。

$d_{at}$ 是在弧 $a$ 上出行的廣義成本。

$d_{rst}$ 是在節點 $r$ 和 $s$ 之間出行的廣義成本。

為了定義任何兩個節點之間出行的廣義成本，有必要定義在連結上出行的廣義成本。在時間步長 $t$ 上，在連結 $a$ 上出行的廣義成本假設由兩部分組成：轉換為貨幣價值的出行時間和通行費，通行費允許根據連結長度和速度變化。

$d_{at}^{}={\frac {l_{a}}{v_{at}^{}}}+\rho _{0}(l_{a})^{\rho _{1}}(v_{a}^{t})^{\rho _{3}}$

其中

$d_{a}t$ 是弧 $a$ 上的通勤泛化成本

$\rho _{0}$ 是基本通行費（使用單位長度和速度的連線的固定成本）

$\rho _{1}$ 是一個係數，代表連線長度的定價結構：通行費相對於長度的彈性

$\rho _{3}$ 是一個係數，代表連線速度的定價結構：通行費相對於速度的彈性

路線分配

使用 OD 矩陣和使用 Dijkstra 演算法（Chachra 等人，1979）計算的最短路徑資訊，可以透過將經過該連線的任何起點和終點的行程進行求和來計算每個連線上的流量。

$f_{at}^{}=\sum \limits _{rs}{m_{rst}^{}\delta _{a,rst}^{}\forall a\in A}$

其中， $f_{at}$ 是時間步長 $t$ 中連線 $a$ 上的交通流量。

收益模型

收益模型估計收取的收益，其中收益僅僅是通行費和流量的乘積。通行費本身是一個泛化函式，如上式 $d_{at}$ 中所述，它隨長度和速度而變化。收益 ( $E_{at}$ ) 是第 $t$ 年每個連線可用的資金。

$E_{at}^{}=(\rho _{0}\cdot (l_{a})^{\rho _{1}}(v_{a}^{t})^{\rho _{3}})\cdot (\psi \cdot f_{at}^{})\forall a\in A$

其中： $\psi$ 是將流量年化的模型引數。

成本模型

在經驗模型中，通常發現高速公路維護和擴建的成本可以用科布-道格拉斯形式很好地表示（例如 Levinson 和 Gillen 1998 以及 Levinson 和 Yerra 2002，他們都發現科布-道格拉斯模型比其他函式形式更適合）。成本通常是產出（例如，按車輛型別劃分的流量）、網路規模、價格和質量指標的函式。該模型不考慮價格（假設價格是外生的，並且隨著時間的推移是固定的（或以與收入相同的速率上升）），但考慮了其他三個變數。維護連結 $(C_{at})$ 在某一年中的成本由下式給出：

$C_{at}^{}=\mu \cdot (l_{a})^{\alpha _{1}}(f_{at}^{})^{\alpha _{2}}(v_{at}^{})^{\alpha _{3}}f_{at}^{}\forall a\in A$

其中

$\mu$ 是（年度）連結維護的單位成本。

$\alpha _{1},\alpha _{2},\alpha _{3}$ 是表示關於長度、流量、速度的規模經濟或規模不經濟的係數。

投資模型

在提出的投資模型中，如果一個連結代理人在某一年中存在超額收益（超出維持連結當前速度所需的收益），它可以使用該收益來改善連結（使其更快）。如果一個連結出現赤字，它就無法負擔全部維護費用，連結速度就會下降。反映這一點的方程由下式給出：

$v_{at+1}^{}=v_{at}^{}\left({\frac {E_{at}^{}}{C_{at}^{}}}\right)\forall a\in A$

在文獻中，迄今為止還沒有經驗投資模型可供參考，因此該函式具有一定的隨意性。必須承認，投資模型很簡單且短視，我們認為，如果它能夠再現被認為是由更復雜過程產生的結果，那麼這將是該模型的優勢。未來的研究可以測試替代的投資模型，包括使用政府或銀行等中央代理人來重新分配超額資金的投資，或者即使連結無利可圖，也要確保提供基本的服務水平。

應用平均規則以確保連結及其反向連結共享相同的設計，這是道路的典型特徵。

$v_{at+1}^{}=v_{{a}'t+1}^{}={\frac {v_{at+1}^{}+v_{{a}'t+1}^{}}{2}}$

如果從交通分配模型中應用對稱條件，則不需要應用此條件，因為這些對稱條件會自動確保 $a$ 和 $a'$ 具有相同的流量。

實驗

考慮了三種土地利用模式：隨機、均勻和鐘形。以下各小節將詳細介紹每個類別。

隨機分佈的土地利用

土地使用屬性（如人口和就業）的空間分佈取決於許多因素，其中一些變數是相互依存的。在隨機分佈的土地使用中，每個土地使用單元格產生的出行量和吸引的出行量在整個地理區域內都是隨機分佈的。產生的和吸引的出行量分佈在給定的最小值和最大值之間。

$p({x}',{y}'),q({x}',{y}'){\tilde {\ }}Un(u_{\min },u_{\max })$

統一土地使用

可以透過使用方程式 (14) 中所示的分佈來分配統一的土地使用模式，其中每個單元格在整個地理區域中都具有相同的屬性，使用相同的 $u_{min}$ 和 $u_{max}$ 值。這種土地使用模式是控制土地使用對道路等級形成影響所必需的。

鐘形土地使用

實際上，土地使用的分佈並不完全隨機。在具有中央商務區的城市地區，土地使用變數的分佈通常可以表示為鐘形或倒鐘形的曲面。在這種情況下，吸引的出行量 $q(x',y')$ 被建模為沿半徑接近地理區域中心時增加。產生的出行量與住宅密度成正比，假設在中心處最小，類似於倒鐘形的曲面。圖 2 顯示了沿半徑方向假設的產生的出行量和吸引的出行量分佈的橫截面的示意圖。吸引的出行量空間分佈函式如方程式所示

$q({x}',{y}')=u_{\min }+(u_{\max }-u_{\min })e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}$

其中， $d_{x})$ 是市中心沿 x 軸土地使用單元格的位置，

$d_{y}$ 是市中心沿 y 軸土地使用單元格的位置， $z)$ 是一個取決於市中心範圍的因素。

將上述方程式中的 $q(x',y')$ 代入初始方程式，得到

$\sum \limits _{({x}',{y}')}^{(X,Y)}{p({x}',{y}')}=\sum \limits _{({x}',{y}')}^{(X,Y)}{q({x}',{y}')}=X\cdot Y\cdot u_{\min }+(u_{\max }-u_{\min })\sum \limits _{({x}',{y}')}^{(X,Y)}{e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}}$

假設出行產生的表面呈倒置鐘形，則 $p(x',y')$ 的分佈是使用以下公式計算的

$p({x}',{y}')=u^{*}-(u_{\max }-u_{\min })e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}$

其中，

$u^{*}=u_{\min }+{\frac {2(u_{\max }-u_{\min })}{X\cdot Y}}\sum \limits _{({x}',{y}')}^{(X,Y)}{e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}}$

模型引數

表 1 給出了模型中引數的值。這些引數在註明的情況下已被固定，以便在本次研究中對感興趣的變數（土地利用模式）進行可比性分析。初始速度被賦予單位值，土地利用（每個單元格產生的和吸引的出行次數）在基本情景中為 10 個單位。土地利用實驗中的出行分配模型係數 ( $w$ ) 為 0.01，除非另有說明；較高的係數意味著旅行者對旅行成本更加敏感，因此會進行更短的旅行，這些情況將在單獨的測試中進行測試。通行費設定為與路線長度線性增長，並且不受道路質量（速度）的影響。收入和成本系數被縮放以假設 365 天中的每一天都是相等的，以使價值年化（這顯然是一種理想化，忽略了例如週末）。成本隨長度線性增長。然而，存在規模經濟，因此流量增長 1%，成本僅增長 0.75%。同樣，當速度增長 1% 時，成本僅增長 0.75%。這種規模經濟的一般假設得到了文獻的支援，儘管確切的幅度存在爭議。Small、Winston 和 Evans（1989）報告了與路面厚度相關的顯著規模經濟，這體現了其承載負荷的能力。他們還發現，在提供道路容量方面存在輕微的規模經濟；即承載交通的能力。Yerra 和 Levinson（2002）也報告了汽車和卡車的規模經濟。為了能夠探索感興趣的變數，這些引數再次被固定。

變數	描述	'	基本假設

$v_{a0}$	初始速度（整數）	1
$g_{z},h_{z}$	網格 z 的土地利用屬性	10
$w$	出行分配模型中的係數（土地利用實驗）	0.01
$\rho _{0}$	收益模型中的係數	1.0
$\rho _{1}$	收益模型中的長度冪	1.0
$\rho _{3}$	收益模型中的速度冪	0.0
$\tau$	收益模型中的稅率	1.0
$\psi$	收益模型引數	365
$\mu$ μ	成本模型中的單位成本	365
$\alpha _{1}$	成本模型中的長度冪	1.0
$\alpha _{2}$	成本模型中的流量冪	0.75
$\alpha _{3}$	成本模型中的速度冪	0.75

結果

土地利用實驗

基本案例：初始速度和土地利用均勻分佈 (U/U) - 初始網路中均勻速度的空間分佈
基本案例：初始速度和土地利用均勻分佈 (U/U) - 網路在經過 8 次迭代後達到平衡時的速度空間分佈。
初始速度均勻分佈，初始土地利用隨機分佈 (U/R) - 實驗 U/R 達到平衡後的速度空間分佈
初始速度隨機分佈，初始土地利用隨機分佈 (R/R) - 實驗 R/R 的初始速度空間分佈（初始速度隨機分佈，初始土地利用隨機分佈）
初始速度隨機分佈，初始土地利用隨機分佈 (R/R) - 網路達到平衡後的速度空間分佈；連線的顏色和粗細表示其相對速度或流量。
初始速度均勻分佈，初始土地利用呈鐘形分佈 (U/B) - 實驗 U/B 的最終速度空間分佈（初始速度均勻分佈，土地利用呈鐘形分佈）

土地利用結果顯示在圖 3-7 中。圖 3 展示了基本案例，初始網路和初始土地利用均勻分佈（表示為 (U/U)）。在基本案例中，一個沒有差異的網路演化成為一個高度差異化的網路，既包含一條主要的南北軸和東西軸，也包含兩條環形道路。其他圖與基本案例相似，都具有層次結構，但有所不同，因為層次結構沒有那麼規則或對稱。這些案例與基本案例的初始狀態相同，但初始速度和土地利用特性的處理方式不同。在土地利用隨機分佈的實驗中，網格的土地利用特性在 10 到 15 次出行之間隨機分佈。在這種情況下，從土地利用網格產生的出行和吸引到該網格的出行不必相同，儘管所有土地利用網格產生的出行總數和吸引的出行總數相同。本模型中的連線速度採用兩種處理方式；首先（實驗 U/R），假設每條連線的速度都相同，大小為 1，與基本案例相同。其次（實驗 R/R），速度在 1 到 5 之間隨機分佈。典型的解決方案如圖 4 和 5 所示。

請注意實驗 U/R 和 R/R 的結果網路的相似性。我們認為土地利用分佈（和速度）以及邊界是造成這種層次結構的原因。

圖 6 (U/B) 和 7 (R/B) 採用了城市鐘形土地利用分佈。城市土地利用分佈使得網路中心與杯形吸引的出行和產生的出行函式的中心重合。由於更多出行被吸引到網路中心，因此自然會期望通往中心的連線承載較高的交通量。請注意圖 6 中 X 和 Y 方向主要道路的均勻間距，以及主要道路都通向網路中心，那裡集中了大部分活動。圖 6 中中心周圍有三個環，而圖 3 中只有兩個主要環。此外，主要的南北軸和東西軸發生分叉，部分交通量被引流到環形道路，而其他交通量則繼續透過中心。圖 7 的初始速度隨機分佈，其模式與圖 4 或 5 相似，中心周圍只有一個不對稱環，儘管它被偏移，因為隨機的初始條件會導致不同的結果網路。空間互動實驗

空間互動引數實驗

重力模型引數變化，網路和土地利用均勻分佈 (U/U) $w=0.02$ (對出行成本不太敏感) 時，平衡狀態下相對速度的空間分佈。
重力模型引數變化，網路和土地利用均勻分佈 (U/U) $w=0.8$ (對出行成本更敏感) 時，平衡狀態下相對速度的空間分佈。
對於 10X10、11X11 和 15X15 網路，平均連線速度隨 w 的變化。

在另一個實驗中，摩擦係數中的係數 ( $w$ ) 表示出行行為，測試了其敏感性並比較了結果。在這些實驗中，網路和土地利用都與基本假設一致，因此這是 (U/U) 的一個變體。如果 w 為零，則出行分配與出行成本無關。w 的較高 (較低) 值代表一個社會，其中較短 (較長) 的出行更頻繁。圖 8 比較了代表更喜歡短途旅行和長途旅行的兩個 w 值的平衡空間速度分佈。正如預期的那樣，較大 $w$ 的速度空間分佈更平坦，具有更多相對高速的連線，而更喜歡長途旅行的社群則更加分層。然而需要注意的是，雖然更喜歡短途旅行的社群擁有更多相對高速的連線，但它們的絕對高速連線並不更多，也就是說，它們的平均連線速度低於更喜歡長途旅行的社群。

圖 9 和 10 顯示了幾個網路大小下平均交通流量和速度相對於係數 w 的變化。正如預期的那樣，隨著 w 的增加，網路上的平均交通流量 (速度) 下降，表明出行距離更長的社會產生更多交通收入，因此會產生更好的交通基礎設施。

結論

本分析測試了三種不同型別的土地利用 (隨機、均勻和鐘形) 對網格網路的影響。每種土地利用都會產生不同的道路等級結果，一些會產生更顯著的環形道路，另一些則會產生更平坦的網路模式。一個改變出行分配 (空間互動) 模型中摩擦係數的實驗表明，該引數對道路的空間分佈影響很大。我們可能會觀察到，在擁堵 (系統的外部性) 成為問題或存在對脆弱連線可靠性的擔憂的情況下，有時擁有更平坦的連線流量等級分佈是有利的。所有這些情景都讓我們得出結論：道路等級是交通網路與使用者相互作用的湧現屬性。這一發現是在非常簡單的收入、成本和投資假設下發生的。道路的湧現表明網路能夠自組織。

自組織網路可以規劃嗎？規劃的難度在於，由於缺乏合適的預測工具，交通網路的長期形態動態一直以來在本質上是不可預測的，並且它們依賴於許多外生的社會、經濟、政治和技術變化。我們觀察到，在許多方面，城市都是自組織的，而關於分形城市 (Batty and Longley 1994) 的最新文獻也支援這一點。與“市場”均衡不同的個人投資決策將塑造市場或網路的未來發展。顯然，城市既是自組織的，也是規劃的。網路也可以做到。本文開發的模型使我們能夠模擬規劃決策和決策規則對網路未來形態的影響。當與土地利用模型相結合時，可以生成城市系統的完整模型，使我們能夠更全面地瞭解導致城市問題（如擁堵和蔓延）的因素。這些工具使我們能夠在模型中探索這些問題以及可能的解決方案，從長遠來看，這應該比在運作的城市進行現實世界實驗更具成本效益，而現實世界實驗通常是不可行的。人們認為，根據類似於本研究中提出的複雜系統原理建模的基於代理的網路動態可能會被證明是有用的。

例如，在現實中，土地利用分佈既不是均勻的，也不是完美的鐘形曲面。它是一個非常崎嶇的地形，具有不連續性，只有某些小區域顯示出趨勢。這裡介紹的方法提供了使用現實土地利用模式 (例如 Zhang and Levinson 2004) 的靈活性，這提供了更多證據來證明模型框架的效用，但缺點是具有多個同時存在的方面，這些方面不像人工網路和土地利用模式那樣容易解開。

面對自組織網路，需要某種機制來消除負面外部性。對旅行者的干預點眾所周知（例如，對出行進行適當的定價），但對建造網路的代理的干預迄今為止一直留給了政治。這些代理使用了一些規則（這裡高度簡化），這些規則導致機構擴充套件連線，這些規則通常是根據有限的標準制定的（例如，當平均日交通量超過 X 且路面狀況不佳時擴充套件）。更好地理解這些規則以及它們如何在一個系統動態框架中隨著時間的推移發揮作用，為我們提供了一種減少與交通相關的負面影響的另一種方式。

如前所述，土地利用與交通網路動態之間的關係至關重要。許多當前的城市問題都是由於擁堵和蔓延造成的，而這些問題是土地利用與出行需求和交通基礎設施供應之間的不平衡的副產品（或解決方案）。雖然本文提出的模型沒有明確考慮網路對土地利用的影響，但人們推測，對這種反饋關係進行建模將有助於規劃交通專案，為管理擁堵和蔓延提供必要的基礎設施。此外，此類模型可以成為城市和交通規劃者的有效工具。大多數傳統的交通規劃模型將土地利用視為一個給定的變數（如本模型中），但透過包含土地利用的動態，可以捕捉到更豐富的交通以及城市動態。

參考文獻

Barabasi A, Albert R 1999 “Emergence of scaling in random networks.” Science 286 509-512
Barabasi A, Albert R, Jeong H 1999 “Scale-free characteristics of random networks: the topology of the world wide web” Physica A 272 173-187
Batty M, Longley P 1994 Fractal Cities (Academic Press, London)
Chachra V, Ghare P, and Moore J 1979 Applications of Graph Theory Algorithms. (North Holland, New York)
Christaller W 1933 Central Places in Southern Germany (Fischer, Jena, Germany) (English translation by Baskin, C (Prentice Hall, London 1966)).
Fujita M, Krugman P, Venables, A 1999. The Spatial Economy: Cities, Regions, and International Trade (MIT Press, Cambridge, MA)
Garrison W, Marble, D 1965 A Prolegomenon to the Forecasting of Transportation Development. United States Army Aviation Material Labs Technical Report (Office of Technical Services, United States Department of Commerce, Washington, DC)
Helbing D, Keltsch J, Molnár P 1997 “Modeling the evolution of human trail systems” Nature 388: 47.
Hutchinson B 1974 Principles of Urban Transportation Systems Planning. (McGraw-Hill, New York)
Lam L, Pochy R 1993 “Active-walker models: growth and form in non-equilibrium systems” Computation simulation 7, 534.
Lam L 1995 “Active walker models for complex systems” Chaos, Solitons and Fractals 6, 267-285.
Levinson, D and Gillen, D 1998, “The Full Cost of Intericty Highway Transportation” Transportation Research part D 3:4 207-223,
Levinson D and Karamalaputi R 2003a “Predicting the construction of new highway links” Journal of Transportation and Statistics 6(2/3) 81–89
Levinson D and Karamalaputi R 2003b, “Induced supply: a model of highway network expansion at the microscopic level” Journal of Transport Economics and Policy, 37(3) 297–318
Levinson, D and Yerra, B. 2002 “Highway Costs and the Efficient Mix of State and Local Funds” Transportation Research Record: Journal of the Transportation Research Board 1812 27-36
Levinson D 和 Yerra B 2005 “地面交通網路的自組織” 交通科學 (即將出版)
Lösch A 1954 地點經濟學 (耶魯大學出版社，紐黑文)
Schweitzer F，Schimansky-Geier L 1994 “雙組分系統中活躍步行者的聚類” 物理學 A 206 359-379
Small, K, Winston, C & Evans, C 1989 公路工程：一項新的高速公路投資政策。華盛頓特區：布魯金斯學會。
Taaffe E，Morrill R，Gould P 1963 “發展中國家的交通擴充套件：比較分析。” 地理評論 53 (4) 503-529
Watts D，Strogatz S 1998 “‘小世界’網路的集體動力學”，自然 393: 440-442。
Yamins D，Rasmussen S，Fogel，D 2003 “城市道路的增長” 網路與空間經濟學 3 69-85
Yerra B，Levinson D 2004 “交通網路中層次結構的出現” 地區科學年鑑 (即將出版)。
Xie, F., Levinson D 2011 演進中的交通網路，施普林格。
Zhang L，Levinson D 2004 “道路興衰模型” 2004 年 3 月麻省理工學院工程系統研討會論文，劍橋，馬薩諸塞州；可從 Levinson，明尼蘇達大學土木工程系，明尼阿波利斯獲得副本