瞭解 Darcs/補丁理論

只針對數學和計算機科學極客

(偶爾會容忍物理學家)

警告，休閒使用者，您將要閱讀的內容不適合膽小者！如果您是日常的 Darcs 使用者，您可能不需要閱讀此頁面上的任何內容。但是，如果您有興趣瞭解 Darcs 的實際工作原理，我們邀請您捲起袖子，並跟隨我們一起進行這次對不斷發展的補丁理論的導覽。請注意，我自己才剛剛開始學習補丁理論和衝突，所以前面可能存在錯誤。

補丁理論是什麼？

Darcs 補丁形式主義是幫助我們瞭解 Darcs 在儲存庫之間交換補丁時應如何表現的底層“數學”。它在 Darcs 引擎中作為用於表示補丁序列的資料結構和等效於形式主義中操作的 Haskell 函式來實現。本節針對兩個受眾：好奇的旁觀者和想要參與 Darcs 核心開發的人員。我的目標是幫助您理解所有這些數學背後的直覺，這樣您就可以儘快瞭解當前的衝突者研究並開始做出貢獻。請注意，我自己才剛剛開始學習補丁理論和衝突者，所以前面可能存在錯誤。

為什麼要用這麼多數學？

集中式和分散式版本控制系統之間的一個區別是，“合併”是我們幾乎一直都在做的事情，因此我們必須確保正確合併。將版本控制問題變成一個數學問題有兩個影響：它讓我們可以將所有無關的實現細節抽象出來，並且它迫使我們確保我們想出的任何技術都是基礎可靠的，即它們在事情變得越來越複雜時不會崩潰。不幸的是，對於那些不經常使用數學的人來說，數學可能很難，因此我們在本手冊中試圖做的是透過使用具體的、圖解的例子讓您逐漸適應數學。

不過要提醒您的是，“正確合併”並不一定意味著在衝突方面有巧妙的行為。我們將首先關注成功的、無衝突的合併，然後繼續討論 Darcs 處理衝突的方法。

上下文、補丁和變更

讓我們從購物開始。Arjan 正在為即將到來的 Darcs 駭客馬拉松製作購物清單。就在我們說話的時候，他的儲存庫包含一個名為s_list的檔案，其內容為

1 apples
2 bananas
3 cookies
4 rice

注意：您看到的數字只是行號，不是檔案內容的一部分

正如我們將在本書的這個和其他的例子中看到的那樣，我們通常需要給儲存庫的狀態分配一個名稱。我們稱這個名稱為上下文。例如，我們可以說 Arjan 的儲存庫是一個上下文 $o$，由存在一個名為 s_list 的檔案且內容如上所述來定義。

初始上下文

Arjan 做了一個修改，該修改是在s_list中新增一行。他的新檔案如下所示

1 apples
2 bananas
3 beer
4 cookies
5 rice

當 Arjan 記錄這個變更（新增啤酒）時，我們生成了一個補丁，它不僅告訴我們 Arjan 添加了哪些內容（“啤酒”），還告訴我們他在哪裡添加了它們，即在s_list的第 3 行。我們可以說，在他的儲存庫中，我們已經從上下文 $o$ 轉移到上下文 $a$，透過一個補丁 A。我們可以使用緊湊的符號${}^{o}A^{a}$ 或使用下面的圖形表示來表示

補丁 A

順序補丁

從這個上下文開始，Arjan 可能會決定進行進一步的更改。他的新更改將是應用於先前補丁上下文的補丁。因此，如果 Arjan 在此基礎上建立了一個新的補丁$B$，它將把我們從上下文 $a$ 轉移到一個新的上下文 $b$。下一個補丁將把我們從這個上下文轉移到另一個新的上下文 $c$，等等。像這樣彼此應用的補丁稱為順序補丁。我們像下表中那樣以從左到右的順序書寫它們，要麼顯式地表示上下文，要麼為了簡潔而省略它們

帶上下文	無上下文（簡寫）
${}^{o}A^{a}$	$A$
${}^{o}A^{a}B^{b}$	$AB$
${}^{o}A^{a}B^{b}C^{c}$	$ABC$

所有 darcs 倉庫都是簡單的補丁序列，如上所示；但是，當執行像撤銷或與其他使用者交換補丁這樣的複雜操作時，我們必須擁有一種機制來重新排列補丁並將它們放到不同的順序中。Darcs 補丁理論本質上是關於對補丁和補丁樹可以被操作和轉換的方式給出精確的定義，同時保持倉庫的一致性。

逆

讓我們回到本模組開頭的那一個例子。Arjan 剛剛在我們的駭客馬拉松購物清單中添加了啤酒，但是他突然間變得猶豫不決，想撤銷他的修改。在這個例子中，這可能包括啟動他的文字編輯器，從購物清單中刪除那行內容。但是如果他的修改很複雜，難以跟蹤呢？更好的做法是讓 darcs 自己解決。Darcs 透過計算一個逆補丁來做到這一點，也就是說，一個補丁，它執行的修改與另一個補丁完全相反

定義（補丁的逆）:

補丁 $P$ 的逆是 $P^{-1}$，它是唯一的一個補丁，它與補丁 $P$ 的組合 $PP^{-1}$ 對上下文不做任何修改，並且逆的逆是原始補丁。

所以上面，我們說 Arjan 建立了一個補丁 $A$，它將啤酒新增到購物清單中，從上下文 $o$ 轉變到上下文 $a$，或者更簡潔地說，${}^{o}A^{a}$。現在我們要建立逆補丁 $A^{-1}$，它刪除購物清單中的啤酒，並將我們帶回到上下文 $o$。在簡潔的上下文-補丁表示法中，我們將它寫成 ${}^{o}A^{a}{A^{-1}}^{o}$。在圖形上，我們將這種情況表示如下

逆補丁執行另一個補丁的相反修改

補丁逆可能看起來微不足道，但正如我們將在本模組後面看到的那樣，它們是一個基本操作，對使一些更高階的功能（如合併）正常工作至關重要。我們對 darcs 強加的規則之一是每個補丁都必須有一個逆。這些規則就是我們所說的補丁屬性。補丁屬性告訴我們關於補丁的哪些事情必須為真，才能讓 darcs 正常工作。人們通常喜歡夢想著設計出新的補丁型別來擴充套件 darcs 的功能，而定義這些補丁屬性就是我們如何知道他們的新補丁型別在 darcs 下會表現得正常。這些屬性中的第一個非常簡單

交換

阿詹很幸運能儘快意識到他想撤銷他的更改。但如果他意識到自己的錯誤慢一點會發生什麼？如果他在意識到自己想撤銷第一個更改之前進行了其他更改怎麼辦？是否可以在不撤銷所有後續更改的情況下撤銷他的第一個更改？有時可以，但要做到這一點，我們需要定義一個稱為 **交換** 的操作。

考慮上面示例的一個變體。像往常一樣，阿詹將啤酒新增到購物清單中。接下來，他決定在檔案的第 5 行新增一些義大利麵

啤酒和義大利麵

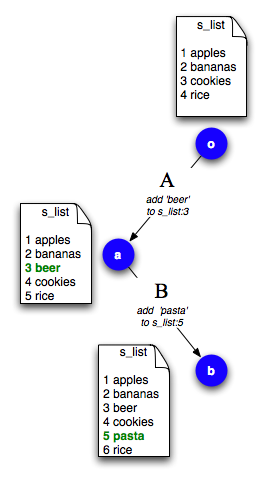
問題是，如果阿詹現在決定他畢竟不想在購物清單中新增啤酒，darcs 應該如何表現？阿詹只想刪除新增啤酒的補丁，而無需觸碰新增義大利麵的補丁。問題是 darcs 儲存庫是簡單、愚蠢的補丁序列。我們不能只是刪除啤酒補丁，因為那樣就沒有義大利麵補丁的上下文了！阿詹的第一個補丁 $A$ 將我們帶到上下文 $a$ ，如下所示：${}^{o}A^{a}$ ，他的第二個補丁將我們帶到上下文 $b$ ，值得注意的是從初始上下文 $a$ 開始：${}^{a}B^{b}$ 。刪除補丁 $A$ 將會從補丁 $B$ 下撤掉地毯。這裡的訣竅是，以某種方式 **改變** 補丁 $A$ 和 $B$ 的 **順序** 。這正是交換的作用。

為什麼不保留我們舊的補丁呢？

要理解交換，你應該理解為什麼我們不能保留我們最初的補丁，而是被迫依賴邪惡的繼女。使用上面啤酒和義大利麵的具體示例會有所幫助。雖然我們可以寫出序列 $AB$ 來表示先新增啤酒，然後新增義大利麵，簡單地寫下 $BA$ 來表示先新增義大利麵，然後新增啤酒，這將是一件非常愚蠢的事情。

這麼說吧：如果我們把 $B$ 應用在 $A$ 之前會發生什麼？我們在檔案的第 5 行添加了麵條

1 apples
2 bananas
3 cookies
4 rice
5 pasta

你有沒有覺得哪裡不對勁？我們接著在第 3 行添加了啤酒。如果你注意最終結果的內容，你可能會注意到我們列表的順序稍微錯了。比較這兩個列表看看原因

$BA$ （錯誤！）	$AB$ （正確）
1 apples 2 bananas 3 beer 4 cookies 5 rice 6 pasta	1 apples 2 bananas 3 beer 4 cookies 5 pasta 6 rice

這可能無關緊要，因為它只是一個購物清單，但想象一下，這是你的博士論文，或者你的計算機程式是為了終結世界飢餓。這個錯誤更加令人擔憂，因為它很微妙，人眼很難發現。

問題在於上下文，具體來說，$A$ 和 $B$ 之間的上下文。為了讓像“在 s_list 的第 5 行新增麵條”這樣的指令有意義，它們必須處於正確的上下文。幸運的是，交換很容易實現，它會產生兩個新的補丁 $B_{1}$ 和 $A_{1}$，它們執行與 $A$ 和 $B$ 相同的更改，但它們之間的上下文不同。

練習
補丁 $A_{1}$ 與 $A$ 相同。它在購物清單的第 3 行添加了“啤酒”。但是補丁 $B_{1}$ 應該做什麼？

還有一個重要的細節需要注意！我們之前說過，獲得正確的上下文是交換背後的動機——我們不能簡單地以不同的順序應用補丁 $AB$，因為這樣會使上下文完全錯誤。但上下文不會影響 A 和 B 是否可以交換（或如何交換）。這純粹是區域性的事情。相反，A 和 B 的交換也不會影響全域性上下文：序列 $AB$ 和 $B_{1}A_{1}$（後者是前者的交換）從相同的上下文開始，並以相同的上下文結束。

重新審視複雜的撤消

既然我們知道了交換操作的作用，讓我們看看如何使用它來撤消一個被其他補丁覆蓋的補丁。我們首先做的是交換 Arjan 的啤酒和麵條補丁。這給了我們到達相同上下文的另一種路線。但請注意 $B$ 和 $B_{1}$ 之間的細微差別！

交換給了我們兩種到達同一個補丁的方法

將補丁進行交換的目的是將補丁$A$推送到列表末尾，這樣我們就可以簡單地應用其逆運算。只是這裡，我們想要的不是$A$的逆運算，而是其邪惡的繼姐$A_{1}$的逆運算。應用該逆運算會發生以下情況：它會將我們帶回到上下文$b1$，就好像我們只應用了義大利麵補丁，但沒有應用啤酒補丁一樣。

交換給了我們兩種到達同一個補丁的方法

現在撤銷操作已經完成。總結一下，當我們想要撤銷的補丁被其他補丁埋藏時，我們會使用交換操作將其擠到補丁序列的末尾，然後計算交換後的補丁的逆運算。對於那些更注重順序的人來說，一般方案看起來是這樣的

使用交換操作處理複雜的撤銷操作

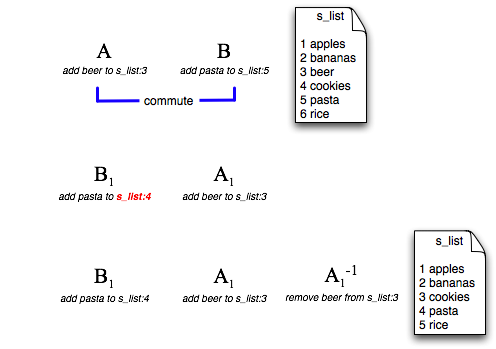
練習
想象一下相反的情況：Arjan 首先在列表中添加了義大利麵，然後又添加了啤酒。 如果沒有交換操作，如果他嘗試刪除義大利麵補丁而不是啤酒補丁，具體會發生什麼情況？ 使用交換操作來解決此撤銷操作。注意行號。

交換操作和補丁

每次我們定義一種補丁型別時，我們都必須定義它如何與其他補丁交換。大多數情況下，這非常簡單。例如，當交換兩個塊補丁時，我們只需要調整它們的行偏移量。例如，我們想要在檔案中的第 3 行新增內容，但如果我們使用補丁$Y$在該行之前插入一行，原本的第 3 行現在就變成了第 4 行！因此，補丁$X_{1}$將 "x" 插入到第 4 行，就像$X$將 "x" 插入到第 3 行一樣。

有些補丁無法交換。例如，你不能將新增檔案與向其中新增內容的補丁進行交換。但現在，我們將重點關注可以交換的補丁。

合併

注意：這裡可能是休息一下的好地方。我們將進入一個新的主題以及新的（但相似）的示例。

我們已經介紹了兩個基本的 Darcs 操作：補丁逆運算和補丁交換操作。事實證明，這兩個操作幾乎是我們執行 Darcs 合併所需要的一切。

Arjan 和 Ganesh 正在一起構建一個購物清單，用於即將到來的 Darcs 駭客馬拉松。Arjan 初始化了倉庫並添加了一個名為 s_list 的檔案，內容如下

1 apples
2 bananas
3 cookies
4 rice

然後他記錄了他的更改，Ganesh 執行了 darcs get 命令以獲取他的倉庫的相同副本。請注意，Arjan 和 Ganesh 從相同的上下文開始。

初始上下文

Arjan 做了一個修改，該修改是在s_list中新增一行。他的新檔案如下所示

1 apples
2 bananas
3 beer
4 cookies
5 rice

Arjan 的補丁將他帶到了一個新的上下文$a$

補丁 A

現在，在 Ganesh 的倉庫中，他也進行了一項修改；他認為 s_list 很難理解，因此將檔名重新命名為 shopping。請記住，此時，Ganesh 還沒有看到 Arjan 的修改。他仍然從原始上下文$o$開始，並透過他的補丁$B$移動到了一個新的上下文$b$

補丁 B

並行補丁

此時，Ganesh 決定獲得 Arjan 更改的副本會很有用。粗略地說，我們想要將 Arjan 的補丁 A 拉入 Ganesh 的倉庫 B。但是，存在一個主要問題！即，Arjan 的補丁將我們從上下文$o$帶到了上下文$a$。將其拉入 Ganesh 的倉庫中將涉及嘗試將其應用到上下文$b$，而我們根本不知道如何做到這一點。換句話說：Arjan 的補丁告訴我們向檔案 s_list 新增一行；但是，在 Ganesh 的倉庫中，s_list 不再存在，因為它已經被移動到了 shopping。我們如何知道 Arjan 的更改（新增一行 "beer"）應該應用於新的檔案 shopping 而不是 s_list 呢？

Ganesh 嘗試從 Arjan 拉取程式碼

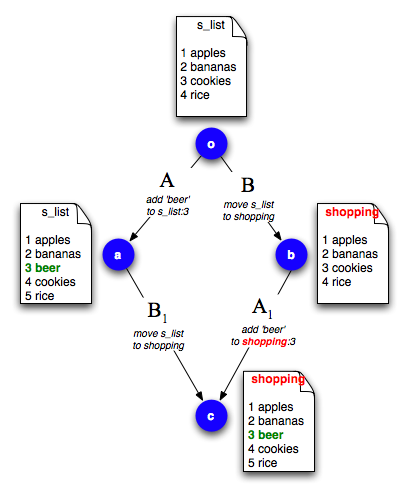
Arjan 和 Ganesh 的補丁從相同的上下文 o 開始，並分叉到不同的上下文 a 和 b。我們說他們的補丁彼此**平行**，並將其寫為 $A\vee B$。在嘗試從 Arjan 的倉庫中拉取補丁時，我們正在嘗試合併這兩個補丁。基本方法是將並行補丁轉換為順序補丁 $BA_{1}$，這樣 $A_{1}$ 與 $A$ 基本上做著相同的更改，但在 b 的上下文中。我們希望產生這種情況 ${}^{o}{B^{b}}{A_{1}^{c}}$

執行合併

將 Arjan 和 Ganesh 的並行補丁轉換為順序補丁只需要我們在本模組前面描述的逆和交換操作。

1. 所以我們從 Ganesh 的補丁開始。在上下文表示法中，我們位於 ${}^{o}{B}^{b}$
2. 我們計算逆補丁 $B^{-1}$。序列 $BB^{-1}$ 包括將 s_list 移動到購物，然後又移回來。我們回到了最初的上下文：${}^{o}{B}^{b}{B^{-1}}^{o}$
3. 現在我們可以毫無顧慮地應用 Arjan 的補丁：${}^{o}{B}^{b}{B^{-1}}^{o}A^{a}$，但結果看起來並不那麼有趣，因為我們基本上得到了與 Arjan 現在相同的東西，而不是合併。
4. 我們只需要交換最後兩個補丁，${B}^{-1}{A}$，得到一對新的補丁 ${A_{1}}{B_{1}}^{-1}$。儘管如此，最終結果看起來並不那麼有趣，因為它導致了與上一步完全相同的 state：${}^{o}{B}^{b}{A_{1}}^{c}{{B_{1}}^{-1}}^{a}$
5. 然而，一個關鍵的區別是，倒數第二個補丁恰好產生了我們想要的那個狀態！現在我們所要做的就是丟棄 ${B_{1}}^{-1}$ 補丁，它只是在撤銷Ganesh寶貴的成果。也就是說，透過簡單地確定如何生成一個與 $B$ 可交換的 $A_{1}$，我們就確定了將更新Ganesh倉庫的 $A$ 版本。

透過逆運算和交換進行合併

所有這些的最終結果是，我們得到了我們想要的補丁， $A_{1}$，以及一個成功的合併。

我們想要一個新的補丁A_1

合併是對稱的

合併是對稱的

具體來說，我們討論了Ganesh將Arjan的補丁拉入他的倉庫，那麼反過來呢？Arjan將Ganesh的補丁拉入他的倉庫將以完全相同的方式進行，只是他正在尋找一個Ganesh補丁 $B_{1}$ 的交換版本，該版本將應用於他的倉庫。如果Ganesh可以拉入Arjan的補丁，那麼Arjan也可以拉入Ganesh的補丁，結果將完全相同。

合併是對稱的

定義（兩個補丁的合併）:

兩個補丁 $A$ 和 $B$ 的合併結果是兩個補丁中的一個： $A_{1}$ 和 $B_{1}$，它們滿足關係 $A\vee B\Longrightarrow B{A_{1}}\leftrightarrow A{B_{1}}$

合併定義描述了將兩個並行補丁組合成補丁序列時應該發生的事情。內建的對稱性對於darcs來說是至關重要的，因為darcs倉庫完全由它的補丁定義。換句話說，

待寫

與逆運算的交換性

合併的定義告訴我們我們想要合併看起來像什麼。我們怎麼會知道如何實際執行合併呢？答案來自交換和逆運算的以下性質：如果你可以將補丁 $A^{-1}$ 的逆運算與另一個補丁 $B$ 進行交換，那麼你也可以將補丁本身與 $B_{1}$ 進行交換。

請注意，此屬性的左側完全符合合併定義中要求的關係。要了解為什麼這一切有效，

待寫

定義和屬性

逆定義	$AA^{-1}$ 沒有效果
逆的逆	$(A^{-1})^{-1}=A$
逆複合屬性	$(AB)^{-1}=B^{-1}A^{-1}$
交換定義	$AB\leftrightarrow {B_{1}}{A_{1}}$
合併定義	$A\vee B\Longrightarrow B{A_{1}}\leftrightarrow A{B_{1}}$
逆交換屬性	$B{A_{1}}\leftrightarrow A{B_{1}}$ 當且僅當 ${B_{1}}{A_{1}}^{-1}\leftrightarrow {A^{-1}}B$