維基少年:兒童程式設計/設計你的解決方案

維基少年：兒童程式設計
瞭解你的問題	設計你的解決方案	自上而下還是自下而上？

一旦我們弄清楚了我們的問題，我們就需要設計一個解決問題的方法。在這個階段，我們還沒有編寫任何程式碼。我們只是在制定一個框架，我們將在演算法設計階段遵循這個框架。

分治法

分治法 (D&C) 來自拉丁語 divide et impera。它指的是將一個大問題分解成更小的子問題。子問題可以進一步細分為更小的子子問題，然後變成子子子問題，等等，你懂的。分治法是一種系統化的方式，可以為你的解決方案提供一個藍圖。在每個子問題都解決後，我們將它們合併在一起，形成“大局”。

分治法可以應用於現實生活中的問題和程式設計問題。我們將在下一節中檢視一個著名的應用程式，陣列排序。現在，讓我們嘗試一些更簡單的事情。假設你想測量一個體育場的面積。沒有直接計算體育場大小的公式，所以讓我們嘗試這樣操作

此圖是一個結構圖。結構圖是對映解決方案結構的一種方式。（不意外吧！）

讓我們嘗試一個更難的問題。假設你有一個方形的花壇和一個圍繞它的路徑。你需要鋪設這條路，並想計算這個專案的總成本。你會怎麼做？

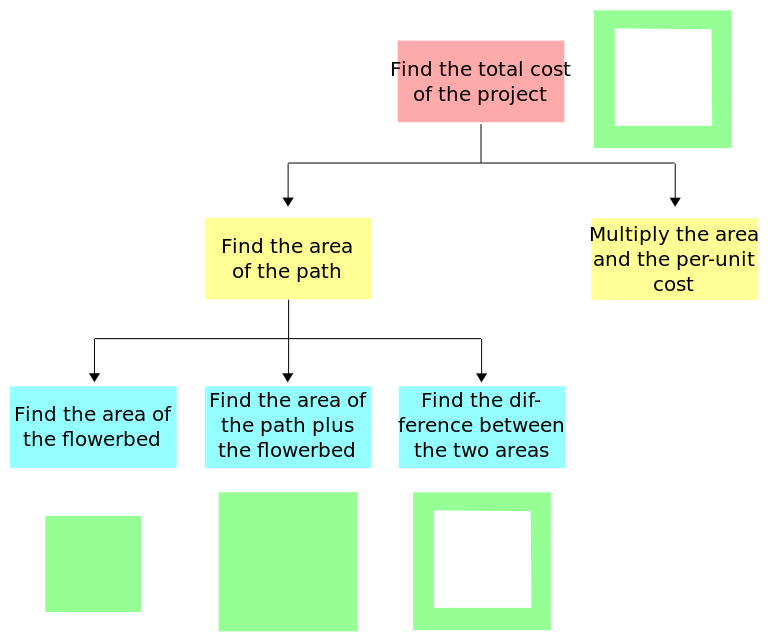
請注意，這個問題涉及將問題分解成更小的子問題。

模組化方法

透過對我們的問題使用 D&C，我們正在採用模組化方法進行程式設計。在上面的圖表中，每個塊代表一個模組。在第二個圖表中，可以將子子問題稱為子模組。將問題分解成不同的模組是一種常見的程式設計實踐。

資料和資訊在結構圖中以某種方式流動。例如，在花壇示例中，'查詢兩個區域之間的差異' 模組需要知道 '查詢花壇區域' 和 '查詢路徑加花壇區域' 模組中的資料。為了清晰地表示這一點，每個模組都有一個模組規範，它清楚地記錄了模組的輸入、輸出和過程。我們也可以為此目的使用 I-P-O 圖表。讓我們看一下花壇專案的模組規範。（如果你沒有完全理解所有內容，不要擔心；我們很快就會看到它們。）

模組：'查詢專案的總成本'
輸入	過程	輸出
花壇的寬度花壇的長度整個區域的寬度整個區域的長度每單位成本	提示使用者輸入花壇的尺寸、整個區域的尺寸和每單位成本獲取花壇的尺寸、每單位成本的尺寸驗證輸入資料查詢路徑的面積將面積和每單位路徑相乘將專案的總成本輸出到螢幕上	專案的總成本

模組：'查詢路徑的面積'
輸入	過程	輸出
花壇的寬度花壇的長度整個區域的寬度整個區域的長度	讀取花壇的尺寸、整個區域的尺寸查詢花壇的面積查詢路徑面積加上花壇面積查詢兩個區域之間的差異輸出路徑的面積	花壇的面積

模組：'將面積乘以每單位成本'
輸入	過程	輸出
路徑的面積每單位成本	讀取路徑的面積和每單位成本根據需要轉換路徑和成本的單位將路徑的面積乘以每單位成本輸出專案成本	專案的總成本

模組：'查詢花壇的面積'
輸入	過程	輸出
花壇的長度花壇的寬度	讀取花壇的尺寸將路徑的長度和寬度相乘輸出花壇的面積	花壇的面積

模組：'查詢路徑加花壇的面積'
輸入	過程	輸出
整個區域的長度花壇的寬度	讀取整個區域的尺寸將路徑的長度和寬度相乘輸出整個區域	花壇的面積

模組：'查詢兩個區域之間的差異'
輸入	過程	輸出
花壇的面積整個區域	讀取兩個區域查詢兩個區域之間的差異輸出路徑的面積	路徑的面積

模組化方法有很多優點。

它允許在程式設計中更加靈活。模組化方法促進了程式碼重用。有時，一個模組可能在一個程式中被使用多次。例如，在一個幾何程式中，希望有一個單一的模組用於勾股定理，它可以在程式中的任何時候使用。這可以節省我們複製貼上（並且可能會在此過程中出錯）的時間。此外，一個模組的更改可能不會對整個程式產生重大影響。

一次解決一個小問題更容易。如果我們將程式分成各個模組，更容易看到程式的結構。一大塊程式碼很難閱讀和除錯。將其分成更小的部分有助於識別和糾正錯誤。
它鼓勵程式設計師之間的協作。一群程式設計師可以將工作分配到不同模組，並將其分配給每個人。它還促進專業化：例如，一個熟悉 XML DOM 的程式設計師可以選擇從事 XML 方面的工作，而另一個熟悉 SQL 的程式設計師可以選擇從事資料庫和 PHP 方面的工作。它還便於管理和控制。

模組化方法也有缺點。例如，每個團隊成員可能不清楚整個程式是如何工作的。因此，他們可能不知道全貌。這可能會導致不同模組之間的連結出現問題。它還需要為其他程式設計師進行大量深入的文件記錄，這會增加時間和成本。

等等...

我們已經使用模組化方法設計了程式的框架，但我們應該從哪裡開始呢？我們應該先處理最小的程式，然後逐步向上嗎？還是應該先處理最上面的部分，然後逐步向下？閱讀下一章，找出答案！