數字系統
數學是計算機科學研究的基礎。重要的是,所使用的數學必須明確定義且沒有歧義。這從作為數學一部分的數字的定義開始。
這些定義使用集合來描述,其中將單獨的物體(在本例中是數字本身)收集在一起以形成一個新的描述性物體。從 0 到 10 的奇數集合可以描述為
O = {1, 3, 5, 7, 9}
O 是集合的名稱,數字是形成該集合的物體。
數學的基礎是計數物體。孩子們從小就學習,不同的物體數量可以用不同的名稱來描述,例如五個橘子或十個香蕉。
自然數集 ℕ 包含所有正整數(整數),以及數字 0,可以描述為
ℕ = {0, 1, 2, 3, ...}
請注意,數字是無限的,因此不可能完全定義該集合。在這種情況下,定義前幾個值是完全可以接受的。
為了擴充套件這一點,我們可以包括負值。整數是既可以是正數也可以是負數的整數
ℤ = {..., -3, -2, -1 , 0, 1, 2, 3, ...}
擴充套件來說,它們包括之前定義的自然數。
數字也可以表示為分數。這包括整數和小數部分的數字。例如,整數 5 也可以表示為分數 5/1(它是一個有理數),就像值 1.5 將表示為分數 3/2 一樣。我們可以描述一部分有理數集,如下所示
ℚ = {..., -1/3, -1/2, -1/1 , 0, 1/1, 1/2, 1/3, ...}
與之前的集合一樣,有理數是無限的。
有些數字不能表示為分數。當有理數表示為十進位制值時,它們的小數點後將有確定的位數。1/4 是一個有理數,這將表示為十進位制值 0.25。帶有迴圈小數部分的數字也是有理數。1/3 將表示為小數 0.3 ̇。
這些數字不以集合的形式描述,因為它們是特殊情況。經常使用的常見無理數使用單獨的符號描述
π (Pi) √2 e (Euler's number) φ (Golden ratio)
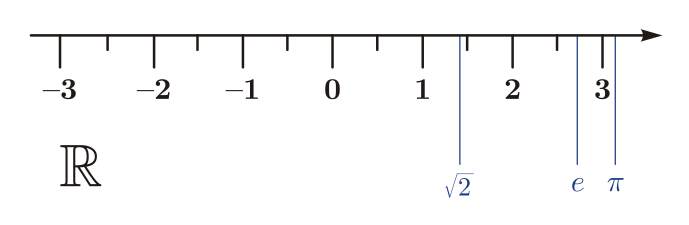
上面描述的所有數字集合都被認為是實數集 ℝ。在數軸上,實數值將是數軸上的任何值。
在一組有序值中,序數表示值的順序。因此,在集合 S = {"alpha", "beta", "gamma"} 中,物件 "alpha" 是第 1 個,"beta" 是第 2 個,依此類推。
這些數字集的應用可以在現實世界中看到。自然數用於計數可以觀察到的物體,例如桌上的蘋果數量
同樣,實數用作度量,因為它們能夠量化這些值以包含小數部分。
|
練習:識別以下值的所有可能的數字系統 34 答案 自然數、整數、實數 π 答案 無理數、實數 9/1 答案 有理數、自然數、整數、實數 1/9 答案 有理數、實數 第 3 個 答案 序數 |