A-level 數學/CIE/純數學 2/三角函式

正割、餘割和餘切

正割

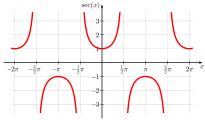
一個角的正割是其餘弦的倒數。

$\sec x={\frac {1}{\cos x}}$

餘割

一個角的餘割是其正弦的倒數。

$\operatorname {cosec} x={\frac {1}{\sin x}}$

餘切

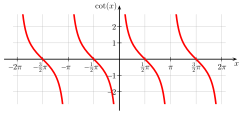
一個角的餘切是其正切的倒數。

$\cot x={\frac {1}{\tan x}}$

圖形

• 
  sec x 圖形
• 
  cosec x 圖形
• 
  cot x 圖形

用正割、餘割和餘切解方程

用正割、餘割或餘切解方程的方法與其他三角方程基本相同。

例如，解 $-\sec x=2+\cos x$，其中 $0<x<2\pi$

${\begin{aligned}-\sec x&=2+\cos x\\-1&=2\cos x+\cos ^{2}x\\\cos ^{2}x+2\cos x+1&=0\\(\cos x+1)^{2}&=0\\\cos x+1&=0\\\cos x&=-1\\x&=\pi \end{aligned}}$

恆等式

餘切恆等式

$\tan x\equiv {\frac {\sin x}{\cos x}}$ 以及 $\cot x\equiv {\frac {1}{\tan x}}$，因此 $\cot x\equiv {\frac {\cos x}{\sin x}}$

勾股定理推導的恆等式

勾股定理三角恆等式指出 $\sin ^{2}x+\cos ^{2}x\equiv 1$。我們可以將兩邊都除以 $\cos ^{2}x$ 以獲得另一個恆等式：$\tan ^{2}x+1\equiv \sec ^{2}x$。或者，我們可以將兩邊都除以 $\sin ^{2}x$ 以獲得 $1+\cot x\equiv \operatorname {cosec} x$.

加法公式

當我們對和或差應用三角函式時，使用加法公式，例如 $\sin(\theta +{\frac {\pi }{6}})$.

對於正弦、餘弦和正切，加法公式為：

${\begin{aligned}\sin(A\pm B)&=\sin A\cos B\pm \cos A\sin B\\\cos(A\pm B)&=\cos A\cos B\mp \sin A\sin B\\\tan(A\pm B)&={\frac {\tan A\pm \tan B}{1\mp \tan A\tan B}}\end{aligned}}$

二倍角公式

二倍角公式是加法公式的特例，當和中的兩個項相等時。

${\begin{aligned}\sin(2A)&=\sin(A+A)=\sin A\cos A+\sin A\cos A=2\sin A\cos A\\\cos(2A)&=\cos(A+A)=\cos A\cos A-\sin A\sin A=\cos ^{2}A-\sin ^{2}A=2\cos ^{2}A-1=1-2\sin ^{2}A\\\tan(2A)&=\tan(A+A)={\frac {\tan A+\tan A}{1-\tan A\tan A}}={\frac {2\tan A}{1-\tan ^{2}A}}\end{aligned}}$

將 $a\sin \theta +b\cos \theta$ 轉換為 $R\sin(\theta \pm \alpha )$ 或 $R\cos(\theta \pm \alpha )$

在解三角方程時，將表示式轉換為單項式非常有用。為了做到這一點，我們可以使用加法公式。

例如，求解 $\sin \theta +{\sqrt {3}}\cos \theta =1$，其中 $0<\theta <2\pi$

${\begin{aligned}\sin \theta +{\sqrt {3}}\cos \theta &=R\sin(\theta +\alpha )\\\sin \theta +{\sqrt {3}}\cos \theta &=R\sin \theta \cos \alpha +R\cos \theta \sin \alpha \\{\text{Equate coefficients of }}\sin \theta \to \quad R\cos \alpha &=1\\{\text{Equate coefficients of }}\cos \theta \to \quad R\sin \alpha &={\sqrt {3}}\\\tan \alpha &={\frac {R\sin \alpha }{R\cos \alpha }}={\frac {\sqrt {3}}{1}}\\\therefore \alpha &={\frac {\pi }{3}}\\R\cos({\frac {\pi }{3}})&=1\\R&={\frac {1}{\tfrac {1}{2}}}=2\\2\sin(\theta +{\frac {\pi }{3}})&=1\\\sin(\theta +{\frac {\pi }{3}})&={\frac {1}{2}}\\\theta +{\frac {\pi }{3}}&=\left\{{\frac {5\pi }{6}},{\frac {13\pi }{6}}\right\}\leftarrow {\text{Be careful with the domain of }}\theta +{\frac {\pi }{3}}\\\theta &=\left\{{\frac {3\pi }{6}},{\frac {11\pi }{6}}\right\}\end{aligned}}$

使用 $R\cos(\theta \pm \alpha )$ 非常相似。

例如，求解 ${\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta =1$ 在 $0<\theta <2\pi$ 範圍內的解。

${\begin{aligned}{\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta &=R\cos(\theta -\alpha )\\{\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta &=R\cos \theta \cos \alpha +R\sin \theta \sin \alpha \\{\text{Equate coefficients of}}\sin \theta \to \quad R\sin \alpha &={\sqrt {2}}\\{\text{Equate coefficients of}}\cos \theta \to \quad R\cos \alpha &={\sqrt {2}}\\\tan \alpha &={\frac {R\sin \alpha }{R\cos \alpha }}={\frac {\sqrt {2}}{\sqrt {2}}}=1\\\therefore \alpha &={\frac {\pi }{4}}\\R\sin \left({\frac {\pi }{4}}\right)&={\sqrt {2}}\\R\left({\frac {1}{\sqrt {2}}}\right)&={\sqrt {2}}\\R&={\sqrt {2}}({\sqrt {2}})=2\\2\cos(\theta -{\frac {\pi }{4}})&=1\\\cos(\theta -{\frac {\pi }{4}})&={\frac {1}{2}}\\\theta -{\frac {\pi }{4}}&=\left\{{\frac {\pi }{3}},{\frac {5\pi }{3}}\right\}\\\theta &=\left\{{\frac {7\pi }{12}},{\frac {23\pi }{12}}\right\}\end{aligned}}$

備註