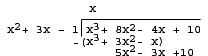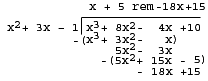A-level 數學/OCR/C4/代數與圖

有理表示式

有理表示式在分子和分母中有多項式：${\frac {f\left(x\right)}{g\left(x\right)}}$. 在某些情況下，有理函式可以簡化，這使得微分、積分和簡單的求解方程變得更容易。 如果你想簡化一個分數，有一個簡單的步驟可以遵循。

1. 完全分解分子和分母。

   ${\frac {ax^{3}+bx^{2}+cx+d}{ax^{2}+bx+c}}={\frac {(ex+f)(x+g)(x+h)}{(ix+j)(x+g)(x+h)}}$

2. 如果分子和分母中有相同的因式，你可以將它們抵消。

   ${\frac {(ex+f){\cancel {(x+g)}}{\cancel {(x+h)}}}{(ix+j){\cancel {(x+g)}}{\cancel {(x+h)}}}}={\frac {(ex+f)}{(ix+j)}}$

3. 如果還有多個剩餘的因式，你可以根據情況重新組合。

例子

簡化以下表達式：${\frac {5x^{3}+40x^{2}+75x}{x^{2}+12x+35}}$.

1. 分解分子和分母，注意分子中可以提取出 5x。

   ${\frac {5x(x^{2}+8x+15)}{(x+5)(x+7)}}={\frac {5x(x+5)(x+3)}{(x+5)(x+7)}}$

2. 抵消相同的因式

   ${\frac {5x(x+5)(x+3)}{(x+5)(x+7)}}={\frac {5x(x+3)}{(x+7)}}$

3. 重新組合因式

   ${\frac {5x(x+3)}{(x+7)}}={\frac {5x^{2}+15x}{x+7}}$

多項式的除法

在核心四中，您將需要用線性或二次多項式除以最多四次的多項式。 這隻有在分子大於分母的情況下才能工作。 結果將始終採用以下形式；${\frac {f(x)}{g(x)}}=q(x)+{\frac {r(x)}{g(x)}}$ 其中 q(x) 是結果多項式，而 ${\frac {r(x)}{g(x)}}$ 是餘數。

長除法

多項式長除法與普通長除法非常相似。 我將用一個問題來演示長除法的工作原理。

用 $x^{2}+3x-1$ 除以 $x^{3}+8x^{2}-4x+10$。

第一步是設定方程。 確保它是從 x 的最高次冪到 x 的最低次冪的順序。

然後我們用除數的第一項除以被除數的第一項。

${\frac {x^{3}}{x^{2}}}=x$

我們將這個結果放在頂部。

然後我們將結果乘以除數，並從被除數中減去它。

$x\left(x^{2}+3x-1\right)=x^{3}+3x^{2}-x$

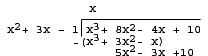
剩下的部分成為新的被除數，我們再次重複這個過程。 我們繼續這樣做，直到第一項的次數小於除數的第一項的次數。 剩下的部分是餘數。

綜合除法

示例一

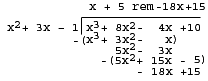
用 x-3 除以 $2x^{5}+5x^{2}-10x^{3}-30x-171$。

除數是 c。 所以在這種情況下它將是 3。

然後我們需要從最高次冪到最低次冪排列我們的除數，如果缺少次冪，則用零替換它。

$2x^{5}+0x^{4}-10x^{3}+5x^{2}-30x-171$

然後我們只看係數。

2 + 0 - 10 + 5 - 30 - 171

現在我們設定我們的除法方程。

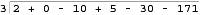
接下來我們向上搬運除數的第一項。

然後我們將結果乘以除數，並將其加到下一項。

我們繼續這樣做，直到到達結尾。

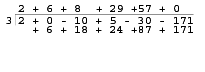
現在我們需要讀取變數。 當我們讀取變數時，我們從最高次冪 -1 到最低次冪。 最後一個數字是餘數。

$2x^{4}+6x^{3}+8x^{2}+29x+57$ 餘數 0。

這是問題的答案。

部分分式

只有真分數才能分解成部分分數。真分數是指分子次數小於分母次數的分數。部分分數可用於簡化微分、積分或級數運算。部分分數分解的目標是將一個複雜的多分式分解成多個較簡單的多分式。為了建立部分分數分解方程，您需要：

1. 對分子和分母進行因式分解。

   ${\frac {ax^{2}+bx+c}{ax^{3}+bx^{2}+cx+d}}\equiv {\frac {(ix+j)(kx+l)}{(ax+b)(cx+d)(ex+f)}}$

2. 透過將每個因式作為分母，並在分子上使用一個唯一的變數，來建立部分分數。

   ${\frac {(ix+j)(kx+l)}{(ax+b)(cx+d)(ex+f)}}\equiv {\frac {A}{(ax+b)}}+{\frac {B}{(cx+d)}}+{\frac {C}{(ex+f)}}$

3. 將每個分數乘以原始分數的分母。

   ${\frac {(ix+j)(kx+l)(ax+b)(cx+d)(ex+f)}{(ax+b)(cx+d)(ex+f)}}\equiv$

   ${\frac {A(ax+b)(cx+d)(ex+f)}{(ax+b)}}+{\frac {B(ax+b)(cx+d)(ex+f)}{(cx+d)}}+{\frac {C(ax+b)(cx+d)(ex+f)}{(ex+f)}}$

4. 取消所有相同的因式。

   $(ix+j)(kx+l)\equiv A(cx+d)(ex+f)+B(ax+b)(ex+f)+C(ax+b)(cx+d)$

5. 將所有因式相乘。

   $ikx^{2}+ilx+jlx+jl\equiv$

   $(Acex^{2}+Acfx+Adex+Adf)+(Baex^{2}+Bafx+Bbex+Bbf)+(Cacx^{2}+Cadx+Cbdx+Cbd)\,}$

6. 將所有具有相同指數的 x 項分組在一起。

   $ikx^{2}+(il+kj)x+jl\equiv$

   $(Ace+Bae+Cac)x^{2}+\left(Acf+Ade+Baf+Bbe+Cad+Cbd\right)x+\left(Adf+Bbf+Cbd\right)$

7. 等式兩邊相同指數的 x 係數相等。利用這一事實，使用聯立方程求解分子中的變數。這種方法稱為係數比較法。

   $ik\equiv \left(Ace+Bae+Cac\right)$

   $\left(il+kj\right)\equiv \left(Acf+Ade+Baf+Bbe+Cad+Cbd\right)$

   $jl\equiv \left(Adf+Bbf+Cbd\right)$

8. 在步驟 2 中，用上一步獲得的變數值替換變數 A、B、C。

示例一

將以下表達式改寫成部分分式：${\frac {x^{2}+13x+40}{2x^{3}+27x^{2}+111x+140}}$.

1. 利用進一步純化 1：多項式方程的根 中的知識。我們可以將分母分解如下。

   ${\frac {x^{2}+13x+40}{2x^{3}+27x^{2}+111x+140}}\equiv {\frac {(x+5)(x+8)}{(2x+5)(x+7)(x+4)}}$

2. 現在我們開始進行部分分式分解。

   ${\frac {x^{2}+13x+40}{(2x+5)(x+7)(x+4)}}\equiv {\frac {A}{(2x+5)}}+{\frac {B}{(x+7)}}+{\frac {C}{(x+4)}}$

3. 接下來，我們將原始表示式的所有項乘以分母。

   ${\frac {x^{2}+13x+40(2x+5)(x+7)(x+4)}{(2x+5)(x+7)(x+4)}}\equiv$

   ${\frac {A(2x+5)(x+7)(x+4)}{(2x+5)}}+{\frac {B(2x+5)(x+7)(x+4)}{(x+7}}+{\frac {C(2x+5)(x+7)(x+4)}{(x+4)}}$

4. 現在我們消去相同項。

   $(x+7)(x+8)\equiv A(x+7)(x+4)+B(2x+5)(x+4)+C(2x+5)(x+7)$

5. 然後將所有因子相乘。

   $x^{2}+13x+40=Ax^{2}+11Ax+28A+2Bx^{2}+13Bx+20B+2Cx^{2}+19Cx+35C\,$

6. 然後將各項歸類。

   $x^{2}+13x+40=(A+2B+2C)x^{2}+(11A+13B+19C)x+(28A+20B+35C)\,$

7. 現在我們對係數進行等式化。然後我們需要解聯立方程。

   $1\equiv (A+2B+2C)\equiv \,$

   $13\equiv (11A+13B+19C)\,$

   $40\equiv (28A+20B+35C)\,$

   1. 首先我們對A進行等式化。

      $1\equiv (A+2B+2C)\equiv A=1-2B-2C\,$

      然後

      $13\equiv 11(1-2B-2C)+13B+19C\equiv 11-22B-22C+13B+19C\equiv 11-9B-3C$

      $9B\equiv 3C+2$

      $B\equiv -{\frac {3C+2}{9}}$

   2. 我們可以進一步將A與

      $A\equiv 1-2(-{\frac {3C+2}{9}})-2C$

      $A\equiv {\frac {13-12C}{9}}$

   3. 現在我們可以解出C。

      $40\equiv (28({\frac {13-12C}{9}})+20(-{\frac {3C+2}{9}})+35C)\,$

      $40\equiv (({\frac {364-336C}{9}})+(-{\frac {60C+40}{9}})+35C)\,$

      $40=36-9C\,$

      $C={\frac {-4}{9}}$

   4. 現在我們可以求解其餘部分

      $A\equiv {\frac {13-12{\frac {-4}{9}}}{9}}={\frac {55}{27}}$

      $B\equiv -{\frac {3C+2}{9}}={\frac {-2}{27}}$

      $C\equiv {\frac {-4}{9}}$

8. 現在我們可以寫出我們的部分分式

   ${\frac {x^{2}+13x+40}{(2x+5)(x+7)(x+4)}}\equiv {\frac {55}{27(2x+5)}}-{\frac {2}{27(x+7)}}-{\frac {4}{9(x+4)}}$