A-level 數學/OCR/M1/力作為向量

向量

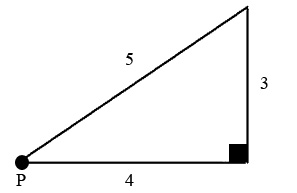
向量是一個既有大小（或尺寸）又有方向的量。向量的反義詞是標量。標量只有大小，沒有方向。例如，速度是一個標量，因為速度與方向無關。這最好用三角形來表示

我們的點 P 沿這個三角形的斜邊以$5ms^{-1}$ 的速度飛行。然而，它的速度並非 5。由於速度是一個向量，既有大小又有方向，因此 P 的速度等於沿水平方向以$4ms^{-1}$ 和沿垂直方向以$3ms^{-1}$ 的速度移動。

有多種不同的方法可以將它寫成向量。最常見的一種是使用i和j符號。其中i是速度的水平分量，j是速度的垂直分量。使用此符號，我們的飛機將具有 (4i + 3j) 的速度。

另一種常見的向量寫法是${x \choose y}$ 的形式，其中 x 是水平分量，y 是垂直分量。以我們的飛機為例，這種向量形式的速度將是${4 \choose 3}ms^{-1}$。

要將向量轉換為水平和垂直分量，我們

1. 畫一個代表向量的三角形。

2. 在三角形上標記所有已知的值。

3. 使用三角函式求解。

例如，大小為 25N 的力 P 方向為$arcsin$ ${\frac {7}{25}}$ （arcsin 是$sin$ 的反函式），求出 P 的水平和垂直分量。

三角形

標記三角形

使用三角函式：如果 $\arcsin \theta$ 是 ${\frac {7}{25}}$，那麼 $\theta$ 是 $sin$ ${\frac {7}{25}}$。正弦是O/H。因此，P的垂直分量是7。水平分量可以透過使用勾股定理或識別7、24、25為勾股三元組來找到。勾股定理指出 $a^{2}$+$b^{2}$=$c^{2}$，其中c是斜邊，a和b是鄰邊和對邊（順序無關）。因此，$\ 25^{2}-\ 7^{2}\$ = $horizontalcomponent^{2}$ = 576。 $576^{\frac {1}{2}}$ = 24。用 **i** 和 **j** 表示，結果是 (24i+7j)。