A-level 數學/OCR/M3/SHM

SHM 運動方程

定義運動方程（關於加速度和位移）

根據定義，當一個粒子執行簡諧運動 (SHM) 時

• 它的加速度大小 ${\ddot {x}}$ 與 它的位移大小 $x$ 從某個固定點，成正比，並且
• 它的加速度和位移方向相反。

更正式地說，當運動方程 ${\ddot {x}}=-kx$ 成立時，就會發生 SHM，其中 $k$ 是一個正常數。按照慣例，我們寫 $k=\omega ^{2}$（我們將稍後解釋 $\omega$ 的意義）因此方程變為 ${\ddot {x}}=-\omega ^{2}x$.

在現實世界中很容易找到簡諧振盪器。附著在彈性弦或彈簧上的質量的無阻尼振盪只是力學領域的一個例子。在研究這些例子之前，讓我們首先使用下面描述的抽象模型來檢查 SHM 的特徵。

考慮以下具有 $a$ 振盪幅度 的振盪器。令 $x$ 表示它相對於原點的位移，${\ddot {x}}$ 表示它的加速度。

讓我們重新說明 SHM 的定義方程

${\ddot {x}}=-\omega ^{2}x\,$

回想一下，表示位移及其關於時間的導數的代數變量表示一維向量量（即它們都位於一條直線上）。如果變數的值為正，則其向量指向正方向；如果為負，則其向量指向另一個方向。

觀察當 $x=0$ 時，則 ${\ddot {x}}=0$。根據牛頓第二定律，此時作用在振盪器上的合力 $F$ 為零。

當 $x>0$（即原點右側）時，合力指向左側，指向原點。當 $x<0$ 時，合力指向右側，指向原點。因為當振盪器不在原點時，合力總是指向原點，所以合力可以被稱為恢復力。恢復力的行為表明振盪器的速度在原點最大，在兩個方向改變的端點（即當 $v=0$ 時，$x=\pm a$）為零。

運動方程，關於速度、振幅和位移

現在，讓我們用速度 $v$ 和位移 $x$ 來改寫定義的 SHM 方程。我們進行以下替換：${\ddot {x}}={\frac {dv}{dt}}={\frac {dv}{dx}}{\frac {dx}{dt}}=v{\frac {dv}{dx}}$。因此，

	${\ddot {x}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	$v{\frac {dv}{dx}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	$\int v\,dv$	$=-\omega ^{2}\int x\,dx$（分離變數）

用 $v=0$ 和 $x=\pm a$ 作為積分的一對極限，我們得到

	$\int _{0}^{v}v\,dv$	$=-\omega ^{2}\int _{\pm a}^{x}x\,dx$
$\Rightarrow$	$\left[{\frac {1}{2}}v^{2}\right]_{0}^{v}$	$=-\omega ^{2}\left[{\frac {1}{2}}x^{2}\right]_{\pm a}^{x}$

$\Rightarrow$

$v^{2}=\omega ^{2}(a^{2}-x^{2})\,$

現在，很明顯當 $x=0$ 時（在這種情況下 $v=\pm \omega a$），速度達到最大值，而當 $x=\pm a$ 時 $v=0$。

運動方程，根據位移、振幅和時間

常數 $\omega$ 的重要性將在我們用位移 $x$ 和時間 $t$ 表示定義的 SHM 方程後變得清晰。

	${\ddot {x}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	${\frac {d^{2}x}{dt^{2}}}+\omega ^{2}x$	$=0\,$

這只是一個具有常數係數的二階常微分方程。特徵方程（作為 $m$ 的函式）由下式給出：

$m^{2}+\omega ^{2}=0\Rightarrow m=\pm {\sqrt {-\omega ^{2}}}\Rightarrow m=\pm \mathrm {i} \omega$

因此，微分方程的通解可以寫成

$x=A_{1}\cos(\omega t)+A_{2}\sin(\omega t)\,$，或等效地，$x=A_{3}\cos(\omega t+\varepsilon )\,$。

為了求解常數對 $\{A_{1},A_{2}\}$ 或 $\{A_{3},\varepsilon \}$，我們需要一對描述 SHM 的初始條件。

如果粒子從最大位移 $x=a$靜止開始，那麼我們將 $x=a$ 和 ${\frac {dx}{dt}}=0$ 代入到 $t=0$，得到 $A_{1}=a$，$A_{2}=0$ 和 $A_{3}=a$，$\varepsilon =0$。解變為 $x=a\cos(\omega t)\,$。

另一方面，如果振盪從最小位移開始，那麼我們將得到 $x=a\sin(\omega t)=a\cos \left(\omega t-{\frac {\pi }{2}}\right)\,$。

一般來說，我們有

$x=a\cos(\omega t+\varepsilon )\,$

其中常數 $\varepsilon$ 取決於振盪器的起始位置。

這些方程式表明 $\omega$ 僅僅是與簡諧運動相關的 恆定角速度（或角頻率）。下圖說明了簡諧運動和 勻速圓周運動（角速度為 $\omega$）之間的關係。簡諧振子的位移 $x$ 實際上只是執行勻速圓周運動的粒子的 $x$ 座標。因此，我們可以將簡諧運動視為勻速圓周運動在圓的直徑上的投影。

簡諧振子每經過兩次端點間的距離（即距離 $4a$）就完成 一次振盪。這對應於勻速圓周運動中 一次旋轉。因此，簡諧運動的 振盪週期 由下式給出

$T={\frac {2\pi }{\omega }}\,$

示例：彈性弦上的質量

我們希望確定懸掛在輕質（即無質量）彈性弦上的質量是否會表現出簡諧運動。

考慮一根 自然長度 為 $l$，彈性模量 為 $\lambda$ 的輕質彈性弦，從固定點 O 垂直懸掛。弦的另一端連線到 質量 為 $m$ 的粒子。

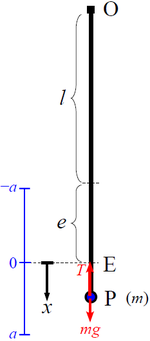
設點 E 表示粒子的 平衡位置。在 E 點，粒子處於靜止狀態（即作用在其上的合力為零）。設 $e$ 表示粒子位於 E 點時弦的伸長量。考慮作用在粒子上的豎直力，得到

${\frac {\lambda }{l}}e=mg\Rightarrow e={\frac {mgl}{\lambda }}$.

質量的位移 $x$ 始終從平衡位置 E 測量，因為這是 ${\ddot {x}}=0$ 且因此合力 $F=0$ 的點。

假設質量經歷了一個小的位移 $x$。應用 牛頓第二定律，得到

	$mg-T$	$=m{\ddot {x}}$
$\Rightarrow$	$mg-{\frac {\lambda }{l}}(e+x)$	$=m{\ddot {x}}$
$\Rightarrow$	$mg-{\frac {\lambda }{l}}e-{\frac {\lambda }{l}}x$	$=m{\ddot {x}}$
$\Rightarrow$	$-{\frac {\lambda }{l}}x$	$=m{\ddot {x}}$ (since $mg={\frac {\lambda }{l}}e$)
$\Rightarrow$	${\ddot {x}}$	$=-{\frac {\lambda }{ml}}x$

這是簡諧運動的定義運動方程，其中 $\omega ^{2}={\frac {\lambda }{ml}}$。請注意，只有當繩子保持繃緊時，即 $a<e$，粒子才能進行簡諧運動。

總結

您需要知道以下公式，因為考試中不會提供這些公式。

公式	描述
${\ddot {x}}=-\omega ^{2}x$	簡諧運動的定義運動方程（用加速度和位移表示）
$v^{2}=\omega ^{2}\left(a^{2}-x^{2}\right)$	簡諧運動的運動方程，用速度、振幅和位移表示
$x=a\cos(\omega t+\varepsilon )\$	簡諧運動的運動方程，用位移、振幅和時間表示
$T={\frac {2\pi }{\omega }}$	簡諧運動的振盪週期