A-level 物理 (進階物理)/圖

有兩種型別的運動圖，你需要能夠使用和理解：距離-時間圖和速度-時間圖。

距離-時間圖

一個物體以恆定速度運動 6 秒，停止 5 秒，然後在接下來的 7 秒內返回到其初始位置，在返回旅程的中間部分移動得更慢。

距離-時間圖繪製物體離開某一點的距離，以時間為橫軸，距離為縱軸。你需要能夠使用和理解幾種型別的運動圖：距離-時間圖、位置-時間圖和速度-時間圖。

位置-時間圖或位移-時間圖

距離-時間圖可以告訴你速度，但速度永遠不會是負數，所以距離-時間圖中只能有正斜率。位置-時間圖顯示位移，有方向，你可以從中計算速度。如果我們把位置-時間圖上的直線想象成一個函式 f(t)，給出 s = f(t) 的方程，我們可以對其進行微分，得到

${\frac {ds}{dt}}=f'(t)$,

其中 s 是位移，t 是時間。透過在任何給定的時間 t 找到 f'(t)，我們可以找到距離相對於 t 的變化率。這就是直線的斜率。正斜率意味著距離在增加，負斜率意味著距離在減少。斜率為 0 意味著物體靜止。物體的速度是其位移的變化率，這與距離-時間圖上直線的斜率相同。但這不一定與物體的平均速度 v 相同

$v={\frac {s}{t}}$

在這裡，t 和 s 是特定時間段內位移和時間的總變化 - 它們不能告訴你任何給定時間點到底發生了什麼。

速度-時間圖

一個物體加速 6 秒，撞到某個物體，加速 5 秒，然後在剩下的 6.5 秒旅程中減速到停止。

速度-時間圖繪製物體相對於某一點的速度，以時間為橫軸，速度為縱軸。我們已經知道速度是距離函式的斜率（導數）。由於積分是微分的逆過程，如果我們有速度-時間圖，並且想要知道物體在兩個時間點之間的距離，我們可以找到這兩個時間點之間圖下的面積。一般來說

如果 $v=f(t)\,$

$s=\int _{t_{1}}^{t_{2}}f(t)\,dt$

其中 v 是速度（單位為 ms⁻¹），t 是時間（單位為 s），s 是物體在兩個時間點 t₁ 和 t₂ 之間的距離（單位為 m）。

此外，透過微分，我們知道 v = f(t) 的斜率（或導數）等於物體在任何給定時間點的加速度（單位為 ms⁻²），因為

$a={\frac {dv}{dt}}$

問題

1. 在以下距離-時間圖中，物體運動開始後 4 秒的速度是多少？

2a) 描述這個人的運動。

2b) 12 秒時的速度是多少？

3. 在以下速度-時間圖中，物體在 7 秒到 9 秒之間運動了多少距離？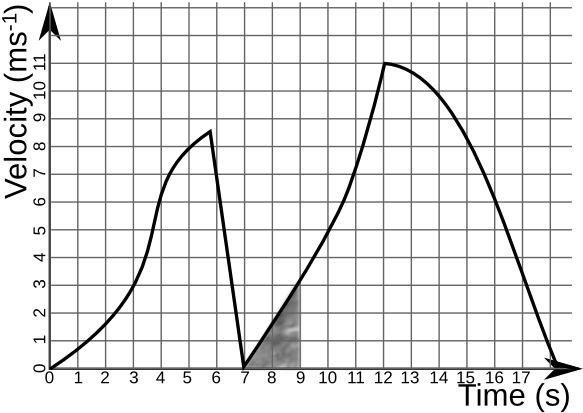

4. 物體在 8 秒時的加速度是多少？

5. 一輛汽車以 10ms⁻¹ 的速度在直線上行駛 5 分鐘，然後在接下來的 4 分鐘內以恆定速度返回其初始位置。繪製一張距離-時間圖，顯示汽車從其初始位置行駛的距離。

6. 繪製上述情況的速度-時間圖。

以下問題比你將要遇到的任何問題都更難，但還是試一試吧

7. 小球的速度與它被丟擲後的時間有關，方程為 $v=30-9.8t\,$。小球在 2 秒後運動了多遠？

解答