A-level 物理（進階物理）/簡諧運動

當作用於物體的力與物體的位移成正比且方向相反時，就會發生簡諧運動。例如，彈簧上的質量和擺錘，它們會反覆地來回“彈跳”。在數學上，這可以寫成

$F=-kx$ ,

其中 F 是力，x 是位移，k 是一個正常數。這與胡克定律完全相同，胡克定律指出，彈簧末端的物體上的力 F 等於 -kx，其中 k 是彈簧常數。由於 F = ma，而加速度是位移對時間 t 的二階導數

$m{\frac {d^{2}x}{dt^{2}}}=-kx$

${\frac {d^{2}x}{dt^{2}}}={\frac {-kx}{m}}$

這個二階微分方程的解是

$x=A\cos {\omega t}$ ,

其中 A 是最大位移，ω 是物體的“角速度”。推導過程見這裡，因為對於那些以前沒有接觸過複數的人來說，它看起來會非常可怕。需要注意的是，這個解在給定不同的起始條件後，會變成

$x=A\sin {\omega t}$ ,

角速度

圓周運動中的角速度是角變化率。它以弧度/秒為單位。由於 2π 弧度相當於週期 T 內的一次完整旋轉

$\omega ={\frac {2\pi }{T}}=2\pi f$

如果我們將它代入簡諧運動中位移的方程

$x=A\cos {2\pi ft}$

方程中包含角速度的原因是，簡諧運動與圓周運動非常相似。如果你從側面觀察一個物體繞圓圈運動，它看起來就像簡諧運動。我們已經注意到，彈簧上的質量會發生簡諧運動。下圖顯示了圓周運動和簡諧運動之間的相似性

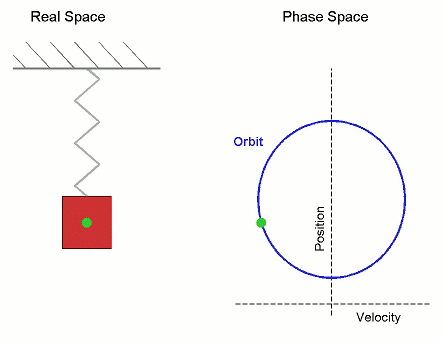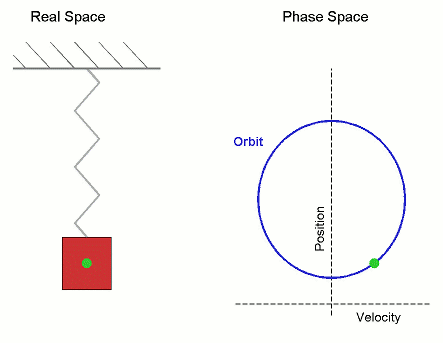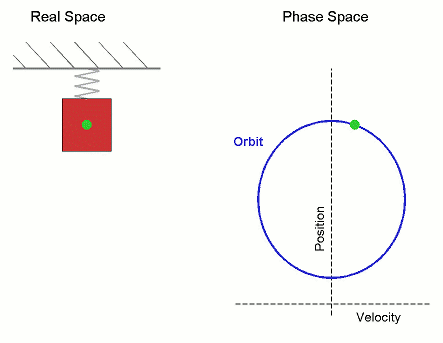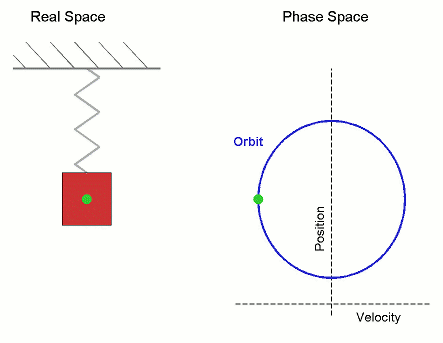
振盪的週期是指重複運動模式一次所需的時間。一般來說

$T={\frac {2\pi }{\omega }}$

但是，根據振盪的型別，ω 的值會發生變化。對於彈簧上的質量

$\omega ={\sqrt {\frac {k}{m}}}$

對於擺錘

$\omega ={\sqrt {\frac {g}{l}}}$ ,

其中 g 是重力場強，l 是繩子的長度。透過代入，我們可以得到以下表格

振盪型別	彈簧	擺錘
角速度	${\sqrt {\frac {k}{m}}}$	${\sqrt {\frac {g}{l}}}$
週期	$2\pi {\sqrt {\frac {m}{k}}}$	$2\pi {\sqrt {\frac {l}{g}}}$

簡諧振子的位移是

$x=A\cos {\omega t}$

速度是位移變化率，所以

$v={\frac {dx}{dt}}=-A\omega \sin {\omega t}$

加速度是速度變化率，所以

$a={\frac {dv}{dt}}={\frac {d^{2}x}{dt^{2}}}=-A\omega ^{2}cos{\omega t}=-\omega ^{2}x$

1. 一個 10 牛頓的重物使彈簧伸長 5 釐米。再新增一個 10 牛頓的重物，彈簧又伸長了 5 釐米。彈簧的彈性係數是多少？

2. 將彈簧帶到外太空，用兩個重物將其拉伸 10 釐米。它的振動週期是多少？

3. 1 秒後，彈簧上作用著什麼力？力的方向是什麼？

4. 一個擺的振動頻率是 0.5 赫茲。擺的長度是多少？

5. 下圖顯示了簡諧振子的位移。繪製出它的速度、動量、加速度和作用在其上的力的圖。

6. 只有當擺的振動角度很小時，它才能被建模為簡諧振子。這是為什麼？