A-level 物理（高階物理學）/楊氏雙縫

您應該熟悉以下概念：當光線透過狹縫時，它會發生衍射（從狹縫向外以弧形傳播）。衍射量隨著狹縫寬度越接近光波長而增加。考慮右側的動畫。來自光源的光線被引導透過兩個狹縫。它在這兩個狹縫處都發生了衍射，因此它以兩組弧形傳播。

現在，將波的疊加應用於這種情況。在某些點，波的波峰（或波谷）會重合，形成相長干涉。如果這發生在螢幕上，那麼將可見一條明亮的“條紋”。另一方面，如果發生相消干涉（波峰與波谷重合），那麼在螢幕上的那個點將不會有光線可見。

計算條紋出現的角度

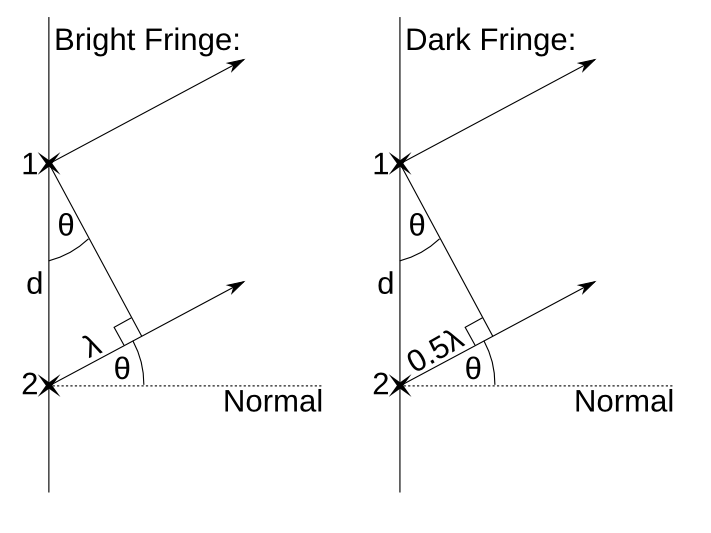
如果我們想計算亮條紋的位置，我們知道，在這個點上，波必須同相。或者，在暗條紋處，波必須反相。如果我們令波長等於 λ，光束相對於法線的角度等於 θ，狹縫之間的距離等於 d，我們可以形成兩個三角形，一個用於亮條紋，另一個用於暗條紋（標有 1 和 2 的十字是狹縫）。

標有 λ 的邊的長度被稱為路程差。對於亮條紋，從上面的幾何形狀，我們知道

$\sin {\theta }={\frac {\lambda }{d}}$

所以

$\lambda =d\sin {\theta }\,$

但是，亮條紋不只在標有 λ 的邊等於 1 個波長時出現：它可以等於多個波長，只要它是完整的波長即可。因此

$n\lambda =d\sin {\theta }\,$,

其中 n 是任何整數。

現在考慮右手三角形，它適用於暗條紋。我們知道，在這種情況下

$\sin {\theta }={\frac {0.5\lambda }{d}}$

$0.5\lambda =d\sin {\theta }\,$

我們也可以對此進行推廣，適用於任何暗條紋。但是，如果將 0.5λ 乘以偶數，那麼我們將得到一個完整的波長，這將導致亮條紋，而不是暗條紋。所以，n 在以下公式中必須是奇數

$0.5n\lambda =d\sin {\theta }\,$

$n\lambda =2d\sin {\theta }\,$

計算角度對應的螢幕上的距離

在這一點上，我們必須進行一些略微不嚴謹的數學運算。在下面的圖中，p 是路程差，L 是從狹縫到螢幕的距離，x 是從條紋到法線的垂直距離。

在這裡，有必要將從狹縫到條紋的距離近似為從狹縫到螢幕的垂直距離。這是可以接受的，前提是 θ 很小，它將是，因為亮條紋隨著它們離狹縫對面的螢幕上的點越來越遠而變暗。因此

$\sin {\theta }={\frac {x}{L}}$

如果我們將此代入路程差 p 的方程

$p=d\sin {\theta }={\frac {dx}{L}}$

所以，在亮條紋處

$n\lambda ={\frac {dx}{L}}$，其中 n 為整數。

在暗條紋處

$n\lambda ={\frac {2dx}{L}}$，其中 n 為奇數。

你可能已經注意到 $x$ 不完全等於條紋到法線的距離，它與法線的距離相差 ${\frac {d}{2}}$。但是，在衍射光柵中，狹縫之間的距離與 $x$ 相比可以忽略不計，因此可以忽略。

衍射光柵

衍射光柵由許多間距為 d 的狹縫組成。與雙縫一樣，當 $n\lambda =d\sin {\theta }$ 時，所有狹縫的峰值或谷值重合，你會看到亮條紋。事情會變得稍微複雜一些，因為所有狹縫都有不同的位置，它們會疊加在一起，但你只需要知道衍射光柵會形成明暗條紋，並且這些條紋的方程與雙縫的方程相同。

問題

1. 在雙縫實驗中，兩縫間距為 0.03 米，在法線方向 10° 處觀察到亮條紋。使用的是哪種電磁輻射？

2. 波長為 500 奈米的的光線透過兩個間距為 0.05 米的狹縫。前三個暗條紋到法線的角度是多少？

3. 波長為 1 奈米的 X 射線照射到狹縫間距為 50 微米的衍射光柵上。螢幕距離光柵 1.5 米。前三個亮條紋距離法線在螢幕上的交點多遠？

解答