考慮一個從靜止狀態以恆定加速度 1g 加速的火箭。考慮到相對論效應,我們實際上指的是什麼?顯然,火箭不能以恆定速率增加速度(對於保持靜止的人來說),因為它最終會超過光速。實際上發生的是,火箭以指數方式接近光速,如下所示。
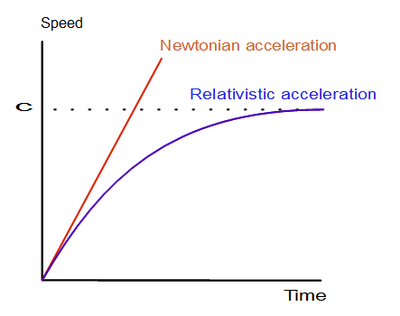 相對論加速度和牛頓加速度
相對論加速度和牛頓加速度
那麼我們指的是恆定加速度什麼呢?好吧,從船上宇航員的角度來看,我們指的是他們體驗到一個恆定的模擬重力場,該重力場是由持續燃燒的火箭發動機的穩定推力產生的,這與地球上的 1g 感受完全一樣。對他們來說,宇宙飛船永遠處於靜止狀態,但船外的宇宙看起來以越來越快的速度經過,就像上面的插圖一樣。
現在,我們似乎需要在這裡使用廣義相對論的概念,但實際上沒有必要。我們只需要仔細定義我們指的是這種加速度的哪種型別。在牛頓世界中,如果以速度 v 運動的物體以加速度 a 加速一小段時間 δt,則最終速度由下式給出

|
然而,在相對論世界中,我們必須使用相對論速度疊加公式(見附錄 *),即

|
這導致

|

|
消去二階項,我們得到

|

|
現在我們所要做的就是對這個表示式進行積分,以找出 v 如何隨 t 變化。首先分離變數

|

|
現在積分

|
幸運的是,這是一個標準積分,我的數學書告訴我它是

|
(由於 v 在 t = 0 時為 0,因此沒有積分常數)。一些簡單的操作可以讓我們得到第一個結果

|
注意這裡提到的時間 t 是 proper time 的積分,也就是行程時間 - 也就是飛船上的乘客所經歷的時間。所以這個公式告訴你經過時間 t 後你的速度會是多少。
接下來,我們想知道在這段時間內你能走多遠。為了做到這一點,我們必須考慮到越快,你經過的距離就越縮短!在牛頓世界中,在短時間 δt 內以速度 v 行駛的距離 δs 為

|
但在相對論世界中,你實際上走得更遠,因為飛船外所有的距離都因 γ 倍的長度收縮,所以

|

|
將我們經過時間 t 後飛船速度的公式代入,我們得到

|

|
對這個表示式進行積分,得到

|
這次我們不能忽略積分常數,因為當 t = 0 時,s = 0,但 cosh(0) 為 1 而不是零。因此,最終結果為

|
我們想了解的第三件事是,我們回來的時候我們的朋友會多大歲數!好吧,對於我們以速度 v 行駛的每一秒,留在地球上的朋友會老 γ 秒,即

|

|

|
由此,我們得到

|
(積分常數為零,因為 sinh(0) = 0,正如預期的那樣)
我發現 1g 火箭問題的解擁有如此簡單而優雅的答案,尤其是在我們使用年和光年進行計算時,這一點特別令人滿意。在這些單位中,a 和 c 都等於 1。如果我們考慮一個往返行程,該行程需要 T 年(以飛船上的時間測量),那麼往程將包含兩個階段,加速階段持續 T/4 年,減速階段同樣長。返程也一樣。
達到的最大速度將是

|
你將到達的距離是

|
當你回來時,你剛出生的小兒子的年齡將是

|
為了讓你瞭解這些表示式在實際應用中的樣子,這裡有一個結果表
| 旅程時間 (年) |
最大速度 (% of c) |
距離 (光年) |
兒子年齡 (年) |
| 0 |
0 |
0 |
0
|
| 1 |
24 |
0.1 |
1
|
| 2 |
46 |
0.3 |
2
|
| 3 |
64 |
0.6 |
3
|
| 4 |
76 |
1.1 |
5
|
| 5 |
85 |
2 |
6
|
| 6 |
91 |
3 |
9
|
| 7 |
94 |
4 |
11
|
| 8 |
96 |
6 |
15
|
| 9 |
98 |
8 |
19
|
| 10 |
99 |
10 |
24
|
值得注意的是,理論上往返一顆距離地球10光年的恆星只需要10年的宇航員時間 (而地球上已經過去了24年)。如果你準備旅行20年、30年或40年,你可以分別到達距離地球150光年、1800光年和22000光年的恆星 (這相當於銀河系四分之一的距離!) 如果你不介意不回家,你可以在僅僅47年內到達已知宇宙的邊緣 (不過,當你到達那裡時,宇宙是否還存在就是另一個問題了!)
回到引言...
回到頂部...


























