所有正常的物質體,如固體和氣體,都服從質量連續性方程。在直角座標系中,可以使用多種符號方法表示它。
∂ ρ ∂ t + ∂ ( ρ u i ) ∂ x i = ∂ ρ ∂ t + ∇ ∙ ρ V = ∂ ρ ∂ t + ∂ ( ρ u x ) ∂ x + ∂ ( ρ u y ) ∂ y + ∂ ( ρ u z ) ∂ z = 0 {\displaystyle {\frac {\partial \rho }{\partial t}}+{\frac {\partial (\rho {{u}_{i}})}{\partial {{x}_{i}}}}={\frac {\partial \rho }{\partial t}}+\nabla \bullet \rho V={\frac {\partial \rho }{\partial t}}+{\frac {\partial (\rho {{u}_{x}})}{\partial x}}+{\frac {\partial (\rho {{u}_{y}})}{\partial y}}+{\frac {\partial (\rho {{u}_{z}})}{\partial z}}=0}
本質上,方程的右側解釋了小體積內的質量流入/流出率。如果總和為零,則密度不會隨時間變化。該物質被認為是不可壓縮的 ,訊號傳播速度是無限的。任何區域性動作都會立即傳遞到所有其他位置。所有材料都具有一定程度的可壓縮性 ,因此密度會隨時間變化,並且具有有限的傳播速度。任何區域性動作都需要一定的時間才能到達遠端位置,因此所有描述性方程都必須包含一個時間延遲因子。由於這裡關注的是航空聲學,因此傳播速度由與氣體特性相關的幾個因素決定。氣體的運動受上述方程以及動量方程的控制,該方程將流體響應與幾種力聯絡起來;該方程是非線性的。
∂ ( ρ u i ) ∂ t + ∂ ( ρ u i u j ) ∂ x j = ∂ p ∂ x j + υ ∂ u i ∂ x j {\displaystyle {\begin{aligned}&{\frac {\partial (\rho {{u}_{i}})}{\partial t}}+{\frac {\partial (\rho {{u}_{i}}{{u}_{j}})}{\partial {{x}_{j}}}}={\frac {\partial p}{\partial {{x}_{j}}}}+\upsilon {\frac {\partial {{u}_{i}}}{\partial {{x}_{j}}}}\\&\\\end{aligned}}}
如果做出一些簡化的假設,則可以從中提取線性聲波方程。
∂ 2 s ∂ x 2 − 1 c 0 2 ∂ 2 s ∂ t 2 = 0 s = ρ − ρ 0 ρ 0 {\displaystyle {\begin{aligned}&{\frac {{{\partial }^{2}}s}{\partial {{x}^{2}}}}-{\frac {1}{c_{0}^{2}}}{\frac {{{\partial }^{2}}s}{\partial {{t}^{2}}}}=0\\&s={\frac {\rho -{{\rho }_{0}}}{{\rho }_{0}}}\\\end{aligned}}}
這裡用密度變化來表示,並與一個恆定的流體密度和一個恆定的傳播速度(稱為聲速)相關聯;這些用下標 0 表示。該速度基於所有物理變化都很小。如果不是這樣,傳播速度會更高,並導致眾所周知的衝擊波現象。這裡的發展將透過一個邊界將區域隔開,在這個邊界之外,波動方程適用。這個方程用於波動傳播,不包含源項。Lighthill 的開創性工作 [ 1] T i j {\displaystyle {{T}_{ij}}}
∂ 2 ρ ∂ t 2 − c 0 2 ∂ 2 ρ ∂ x i 2 = ∂ 2 T i j ∂ x i ∂ x j T i j = ρ u i u j − σ i j + ( p − c 0 2 ρ ) δ i j {\displaystyle {\begin{aligned}&{\frac {{{\partial }^{2}}\rho }{\partial {{t}^{2}}}}-c_{0}^{2}{\frac {{{\partial }^{2}}\rho }{\partial x_{i}^{2}}}={\frac {{{\partial }^{2}}{{T}_{ij}}}{\partial {{x}_{i}}\partial {{x}_{j}}}}\\&{{T}_{ij}}=\rho {{u}_{i}}{{u}_{j}}-{{\sigma }_{ij}}+(p-c_{0}^{2}\rho ){{\delta }_{ij}}\\\end{aligned}}}
有許多文章展示了該方程的一般解 氣動聲學 [ 2] [ 3] [ 4]
c 0 2 ( ρ − ρ 0 ) = ∂ 2 ∂ x i x j ∫ V [ T i j ] d 3 y 4 π r − ∂ ∂ x i ∮ S [ ρ u i u j + p i j ′ ] d S j ( y ) 4 π r + ∂ ∂ t ∮ S [ ρ u j ] d S j ( y ) 4 π r {\displaystyle c_{0}^{2}(\rho -{{\rho }_{0}})={\frac {{\partial }^{2}}{\partial {{x}_{i}}{{x}_{j}}}}\int \limits _{V}{\left[{{T}_{ij}}\right]}{\frac {{{d}^{3}}y}{4\pi r}}-{\frac {\partial }{\partial {{x}_{i}}}}\oint \limits _{S}{\left[\rho {{u}_{i}}{{u}_{j}}+p_{ij}^{'}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}+{\frac {\partial }{\partial t}}\oint \limits _{S}{\left[\rho {{u}_{j}}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}}
變數 r 是聲源區域 y 到遠場位置 x 的距離。方括號表示與該位置相關的時間延遲因子。第一項指的是整個應力張量 T i j {\displaystyle {{T}_{ij}}} ϕ {\displaystyle \phi }
假設我們在點 x 0 {\displaystyle \mathbf {x} _{0}}
1 c 0 2 ∂ 2 ϕ ∂ t 2 − ∇ 2 ϕ = − q ( t ) δ ( x − x 0 ) {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}\phi }{\partial \,t^{2}}}-\nabla ^{2}\phi =-q(t)\delta (\mathbf {x-x_{0}} )}
使用之前介紹的自由空間格林函式 [1] ,速度勢將為
ϕ ( x , t ) = 1 4 π ∫ − ∞ ∞ q ( y , t − | x − y | / c 0 ) δ ( y − x 0 ) | x − y | d 3 y d τ = − q ( t − | x − x 0 | / c 0 ) 4 π | x − x 0 | {\displaystyle \phi (x,t)={\frac {1}{4\pi }}\int _{-\infty }^{\infty }{\frac {q(\mathbf {y} ,t-|\mathbf {x} -\mathbf {y} |/c_{0})\delta (\mathbf {y-x_{0}} )}{|\mathbf {x} -\mathbf {y} |}}d^{3}\,\mathbf {y} d\tau =-{\frac {q(t-|\mathbf {x-x_{0}} |/c_{0})}{4\pi \,|\mathbf {x-x_{0}} |}}}
如果聲源位於原點,則上述解看起來像下面的圖片。正如你所看到的,這種型別的聲源產生對稱的球面波。這種全方向聲源被稱為 **單極子**。
上述一般理論包含一個描述導致聲場的運動的源項。它可以是單個聲源,也可以是具有已知特性的聲源分佈(利希特)。下面,聲源被視為黑盒子,被封閉在一個球形邊界內,在這個邊界之外聲波方程是有效的。由此,從聲學介質中的運動推匯出聲源的性質。在這種特定情況下,我們只關心與單個單極子聲源相關的球面對稱聲學運動。這個波動方程可以用以下形式描述
∂ ∂ r 2 ( r ϕ ) − 1 c 0 2 ∂ ∂ t 2 ( r ϕ ) = 0 ϕ ( r , t ) = Q 4 π r F ( t − r c 0 ) p ( r , t ) = ρ 0 ∂ ϕ ∂ t {\displaystyle {\begin{aligned}&{\frac {\partial }{\partial {{r}^{2}}}}\left(r\phi \right)-{\frac {1}{c_{0}^{2}}}{\frac {\partial }{\partial {{t}^{2}}}}\left(r\phi \right)=0\\&\phi \left(r,t\right)={\frac {Q}{4\pi r}}F\left(t-{\frac {r}{{c}_{0}}}\right)\\&p\left(r,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&\\\end{aligned}}}
符號 φ 被稱為速度勢 ,從中可以推匯出大多數物理變數,例如壓力或速度。字母 F 代表任意函式。對維度的分析表明 Q 的維度是 L 3 / T {\displaystyle {{L}^{3}}/T} W 可以用基本的方式表示為
W = 1 4 π Z 0 ( ∂ M ∂ t ) 2 ¯ {\displaystyle W={\frac {1}{4\pi {{Z}_{0}}}}{\overline {{\left({\frac {\partial M}{\partial t}}\right)}^{2}}}}
Z0 是聲波傳播介質的特徵阻抗 。單極子的聲功率可以解釋為質量流量率 M 隨時間變化率的均方 。這種關係適用於任何波動流量,無論隨機還是週期性。最感興趣的是以規定頻率的週期性運動。它由弧度頻率 ω=2πf 描述,其中 f 是以赫茲為單位的頻率。通常會為點 單極子推匯出關係式,但如果忽略源函式,則當接近源點時,解會發散。如果描述了具有有限半徑 a 的單極子(脈動球體),這並不是一個障礙。此情況下,兩個有用的關係是
u ( a , t ) = u a e i ω t Q = 4 π a 2 u a e i ω t {\displaystyle {\begin{array}{*{35}{l}}u\left(a,t\right)={{u}_{a}}{{e}^{i\omega t}}&{}\\Q=4\pi {{a}^{2}}{{u}_{a}}{{e}^{i\omega t}}&{}\\\end{array}}}
其中 a 代表球體半徑,ua 代表表面上的徑向速度。聲壓的波動方程解可以表示為
p ( r , t ) = [ 1 1 + i k a ] ( a r ) Z 0 u a e i ( ω t − k ( r − a ) ) k = ω c 0 = 2 π f c 0 = 2 π λ {\displaystyle {\begin{aligned}&p\left(r,t\right)=\left[{\frac {1}{1+ika}}\right]\left({\frac {a}{r}}\right){{Z}_{0}}{{u}_{a}}{{e}^{i\left(\omega t-k\left(r-a\right)\right)}}\\&k={\frac {\omega }{{c}_{0}}}={\frac {2\pi f}{{c}_{0}}}={\frac {2\pi }{\lambda }}\\\end{aligned}}}
單極子輻射阻抗 符號k 被稱為波數 ,儘管它具有倒數長度的量綱。當它與距離(如r )結合時,它被解釋為用波長表示的距離。方括號中的壓力項包含一個複數變數。這是由於兩種運動:反應運動和阻尼運動。反應運動可以認為是不可壓縮的;壓力與速度正交,因此對介質不做功。阻尼運動代表對介質做功並向源輻射能量的壓縮運動。大多數聲音測量都是在距離聲源足夠遠的距離處進行的,因此只測量阻尼壓力或聲壓。該距離稱為遠場 ,而反應運動佔主導的距離稱為近場 。這兩個場之間的邊界隨著聲源強度的增加而增加,隨著頻率的增加而減小。壓力方程中方括號中的項由兩個部分組成,即單極子看到的阻尼R 和反應X 輻射阻抗 。下面的兩個方程式是它們的表示式。右側的圖形顯示了兩種阻抗隨無量綱頻率的變化。在波長非常接近聲源(低頻)的情況下,大部分運動都是不可壓縮的,只有很少一部分輸入能量作為聲音輻射出去。揚聲器設計者在這些頻率下提高聲源強度,以使整體頻率響應平坦。在較高頻率下,單極子非常有效地輻射聲音。對於單個頻率的有限單極子,聲功率可以用簡單的方式表示
A 是半徑為a 的球體的表面積,R 是球體表面上的阻尼輻射阻抗。
單極子方向性 當單極子位於硬反射平面之上距離為h的地方時,會在表面下方相同的距離處出現一個映象源。聲功率表達式必須考慮與反射相關的時延。該方程為
W = 2 A u a 2 R [ 1 + sin ( 2 k h ) 2 k h ] {\displaystyle W=2Au_{a}^{2}R\left[1+{\frac {\sin(2kh)}{2kh}}\right]}
附加項解釋了相長/相消干涉效應。當距離表面接近零時,聲功率將增加4倍(6 dB)。右側的圖形展示了干涉效應的一個例子;該圖形顯示了平面之上右象限中的聲壓級。一個單極子位於硬反射表面上方 10 英寸處,以 500 Hz 的頻率輻射。相消干涉發生在距原點約 45 度的地方。藍色弧線代表均勻單極場。在更一般的情況下,有兩個單極子彼此靠近。第二個聲源的輸出和相位可能與第一個聲源不同。一個有趣的情況是,每個聲源的尺寸和頻率都相同。對於這種情況,聲功率方程變為
W = A u 1 2 R [ 1 + ( u 2 2 u 1 2 ) + 2 u 2 u 1 sin ( 2 k h ) 2 k h cos δ ] {\displaystyle W=Au_{1}^{2}R\left[1+\left({\frac {u_{2}^{2}}{u_{1}^{2}}}\right)+{\frac {2{{u}_{2}}}{{u}_{1}}}{\frac {\sin(2kh)}{2kh}}\cos \delta \right]}
單極子干涉 燃燒單極子 脈衝噴氣發動機噪聲 符號u1 和 u2 代表兩個聲源的表面速度,字母 δ 代表兩者之間的相位差。右圖顯示了兩個單極子在 1000 Hz 頻率下輻射,相距 72 釐米,相位差為 180 度的組合聲壓級的示例。請注意,由於相位相反,它們之間平面的聲級被最小化。
現實世界中很少有聲源能很好地近似於理論上的單極子。一個例子是迄今為止存在過的最大的單極子。它是在蘇聯新地島上引爆的 5700 萬噸氫彈。 [ 5] 單極子類 。與理論單極子的相似之處在於,有一個可變質量流量產生聲場。不同之處在於,固體邊界是聲源的組成部分,而不是僅僅在附近。一個例子是平面表面上的活塞;該理論已被研究出來。 [ 6] [ 7]
還有一類單極子類聲源被稱為氣動哨聲。 [ 8]
比較同一型別聲源的不同操作模式和尺寸時,幾何相似性和動態相似性非常重要。幾何形狀由尺寸L 描述,動力學由速度U 描述。如果正確選擇這些值,它們將成為裝置的特徵。它們可用於確定如果裝置的尺寸或速度發生變化,聲音功率的變化。下面的第一個方程是點單極子在離散頻率下的方程。體積流量項可以用無量綱版本替換,頻率可以用無量綱斯特羅哈爾數替換。該數字是在研究圓柱體上的渦流脫落時由文森茨·斯特羅哈爾提出的。他發現它在一定範圍內流速(接近 0.2)是相對恆定的。斯特羅哈爾數現在可以透過使質量連續性方程無量綱直接推匯出來。如果將這兩個無量綱值代入聲音功率方程,則得到最後一個方程。對於許多聲源來說,這兩個無量綱引數都相對恆定,因此聲音功率隨著特徵速度的四次方和特徵長度的二次方而增加。 [ 9]
汽車聲級 W = k 2 Z 0 Q 2 4 π Q ^ = Q U L 2 S = f L U W = π ρ 0 c 0 Q ^ 2 S 2 U 4 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{2}}{{Z}_{0}}{{Q}^{2}}}{4\pi }}\\&{\widehat {Q}}={\frac {Q}{U{{L}^{2}}}}\\&S={\frac {fL}{U}}\\&W={\frac {\pi {{\rho }_{0}}}{{c}_{0}}}{{\widehat {Q}}^{2}}{{S}^{2}}{{U}^{4}}{{L}^{2}}\\\end{aligned}}}
汽車聲譜 後一個方程適用性的一個很好的例子是機動車聲音。右側的上面圖顯示了從各種汽車在幾個速度下在 50 英尺處測量的聲壓級。[ 10] U 4 {\displaystyle {{U}^{4}}} [ 11]
偶極子是波浪方程中出現的一個聲源,表示為
1 c 0 2 ∂ 2 p ∂ t 2 − ∇ 2 p = ∂ ∂ x j ( f j ( t ) δ ( x − x 0 ) ) {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}p}{\partial \,t^{2}}}-\nabla ^{2}p={\frac {\partial }{\partial x_{j}}}\left(f_{j}(t)\delta (\mathbf {x-x_{0}} )\right)}
與單極子不同,偶極子方程有兩個方向,一個是來自聲源的半徑,另一個是角度。聲源外部的聲學運動方程可以用這些座標表示為
1 r 2 ∂ ∂ r ( r 2 ∂ ϕ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ϕ ∂ θ ) − 1 c 0 2 ∂ 2 ϕ ∂ t 2 = 0 p ( r , θ , t ) = ρ 0 ∂ ϕ ∂ t u r ( r , θ , t ) = − ∂ ϕ ∂ r u θ ( r , θ , t ) = − 1 r ∂ ϕ ∂ θ {\displaystyle {\begin{aligned}&{\frac {1}{{r}^{2}}}{\frac {\partial }{\partial r}}\left({{r}^{2}}{\frac {\partial \phi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \phi }{\partial \theta }}\right)-{\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}\phi }{\partial {{t}^{2}}}}=0\\&p\left(r,\theta ,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&{{u}_{r}}\left(r,\theta ,t\right)=-{\frac {\partial \phi }{\partial r}}\\&{{u}_{\theta }}\left(r,\theta ,t\right)=-{\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}\\\end{aligned}}}
波動方程的外向解是
ϕ ( r , θ , t ) = Q 4 π 1 + i k r r 2 cos θ e i ( ω t − k r ) {\displaystyle \phi \left(r,\theta ,t\right)={\frac {Q}{4\pi }}{\frac {1+ikr}{{r}^{2}}}\cos \theta {{e}^{i\left(\omega t-kr\right)}}}
這個結果可以透過在特定方向上對單極子速度勢進行微分得到。
ϕ ( r , θ , t ) = ∂ ∂ r ( Q m 4 π r e i ( ω t − k r ) ) ∗ ∂ r ∂ z = Q d 4 π 1 + i k r r 2 cos θ e i ( ω t − k r ) {\displaystyle \phi (r,\theta ,t)={\frac {\partial }{\partial r}}\left({\frac {{Q}_{m}}{4\pi r}}{{e}^{i(\omega t-kr)}}\right)*{\frac {\partial r}{\partial z}}={\frac {{Q}_{d}}{4\pi }}{\frac {1+ikr}{{r}^{2}}}\cos \theta {{e}^{i(\omega t-kr)}}}
從某種意義上說,偶極子是兩個在特定方向上對齊的合併單極子。在這種情況下,Q 的維數是 L 4 ╱ T {\displaystyle {}^{{L}^{4}}\!\!\diagup \!\!{}_{T}\;} F 與 Q 變數的關係為 Q = i 3 F z k Z 0 {\displaystyle Q={\frac {i3{{F}_{z}}}{k{{Z}_{0}}}}}
ϕ ( r , θ , t ) = 3 F z 4 π k Z 0 [ 1 + i k r r 2 ] cos θ e i ( ω t − k r ) {\displaystyle \phi (r,\theta ,t)={\frac {3{{F}_{z}}}{4\pi k{{Z}_{0}}}}\left[{\frac {1+ikr}{{r}^{2}}}\right]\cos \theta {{e}^{i(\omega t-kr)}}}
與單極子發展類似,偶極子的聲功率可以用一種基本的方式用施加的力來表示,如下所示
W = 3 4 π Z 0 c 0 2 ( ∂ F z ∂ t ) 2 ¯ {\displaystyle W={\frac {3}{4\pi {{Z}_{0}}c_{0}^{2}}}{\overline {{\left({\frac {\partial {{F}_{z}}}{\partial t}}\right)}^{2}}}}
聲功率可以解釋為施加在介質上特定方向上的力的變化率的均方 。
最感興趣的是半徑為 a 的剛性球體,它在 z 方向上以特定頻率振動(有限尺寸的偶極子)。各種場是
p ( r , θ , t ) = i 3 F z 4 π r 2 ( 1 + i k r 1 + i k a ) c o s θ e i ( ω t − k ( r − a ) ) u r ( r , θ , t ) = 3 F z 4 π k r 3 Z 0 ( 2 ( 1 + i k r ) − k 2 r 2 1 + i k a ) c o s θ e i ( ω t − k ( r − a ) ) u θ ( r , θ , t ) = − i 3 F z 4 π k r 3 Z 0 ( 1 + i k r 1 + i k a ) s i n θ e i ( ω t − k ( r − a ) ) {\displaystyle {\begin{aligned}&p\left(r,\theta ,t\right)={\frac {i3{{F}_{z}}}{4\pi {{r}^{2}}}}\left({\frac {1+ikr}{1+ika}}\right)cos\theta {{e}^{i(\omega t-k(r-a))}}\\&{{u}_{r}}\left(r,\theta ,t\right)={\frac {3{{F}_{z}}}{4\pi k{{r}^{3}}{{Z}_{0}}}}\left({\frac {2(1+ikr)-{{k}^{2}}{{r}^{2}}}{1+ika}}\right)cos\theta {{e}^{i(\omega t-k(r-a))}}\\&{{u}_{\theta }}\left(r,\theta ,t\right)={\frac {-i3{{F}_{z}}}{4\pi k{{r}^{3}}{{Z}_{0}}}}\left({\frac {1+ikr}{1+ika}}\right)sin\theta {{e}^{i(\omega t-k(r-a))}}\\\end{aligned}}}
強度有兩個分量。徑向強度具有阻性和感抗分量,而角向強度僅具有感抗分量。這表明該運動在聲場中儲存的不可壓縮能量比單極子更多。右側的圖形顯示了由此產生的指向性圖。
偶極子強度場 I r ( r , θ ) = 9 F z 2 16 π 2 Z 0 [ k 2 r 2 r 4 ( 1 + k 2 a 2 ) = + i 2 + k 2 r 2 r 4 ( 1 + k 2 a 2 ) k r ] c o s 2 θ I θ ( r , θ ) = i 9 F z 2 32 π 2 Z 0 [ 1 + k 2 r 2 r 4 ( 1 + k 2 a 2 ) k r ] s i n 2 θ {\displaystyle {\begin{aligned}&{{I}_{r}}(r,\theta )={\frac {9F_{z}^{2}}{16{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})}}=+i{\frac {2+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]co{{s}^{2}}\theta \\&{{I}_{\theta }}(r,\theta )={\frac {i9F_{z}^{2}}{32{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {1+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]sin2\theta \\\end{aligned}}}
有限偶極子的聲功率為
W = 3 F z 2 4 π a 2 Z 0 [ k 2 a 2 1 + k 2 a 2 ] {\displaystyle W={\frac {3F_{z}^{2}}{4\pi {{a}^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{a}^{2}}}{1+{{k}^{2}}{{a}^{2}}}}\right]}
有限偶極子的輻射阻抗為
偶極子阻抗 R = Z 0 k 4 a 4 4 + k 4 a 4 X = Z 0 k a ( 2 + k 2 a 2 ) 4 + k 4 a 4 {\displaystyle {\begin{aligned}&R={{Z}_{0}}{\frac {{{k}^{4}}{{a}^{4}}}{4+{{k}^{4}}{{a}^{4}}}}\\&X={{Z}_{0}}{\frac {ka(2+{{k}^{2}}{{a}^{2}})}{4+{{k}^{4}}{{a}^{4}}}}\\\end{aligned}}}
偶極子在低頻下的電抗明顯高於單極子,表明不可壓縮場中儲存了大量能量。低頻下的電阻阻抗遠低於單極子,表明這些頻率下的輻射效率低下。
當偶極子距離硬反射面h 時,映象源出現在表面下方相同的距離。與單極子不同,力的方向向量以及與反射相關的時延也必須考慮在內。均方聲壓方程為
p p ∗ = 9 F z 2 16 π 2 ( 1 + k 2 a 2 ) [ ( 1 + k 2 r 1 2 ) r 1 4 cos 2 α 1 + ( 1 + k 2 r 2 2 ) r 2 4 cos 2 α 2 + 2 cos α 1 cos α 2 r 1 2 r 2 2 [ ( 1 + k r 1 r 2 ) cos k ( r 2 − r 1 ) + k ( r 2 − r 1 ) sin k ( r 2 − r 1 ) ] ] {\displaystyle p{{p}^{*}}={\frac {9F_{z}^{2}}{16{{\pi }^{2}}(1+{{k}^{2}}{{a}^{2}})}}\left[{\frac {(1+{{k}^{2}}r_{1}^{2})}{r_{1}^{4}}}{{\cos }^{2}}{{\alpha }_{1}}+{\frac {(1+{{k}^{2}}r_{2}^{2})}{r_{2}^{4}}}{{\cos }^{2}}{{\alpha }_{2}}+{\frac {2\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}}{r_{1}^{2}r_{2}^{2}}}\left[(1+k{{r}_{1}}{{r}_{2}})\cos k({{r}_{2}}-{{r}_{1}})+k({{r}_{2}}-{{r}_{1}})\sin k({{r}_{2}}-{{r}_{1}})\right]\right]}
垂直偶極子方向性 水平偶極子方向性 由於反射力向量方向是源向量的映象,因此需要考慮兩個角度。圖中給出了這個繁瑣方程的影響示例。在第一個示例中,左側,偶極子相對於水平表面垂直定向,並在 1000 Hz 頻率下輻射。源位於表面上方 20 釐米,因此會發生相消干涉,標準偶極子方向性會發生改變。第二個圖,右側,是偶極子軸處於水平狀態時的情況;其他條件保持不變。兩個相互作用的偶極子在任意大小、頻率、角度和相位差下更一般的情況可以被公式化,但不會更有啟發性。
很少有聲源接近於理論偶極子;大多數被稱為類偶極子。相似之處在於產生的聲場。不同之處在於產生聲場的過程。在實際情況下,驅動聲場的力是由流體與固體物體相互作用產生的動量波動產生的。雖然單極子源明顯與密度變化相關,但在實際偶極子情況下,密度變化可能會被埋藏在一個可以被視為不可壓縮的流場中,以便進行分析。渦聲理論被髮展出來來處理這種情況[ 12] [ 13] [ 14] [ 15]
兩個單極子的偶極子 兩個渦流 振盪球體 一個典型的渦流例子是氣流經過圓柱體產生的風鳴聲。渦流交替地從圓柱體中脫落。左圖顯示了從圓柱體(深色圓圈)中脫落的兩個相干渦流的兩個階段。圍繞圓柱體的振盪迴圈導致產生一個類偶極聲場的力量。與理論偶極子不同,不對稱性導致垂直於流動的升力偶極子和平行於流動的阻力偶極子。正是這種現象被文森佐·斯特魯哈爾研究[ 16] [ 17] [ 18] 由於在自由流中,總渦流強度(迴圈乘以面積)不可能發生變化,因此沒有淨偶極子強度,但每個移動的渦量元素仍然會引起區域性類偶極子流動。一個關鍵的結果是,在略微可壓縮的流體中,渦量可以被認為是誘導整個流場,包括流體力學部分和聲學部分。
風鳴聲流 排氣偶極子 來自環的偶極子聲 當比較同一源型別不同操作模式和尺寸時,幾何相似性和動態相似性很重要。幾何形狀由尺寸 L 描述,動力學由速度 U 描述。如果這些值選擇得當,它們就會成為裝置的特徵。它們可以用來確定如果裝置的尺寸或速度發生變化,聲功率的變化。下面第一個方程是點偶極子在離散頻率下的方程。波動力可以用無量綱版本代替,頻率可以用無量綱斯特魯哈爾數代替。如果將這些無量綱值代入聲功率方程,則得到最後一個方程。對於許多偶極子聲源,這兩個無量綱引數都相對恆定,因此聲功率隨特徵速度的六次方和特徵長度的二次方而增加。這種關係已在許多實際聲源中得到證實。
W = 3 k 2 F z 2 4 π Z 0 F z ^ = F z ρ 0 U 2 L 2 S = f L U W = 3 π ρ 0 c 0 3 F z ^ 2 S 2 U 6 L 2 {\displaystyle {\begin{aligned}&W={\frac {3{{k}^{2}}F_{z}^{2}}{4\pi {{Z}_{0}}}}\\&{\widehat {{F}_{z}}}={\frac {{F}_{z}}{{{\rho }_{0}}{{U}^{2}}{{L}^{2}}}}\\&S={\frac {fL}{U}}\\&W={\frac {3\pi {{\rho }_{0}}}{c_{0}^{3}}}{{\widehat {{F}_{z}}}^{2}}{{S}^{2}}{{U}^{6}}{{L}^{2}}\\\end{aligned}}}
後緣噪聲 渦旋哨聲是由管口處的旋流前移產生的[ 19] [ 20] [ 21] [ 22]
四極子是涉及兩個空間導數的源分佈。
1 c 0 2 ∂ 2 p ∂ t 2 − ∇ 2 p = ∂ 2 T i j ∂ x i ∂ x j {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}p}{\partial \,t^{2}}}-\nabla ^{2}p={\frac {\partial ^{2}T_{ij}}{\partial x_{i}\partial x_{j}}}}
下方顯示了一個點橫向四極子產生的聲場。請注意最大聲級的角度。
與偶極子和單極子不同,四極子的方程具有三個方向,即從源頭的半徑和兩個角度。該方程可以用球座標表示,其中線性方程有效,如
1 r 2 ∂ ∂ r ( r 2 ∂ ϕ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ϕ ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 ϕ ∂ ψ − 1 c 0 2 ∂ ∂ r 2 ( r ϕ ) = 0 p ( r , θ , ψ , t ) = ρ 0 ∂ ϕ ∂ t u r ( r , θ , ψ , t ) = − ∂ ϕ ∂ r u θ ( r , θ , ψ , t ) = − 1 r ∂ ϕ ∂ θ u ψ ( r , θ , ψ , t ) = − 1 r sin θ ∂ ϕ ∂ ψ {\displaystyle {\begin{aligned}&{\frac {1}{{r}^{2}}}{\frac {\partial }{\partial r}}\left({{r}^{2}}{\frac {\partial \phi }{\partial r}}\right)+{\frac {1}{{{r}^{2}}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \phi }{\partial \theta }}\right)+{\frac {1}{{{r}^{2}}{{\sin }^{2}}\theta }}{\frac {{{\partial }^{2}}\phi }{\partial \psi }}-{\frac {1}{c_{0}^{2}}}{\frac {\partial }{\partial {{r}^{2}}}}\left(r\phi \right)=0\\&p\left(r,\theta ,\psi ,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&{{u}_{r}}\left(r,\theta ,\psi ,t\right)=-{\frac {\partial \phi }{\partial r}}\\&{{u}_{\theta }}\left(r,\theta ,\psi ,t\right)=-{\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}\\&{{u}_{\psi }}\left(r,\theta ,\psi ,t\right)=-{\frac {1}{r\sin \theta }}{\frac {\partial \phi }{\partial \psi }}\\\end{aligned}}}
四極子聲源 單極子是標量,偶極子是向量,而四極子是二階張量。偶極子可以被視為兩個相互異相的緊密單極子。四極子可以被視為兩個緊密偶極子,它們的力向量方向相反,或者四個單極子像右側圖中所示那樣排列。橫向四極子是力向量平行於彼此,但相互橫向的四極子。如該圖所示,橫向四極子與波動的剪下力有關。縱向四極子是力向量彼此平行,但處於同一直線上的四極子。如該圖所示,縱向四極子與拉伸力(泊松比型變形)有關。
這些可以被建模為四個單極子、兩個偶極子或兩個渦環。偶極子的力向量如上圖所示,另外兩個的流場如右側圖所示。沒有 嚴格的徑向流向量表明有效的聲波產生。雖然沒有顯示出來,但四個四十五度角的斜流的徑向分量是最大的(見上面的動畫)。因此,可以推斷出四個聲波瓣,而無需藉助數學。這種型別的四極子可以存在於具有速度梯度的流動中,特別是在湍流中。[ 23] [ 24]
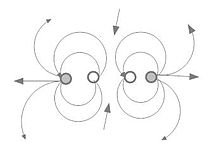
橫向四極子近流場的流體力學可以透過多種方式進行建模。左側的圖使用四個單極子來建立流場。正是這種佈置成為下一節第一個方程的基礎。中間圖使用兩個偶極子(在這裡顯示為兩個球體)來建立流場。也可以使用兩個力向量。右側圖使用兩個渦環來建立流場。橫向四極子的分佈存在於具有速度梯度的流動中,特別是在高速湍流中。
橫向四極子的單極子模型 橫向四極子的渦旋模型 橫向四極子的偶極子模型 橫向四極子是指力向量平行但相互並列,如右上角上圖所示。與不太複雜的聲源一樣,這種四極子也被認為是由四個點單極子組成,每一對縱向相隔有限距離d ,兩對橫向相隔距離D 。下面的等式是根據這些項表示聲壓的表示式。[ 25] Q 是點單極子的源函式。
p ( r , θ , ψ , t ) = Q Z 0 k 4 π r ( 4 k 2 d D ) cos θ sin θ cos ψ e i ( ω t − k r ) {\displaystyle p(r,\theta ,\psi ,t)={\frac {QZ{}_{0}k}{4\pi r}}(4{{k}^{2}}dD)\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}}
一種更具啟發性的方法是使用導數法。由於偶極子速度勢是作為單極子的導數得到的,因此橫向四極子速度勢可以透過偶極子勢的導數得到。對於橫向四極子,導數是在垂直於主偶極子軸方向的方向上取的。這種方法揭示了作用在體積上的剪下力。第一個方程式是速度勢;第二個是聲壓;第三個是均方聲壓。橫向四極子聲源可以表示為作用在體積上的剪下力時間變化率的均方的時均值 。
這種四極子的指向性如右側圖所示。三維形式很像一個拉長的氣球。
橫向四極子的指向性 φ ( r , θ , ψ , t ) = 3 F 4 π k Z 0 [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos θ sin θ cos ψ e i ( ω t − k r ) p ( r , θ , ψ , t ) = i 3 F 4 π [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos θ sin θ cos ψ e i ( ω t − k r ) p 2 ¯ ( r , θ , ψ ) = 9 ( ∂ F ∂ t ) 2 ¯ 16 π 2 [ 4 + k 4 r 4 r 6 ] cos 2 θ sin 2 cos 2 ψ {\displaystyle {\begin{aligned}&\varphi (r,\theta ,\psi ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,\psi ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta ,\psi )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{2}}\theta {{\sin }^{2}}{{\cos }^{2}}\psi \\\end{aligned}}}
其中時間導數表示作用在介質上的時變應力。
就像對單極子和偶極子所做的那樣,幾何和動態相似性可以透過使用特徵尺寸 **L** 和特徵速度 **U** 應用於四極子。下面的第一個方程使用波動應力 **τ** 的簡化形式(尺寸 F/L),用於離散頻率的點四極子。應力項可以用無量綱形式替換,頻率項可以用斯特勞哈爾數替換。如果將這些無量綱值插入聲功率方程,則得到下面的方程。這是眾所周知的歸因於萊特希爾的速率定律。由於斯特勞哈爾數被提升到高次冪,因此如果總體速度依賴性偏離該定律,也不要感到驚訝。
W = k 4 τ 2 120 π Z 0 τ ^ = τ ρ 0 U 2 L 3 S = f L U W = 2 π 3 ρ 0 15 c 0 5 S 4 τ ^ 2 U 8 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{4}}{{\tau }^{2}}}{120\pi {{Z}_{0}}}}\\&{\widehat {\tau }}={\frac {\tau }{{{\rho }_{0}}{{U}^{2}}{{L}^{3}}}}\\&S={\frac {fL}{U}}\\&W={\frac {2{{\pi }^{3}}{{\rho }_{0}}}{15c_{0}^{5}}}{{S}^{4}}{{\widehat {\tau }}^{2}}{{U}^{8}}{{L}^{2}}\\\end{aligned}}}
輻射阻抗已經計算為[ 26]
橫向四極子阻抗 R = Z 0 k 6 r 6 81 + 9 k 2 r 2 − 2 k 4 r 4 + k 6 r 6 X = Z 0 k r ( 27 + 6 k 2 r 2 + k 4 r 4 ) 81 + 9 k 2 r 2 − 2 k 4 r 4 + k 6 r 6 {\displaystyle {\begin{aligned}&R={{Z}_{0}}{\frac {{{k}^{6}}{{r}^{6}}}{81+9{{k}^{2}}{{r}^{2}}-2{{k}^{4}}{{r}^{4}}+{{k}^{6}}{{r}^{6}}}}\\&X={{Z}_{0}}{\frac {kr(27+6{{k}^{2}}{{r}^{2}}+{{k}^{4}}{{r}^{4}})}{81+9{{k}^{2}}{{r}^{2}}-2{{k}^{4}}{{r}^{4}}+{{k}^{6}}{{r}^{6}}}}\\\end{aligned}}}
右邊的圖顯示了這些阻抗的圖形表示。很明顯,低頻下的電阻輻射效率 **R** 比單極子和偶極子要差得多,而電抗 **X** 則大幾個數量級。這些頻率下的流動主要是不可壓縮的。這表明四極子聲輻射在高頻和高剪下應力(高速流動)下更有效。
理論模型的軸線在定義的方向上,因此人們期望能夠測量源的方向性。不幸的是,沒有多少高階源具有這種固定的方向性。人們最初對這些源的興趣在於噴氣發動機的噪聲,這些噪聲被確定為四極子性質。[ 27] [ 28]
同樣,這些可以建模為四個單極子,兩個偶極子或兩個渦環。偶極子的力向量如上圖所示,另外兩個的流場如右圖所示。在這種情況下,存在純徑向流動向量,表明在流動軸線上有效地產生聲音。
縱向四極子的近場流場的流體力學可以用幾種方法來建模。左邊的圖使用四個單極子來建立流場。正是這種佈置成為下一節第一個方程的基礎。中間的圖使用兩個偶極子(這裡用兩個球體表示)來建立流場。也可以使用兩個力向量。右邊的圖使用兩個渦環來建立流場。這些模型表明體積的拉伸。
縱向四極子的單極子模型 縱向四極子的渦旋模型 縱向四極子的偶極子模型 縱向四極子是指力向量平行且呈直線排列,如右上角的下方圖形所示。與較簡單的聲源一樣,該四極子被視為四個點單極子的集合,每對單極子在縱向方向上相隔有限距離d ,兩對單極子在縱向方向上相隔距離D 。以下公式是聲壓的表示式,其中Q 為點單極子的源函式。[ 29]
p ( r , θ , t ) = Q Z 0 k 4 π r ( 4 k 2 d D ) cos 2 θ e i ( ω t − k r ) {\displaystyle p(r,\theta ,t)={\frac {QZ{}_{0}k}{4\pi r}}(4{{k}^{2}}dD){{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}}
更直觀的方法是使用導數法。由於偶極子的速度勢是透過單極子的導數獲得的,因此縱向四極子的速度勢可以透過偶極子速度勢的導數獲得。對於縱向四極子,導數是在與主偶極子軸相同的方向上取的。這種方法揭示了作用在體積上的拉伸力。第一個公式是速度勢;第二個是聲壓;第三個是平均平方聲壓。縱向四極聲源可以表示為作用在體積上的拉伸力的變化率的時間平均平方 。
這種四極子的指向性如右側圖所示。三維形式很像一個拉長的氣球。
縱向四極子的指向性 φ ( r , θ , t ) = 3 F 4 π k Z 0 [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos 2 θ e i ( ω t − k r ) p ( r , θ , t ) = i 3 F 4 π [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos 2 θ e i ( ω t − k r ) p 2 ¯ ( r , θ ) = 9 ( ∂ F ∂ t ) 2 ¯ 16 π 2 [ 4 + k 4 r 4 r 6 ] cos 4 θ {\displaystyle {\begin{aligned}&\varphi (r,\theta ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{4}}\theta \\\end{aligned}}}
其中時間導數表示作用在介質上的時變應力。
與橫向四極子類似,必須選擇特徵尺寸L 和特徵速度U 。以下聲功率方程式使用點縱向四極子在離散頻率下的波動應力τ (尺寸為F/L)的簡化表示式。同樣,應力項可以被無量綱版本替換,頻率項被斯特勞哈爾數替換。下面的公式類似於橫向四極子的公式。
W = k 4 τ 2 40 π Z 0 τ ^ = τ ρ 0 U 2 L 3 S = f L U W = 2 π 3 ρ 0 5 c 0 5 S 4 τ ^ 2 U 8 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{4}}{{\tau }^{2}}}{40\pi {{Z}_{0}}}}\\&{\widehat {\tau }}={\frac {\tau }{{{\rho }_{0}}{{U}^{2}}{{L}^{3}}}}\\&S={\frac {fL}{U}}\\&W={\frac {2{{\pi }^{3}}{{\rho }_{0}}}{5c_{0}^{5}}}{{S}^{4}}{{\widehat {\tau }}^{2}}{{U}^{8}}{{L}^{2}}\\\end{aligned}}}
一個縱向四極子類聲場的示範是音叉。[30]
↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952 ↑ http://jullio.pe.kr/fluent6.1/help/html/acoustics/node4.htm ↑ Dawkins, S. "Aguide to Aeroacoustics", Bibliobazaar, 2011 ↑ Norton, M. Karczub, D. "Fundamentals of Noise and Vibration Analysis for Engineers" Cambridge University Press, 2003 ↑ http://gizmodo.com/5977824/the-biggest-bomb-in-the-history-of-the-world ↑ Kinlser, L.E., Frey, A.R., "fundamentals of Acoustics, John wiley and sons, 1962 ↑ Morse, P.M., Ingard, K.U. "Theoretical Acoustics", McGraw-Hill, 1968 ↑ https://sciam.tw/article/aerodynamic-whistles/ ↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952 ↑ Bernhard, R.J., Sandberg, U., "Where Does It Come From?", National Cooperative Highway Research Program, Report 630 ↑ http://ccrllc/files/Tools-for-Analyzing-Sound-Sources.pdf ↑ Powell, A. "Theory of Vortex Sound," Jo. Acoust. Soc. Am., 36, 177-194, 1964 ↑ Powell, A. "Vortex Sound: An alternative derivation of Mohring's formulation" Jo. Acoust. Soc. Am., 97, 684-686, 1995a ↑ Powell, A. "Vortex Sound Theory: Direct proof of equivalence of "vortex force" and "vorticity alone" formulations, n" Jo. Acoust. Soc. Am., 97, 1534-1537, 1995b ↑ Howe, M.S. "Vortex Sound", Cambridge University Press, 2003 ↑ Strouhal, V. "Ueber eine besondere Art der Tonerregung" (On an unusual sort of sound excitation), Annalen der Physik und Chemie, 3rd series, 5 (10) : 216–251, 1878 ↑ Phillips, O.M., "The intensity of Aeolian tones" Jo., Fluid Mech., 1, 607-624, 1956 ↑ Chanaud, R.C., Powell, A., "Some experiments concerning the hole and ring tone", Jo. Acoust. Soc. Am., 37, 5, 902-911, 1965 ↑ Vonnegut, B. "The Vortex Whistle" Jo. Acoust. Soc. Amer. 26, 16-20, 1952 ↑ Chanaud, R.C., "Experiments Concerning the Vortex Whistle", Jo. Acoust. Soc., Amer. 35, No. 7, 953-960, 1963 ↑ Powell, A., "On the Edge Tone", Jo. Acoust. Soc. Amer., 33, No. 4, 395-409, 1961 ↑ Hayden, R.E., Fox, H.L., Chanaud, R.C. "Some Factors Influencing Radiation from flow interaction with edges of finite Surfaces", NASA Cr-145073, 1976 ↑ Russell, D.A., Titlow, J.P., Bemmen,Y, "Acoustic monopoles, dipoles and quadrupoles:an experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Dowling, A.P., ‘‘Steady-State Radiation From Sources,'’ Encyclopedia of Acoustics, . John Wiley and Sons, Chap. 9, 107–125, 1997. ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Powell, A. Class Notes, UCLA, 1961 ↑ Lush, P.A., "Measurements of subsonic jet noise and comparison with theory", Jo. Fluid Mech. 46,3, 477-500, 1971 ↑ Goldstein, M. E., "A generalized acoustic analogy", Jo. Fluid Mech. 488, 315-333, 2003 ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Russell, D.A., "On the sound field radiated by a tuning fork" Am. J. Phys. 68 ~121, December 2000 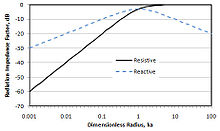
































![{\displaystyle c_{0}^{2}(\rho -{{\rho }_{0}})={\frac {{\partial }^{2}}{\partial {{x}_{i}}{{x}_{j}}}}\int \limits _{V}{\left[{{T}_{ij}}\right]}{\frac {{{d}^{3}}y}{4\pi r}}-{\frac {\partial }{\partial {{x}_{i}}}}\oint \limits _{S}{\left[\rho {{u}_{i}}{{u}_{j}}+p_{ij}^{'}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}+{\frac {\partial }{\partial t}}\oint \limits _{S}{\left[\rho {{u}_{j}}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b75483b43dfda630514a935e11f85e64fa8b441)








![{\displaystyle {\begin{aligned}&p\left(r,t\right)=\left[{\frac {1}{1+ika}}\right]\left({\frac {a}{r}}\right){{Z}_{0}}{{u}_{a}}{{e}^{i\left(\omega t-k\left(r-a\right)\right)}}\\&k={\frac {\omega }{{c}_{0}}}={\frac {2\pi f}{{c}_{0}}}={\frac {2\pi }{\lambda }}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73821e313ba5c6f749792edaad70ba69052dc31b)
![{\displaystyle W=2Au_{a}^{2}R\left[1+{\frac {\sin(2kh)}{2kh}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61c0c7483b62e0510bab6db4a734796cba55657)
![{\displaystyle W=Au_{1}^{2}R\left[1+\left({\frac {u_{2}^{2}}{u_{1}^{2}}}\right)+{\frac {2{{u}_{2}}}{{u}_{1}}}{\frac {\sin(2kh)}{2kh}}\cos \delta \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c271455b9ec11dd922eafd6cb6b590bc26dba8cd)








![{\displaystyle \phi (r,\theta ,t)={\frac {3{{F}_{z}}}{4\pi k{{Z}_{0}}}}\left[{\frac {1+ikr}{{r}^{2}}}\right]\cos \theta {{e}^{i(\omega t-kr)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5433288c4aa534d458a1976b7981e26f515abce)


![{\displaystyle {\begin{aligned}&{{I}_{r}}(r,\theta )={\frac {9F_{z}^{2}}{16{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})}}=+i{\frac {2+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]co{{s}^{2}}\theta \\&{{I}_{\theta }}(r,\theta )={\frac {i9F_{z}^{2}}{32{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {1+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]sin2\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0842d36a36d888a65e0db69beb76a961c8af59b7)
![{\displaystyle W={\frac {3F_{z}^{2}}{4\pi {{a}^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{a}^{2}}}{1+{{k}^{2}}{{a}^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d8a806d04578d204f18dca05da85cfdcead473)

![{\displaystyle p{{p}^{*}}={\frac {9F_{z}^{2}}{16{{\pi }^{2}}(1+{{k}^{2}}{{a}^{2}})}}\left[{\frac {(1+{{k}^{2}}r_{1}^{2})}{r_{1}^{4}}}{{\cos }^{2}}{{\alpha }_{1}}+{\frac {(1+{{k}^{2}}r_{2}^{2})}{r_{2}^{4}}}{{\cos }^{2}}{{\alpha }_{2}}+{\frac {2\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}}{r_{1}^{2}r_{2}^{2}}}\left[(1+k{{r}_{1}}{{r}_{2}})\cos k({{r}_{2}}-{{r}_{1}})+k({{r}_{2}}-{{r}_{1}})\sin k({{r}_{2}}-{{r}_{1}})\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddacaf278928a5fe82cfdbe6dd75d4be89e84f21)




![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,\psi ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,\psi ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta ,\psi )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{2}}\theta {{\sin }^{2}}{{\cos }^{2}}\psi \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb6ceed5f4392505cfd9188503024dd4c31890ef)



![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{4}}\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d444c5c2ff5c9d89cf361f3e3a3bcce3f2d97d60)
