代數/第 4 章/複合不等式和絕對值不等式

代數

代數/第 4 章
← 方程組	複合不等式和絕對值不等式	其他型別的圖形 →

複合不等式是兩個不等式作為同一個問題呈現。根據使用“和”或“或”的詞語，被求解的變數可能只需要滿足其中一個不等式或兩者都需要滿足。可能存在許多正確的答案，甚至可能完全沒有答案。

示例：2x - 4 > 2 或 30/x > 15

然後可以將答案繪製為數軸上的兩條射線。

如果我們對實數解感興趣，我們可以選擇幾乎小於 2 或幾乎大於 3 的數字，因為我們想要什麼，方程都將成立。例如，如果 x =1.99，則 30/x = 15.08（滿足 30/x > 15）或如果 x = 3.01，則 2x-4 = 2.02（滿足 2x -4 > 2）。

如果我們只對整數解感興趣，那麼我們可以看到，除了 2 或 3 之外的所有整數都將起作用。

我們還可以將複合不等式表示為函式。

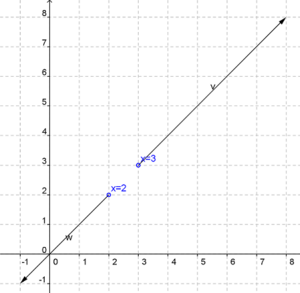
如果我們指定一個函式 f(x) = (x > 3 或 x < 2)，我們得到一個這樣的圖形

解仍然是兩條射線。但是現在射線位於直線 y=x 上，一條射線從數字 3 向右向上移動，另一條射線從數字 2 向左向下移動。

練習：使用斜率的概念，你能解釋為什麼從數軸轉移到笛卡爾圖形的圖形總是顯示在直線 y=x 上嗎？

如何使用複合不等式？

汽車上的燃油里程標籤會給出兩個數字：一個是城市駕駛，另一個是高速公路駕駛。如果標籤說汽車在城市中能行駛 25 英里/加侖，在高速公路上能行駛 32 英里/加侖，那麼你能行駛多遠？

為了找出答案，我需要知道油箱裡有多少油。我知道我可以用一加侖油行駛 25 到 32 英里。我可以使用兩個方程來表示這一點，其中 x = 我可以用一加侖油行駛的距離

25 < x 且 x < 32。

或者我可以將它們組合成一個複合不等式

25 < x < 32。

如果我的油箱是 10 加侖，並且我想知道我能行駛多遠，我會將方程改為表示我的油箱中 10 加侖油，方法是將複合不等式中的每一項乘以 10。

25 * 10 < 10*x < 32 * 10。

250 < 10x < 320。

我可以用一箱油行駛 250 到 320 英里。

華氏度到攝氏度的轉換公式為 5/9(F - 32)。

我們知道水在 32 華氏度結冰，在 212 華氏度沸騰。

如果我們想知道水的冰點和沸點用攝氏度表示，我們可以將方程設定如下

32 < F < 212

然後應用公式將華氏度的值轉換為攝氏度。

5/9(32-32) < C < 5/9(212 - 32)

所以水的冰點和沸點為

0 < C < 100

當我們需要乘以 x 時會發生什麼？

請記住，減法等同於加一個負數，乘法等同於加一個數多次。因此，當我們多次加一個負數時，結果會越來越小。在使用不等式求解問題時，我們需要確定問題的背景對於負數是否合理。

一種特殊的複合不等式涉及絕對值符號。絕對值符號指定兩個函式，使得 f(x)=A 意味著 f(-x) = (-A)(-1)。對於等號，這與 f(x)=f(-x)=A 相同。但是，當我們使用不等號並乘以負數時，我們必須改變符號的方向。因此，如果 f(x) > A，那麼 f(-x) < A。

當只有 x 的值在絕對值符號中時，這很簡單。例如，給出 |x| > 12，那麼可能的解是 x > 12 或 x < -12。

三個絕對值問題的例子。
右邊為正數	右邊為零	右邊為負數
$\|x\|-12>0$	$\|x\|+12>12$	$\|x\|+12>0$
$\|x\|>12$	$\|x\|>0$	$\|x\|>-12$
$x>12{\text{ or }}x<-12$	$x>0{\text{ or }}x<0$	${\text{all numbers }}x{\text{ satisfy }}\|x\|>-12$
12 和 -12 之間的間隙。	除了 0 之外的任何數字。	任何數字。