核醫學基礎物理/伽馬射線衰減

康普頓效應

我們在上一章從描述的角度介紹了伽馬射線與物質的相互作用，並發現康普頓效應和光電效應是主要的機制。我們將在本章再次考慮這個主題，但這次是從分析的角度。這將使我們能夠對這種現象有更一般的理解。

注意，這裡討論的治療也適用於X射線的衰減，因為正如我們之前提到的，伽馬射線和X射線本質上是相同的物理實體。

我們的討論從一個簡單的輻射實驗的描述開始，這個實驗可以在實驗室中輕鬆完成，許多早期領域的先驅者都做過這個實驗。然後，我們將利用從這些實驗中獲得的資訊來開發一個簡單的方程和一些簡單的概念，這些概念將使我們能夠將情況推廣到任何衰減情況。

衰減實驗

實驗很簡單。它涉及到將一束狹窄的伽馬射線射向一種材料，並測量有多少輻射穿透。我們可以改變我們使用的伽馬射線的能量，以及吸收材料的型別及其厚度和密度。

下圖顯示了實驗裝置。我們將入射到吸收體的輻射強度稱為入射強度，I₀，穿過吸收體的輻射強度稱為透射強度，I_x。請注意，吸收體的厚度用x表示。

從我們在上一章中介紹的內容可以看出，一些伽馬射線在穿過吸收體時會發生光電效應和康普頓效應等相互作用。透射的伽馬射線主要是那些完全沒有發生相互作用的伽馬射線。

因此，我們可以預期透射強度將小於入射強度，即

$I_{x}<I_{0}\,\!$

但你可能會問，到底小多少呢？在我們考慮這一點之前，讓我們將I_x和I₀之間的差值記為∆I，即

$\Delta I=I_{0}-I_{x}\,\!$

原子序數的影響

讓我們從將不同的吸收體依次放置在輻射束中來開始探索∆I的大小。我們會發現∆I的大小高度依賴於吸收材料的原子序數。例如，我們會發現對於由碳（Z=6）製成的吸收體，∆I會相當低，而對於由鉛（Z=82）製成的吸收體，∆I會非常大。

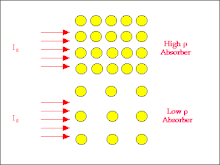
我們可以從下圖瞭解為什麼會出現這種情況

該圖用大的圓圈代表原子，表示高原子序數的吸收體，用小的圓圈代表原子，表示低原子序數的材料。入射輻射束由從左側進入每個吸收體的箭頭表示。請注意，高原子序數吸收體的原子為輻射提供了更大的靶區，因此透過光電效應和康普頓效應發生相互作用的可能性相對較高。因此衰減應該相對較大。

然而，在低原子序數吸收體的情況下，單個原子更小，因此發生相互作用的可能性降低。換句話說，輻射更有可能穿過吸收體，因此衰減比高原子序數情況下的衰減低。

在我們在上一章中使用的宇宙飛船類比中，原子序數可以被認為是流星雲中單個流星的大小。

如果我們能夠精確控制實驗裝置並仔細分析我們的結果，我們會發現

$\Delta I\propto Z^{3}\,\!$

因此，如果我們將吸收體的原子序數增加一倍，我們就會將衰減增加到兩倍的三次方，即8倍；如果我們將原子序數增加到三倍，我們就會將衰減增加到三倍的三次方，即27倍，等等。

正是由於這個原因，高原子序數材料（例如Pb）被用於輻射防護。

密度的影響

探索∆I大小的第二種方法是觀察當我們改變吸收體密度時會發生什麼。我們可以從下圖看到，低密度吸收體產生的衰減比高密度吸收體產生的衰減小，因為輻射與吸收體原子之間發生相互作用的可能性相對較低。此外，密度決定了與樣品相關的透射係數，因為密度越低，透射係數越高，因為材料的孔隙率更高。

因此，在宇宙飛船進入流星雲的類比中，想象一下不同密度的流星雲以及宇宙飛船與流星發生碰撞的可能性。

厚度的影響

我們可以改變的第三個因素是吸收體的厚度。正如你應該能夠在這個階段預測的那樣，吸收體越厚，衰減越大。

伽馬射線能量的影響

在我們的實驗中，我們能夠改變伽馬射線束的能量。我們發現，雖然不深入探討細節，但伽馬射線的能量越高，衰減越小。你可以把它想象成宇宙飛船以不同的能量接近流星雲，能量低的宇宙飛船穿過的可能性較小，而能量高的宇宙飛船穿過的可能性較大。

數學模型

這裡我們將考慮一個數學模型，它將幫助我們用更一般的術語表達我們的實驗觀察結果。你會發現，採用的數學方法和得到的結果與我們之前在放射性衰變定律中遇到的非常相似。所以你不需要再費力地學習新的數學知識，只需要對相同形式的數學分析進行不同的應用！

讓我們從最簡單的情況開始，假設我們只改變吸收體的厚度。換句話說，我們使用相同材料（即相同原子序數）和相同密度的吸收體，並使用相同能量的伽馬射線進行實驗。只有吸收體的厚度發生了改變。

從我們上面的推理中不難理解，∆I 的大小應該取決於輻射強度以及吸收體的厚度，也就是說，對於吸收體厚度微小的變化

$-dI\propto I\cdot dx\,\!$

負號表示強度因吸收體而減小。

將這個等式中的比例關係轉化為等式，我們可以寫成

$-dI=\mu I\cdot dx\,\!$

其中比例常數 μ 稱為線性衰減係數。

除以 I，我們可以將這個等式改寫為

$-{\frac {dI}{I}}=\mu \cdot dx$

所以這個等式描述了對於任何微小的吸收體厚度變化 dx 的情況。要找出對於吸收體的完整厚度會發生什麼，我們只需將每個小厚度上發生的情況加起來即可。換句話說，我們將上述等式積分。更正式地表達，我們可以說，對於從 x = 0 到任何其他厚度 x 的厚度，輻射強度將從 I₀ 減少到 I_x，因此

$-\int _{I_{0}}^{I_{x}}{\frac {dI}{I}}=\mu \int _{0}^{x}dx$

$\therefore \ln \left({\frac {I_{x}}{I_{0}}}\right)=-\mu x$

$\therefore {\frac {I_{x}}{I_{0}}}={\text{exp}}\ (-\mu x)$

$\therefore I_{x}=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

這個最終的表示式告訴我們，輻射強度將隨著吸收體的厚度以指數方式減小，減小的速率由線性衰減係數控制。該表示式在下面的圖形中顯示。該圖繪製了強度與厚度 x 的關係。我們可以看到，強度從 I₀ 開始減小，即 x = 0 處的數值，最初以較快的速度減小，然後以經典的指數方式減慢。

輻射強度對吸收體厚度的依賴關係的圖形表示：左側為強度與厚度的關係，右側為強度自然對數與厚度的關係。

線性衰減係數的影響可以在下一張圖中看到。這裡的所有三條曲線都是指數性質的，只有線性衰減係數不同。注意，當線性衰減係數較小時，曲線下降得比較慢，當線性衰減係數較大時，曲線下降得很快。

使用小、中、大線性衰減係數 µ 表示的指數衰減。

線性衰減係數是單個吸收材料的特徵。有些材料，比如碳，其值較小，很容易被伽馬射線穿透。其他材料，比如鉛，其線性衰減係數相對較大，是相對較好的輻射吸收體。

各種材料在 100、200 和 500 keV 伽馬射線能量下的線性衰減係數 (cm^-1)。

吸收體	100 keV	200 keV	500 keV
空氣	0.000195	0.000159	0.000112
水	0.167	0.136	0.097
碳	0.335	0.274	0.196
鋁	0.435	0.324	0.227
鐵	2.72	1.09	0.655
銅	3.8	1.309	0.73
鉛	59.7	10.15	1.64

上表中列出的材料為空氣、水以及從碳 (Z=6) 到鉛 (Z=82) 的一系列元素，並給出了三種伽馬射線能量下的線性衰減係數。第一個需要注意的是，線性衰減係數隨著吸收體原子序數的增加而增加。例如，它從空氣在 100 keV 下的 0.000195 cm^-1 的很小的值增加到鉛的近 60 cm^-1。第二個需要注意的是，所有材料的線性衰減係數都隨著伽馬射線能量的增加而減小。例如，銅的值從 100 keV 下的約 3.8 cm^-1 減少到 500 keV 下的 0.73 cm^-1。第三個需要注意的是，表中的趨勢與前面介紹的分析一致。

最後，重要的是要認識到，我們上面的分析只在處理狹窄的輻射束時才嚴格成立。當涉及到寬輻射束時，需要考慮其他因素。

半值層

與使用半衰期描述放射性衰變定律一樣，通常從上面的指數衰減方程中推匯出一個指標，它有助於我們更清楚地理解正在發生的事情。這個指標稱為半值層，它表示將入射輻射強度降低一半所需的吸收材料厚度。從圖形的角度來看，我們可以說，當

$I_{x}={\frac {I_{0}}{2}}$

吸收體的厚度是半值層

下表列出了三種伽馬射線能量下各種吸收體的半值層

三種伽馬射線能量下各種材料的半值層（單位：釐米）。

吸收體	100 keV	200 keV	500 keV
空氣	3555	4359	6189
水	4.15	5.1	7.15
碳	2.07	2.53	3.54
鋁	1.59	2.14	3.05
鐵	0.26	0.64	1.06
銅	0.18	0.53	0.95
鉛	0.012	0.068	0.42

首先要注意的是，半值層隨著原子序數的增加而減小。例如，空氣在 100 keV 的半值層約為 35 米，而鉛在該能量下的半值層僅為 0.12 毫米。換句話說，需要 35 米的空氣才能將 100 keV 伽馬射線束的強度降低一半，而 0.12 毫米的鉛就能做到同樣的事情。第二點要注意的是，半值層隨著伽馬射線能量的增加而增加。例如，銅在 100 keV 的半值層為 0.18 釐米，而在 500 keV 的半值層約為 1 釐米。第三點要注意的是，相對於上一張表格中的資料，半值層和線性衰減係數之間存在倒數關係，我們現在將對其進行研究。

μ 和半值層之間的關係

正如我們在放射性衰變定律中探索了半衰期和衰變常數之間的關係一樣，我們也可以推匯出半值層和線性衰減係數之間的關係。我們可以透過使用半值層的定義來實現這一點

$I={\frac {I_{0}}{2}}$

當

$x=x_{\frac {1}{2}}$

並將它代入指數衰減方程，即

$I=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

得到

${\frac {I_{0}}{2}}=I_{0}\ {\text{exp}}\ (-\mu x_{\frac {1}{2}})$

因此

${\frac {1}{2}}={\text{exp}}\ (-\mu x_{\frac {1}{2}})$

$\therefore 2^{-1}={\text{exp}}\ (-\mu x_{\frac {1}{2}})$

$\therefore \ln 2^{-1}=-\mu x_{\frac {1}{2}}$

$\therefore \ln 2=\mu x_{\frac {1}{2}}$

$\therefore 0.693=\mu x_{\frac {1}{2}}$

$\mu ={\frac {0.693}{x_{\frac {1}{2}}}}$

和

$x_{\frac {1}{2}}={\frac {0.693}{\mu }}$

這兩個公式表達了線性衰減係數和半值層之間的關係。在解決與衰減相關的數值問題時，它們非常有用，並且通常是解決數值問題的第一步。

質量衰減係數

我們在上面暗示了線性衰減係數在考慮相同密度但不同厚度的吸收材料時非常有用。當我們希望將吸收體的密度 ρ 納入分析時，一個相關的係數可能會有價值。這就是質量衰減係數，定義為

${\frac {\text{Linear Attenuation Coefficient}}{\text{Density}}}={\frac {\mu }{\rho }}$

上面表格中使用的線性衰減係數的測量單位是 cm^-1，密度的常用單位是 g cm^-3。您可能想根據此基礎自行推匯出 cm² g^-1 是質量衰減係數的等效單位。

問題

下面給出兩個問題，以幫助您加深對本章內容的理解。第一個問題比較直接，將鍛鍊您對指數衰減公式的應用。第二個問題更具挑戰性，將幫助您將指數衰減與放射性和輻射照射聯絡起來。

問題 1

需要多少鋁才能將 200 keV 伽馬射線束的強度降低到其入射強度的 10%？假設 200 keV 伽馬射線在 Al 中的半值層為 2.14 cm。

答案

用上述符號表示的問題是

$I={\frac {I_{0}}{10}},\ {\text{when}}\ x={\text{?}}$

我們知道半值層為 2.14 cm。因此，線性衰減係數為

$\mu ={\frac {0.693}{x_{\frac {1}{2}}}}={\frac {0.693}{2.14}}=0.324\ {\text{cm}}^{-1}$

現在將所有這些與指數衰減公式結合起來

$I=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

我們可以寫

${\frac {I_{0}}{10}}=I_{0}\ {\text{exp}}\ (-0.324x)$

因此

${\frac {1}{10}}={\text{exp}}\ (-0.324x)$

$\therefore -\ln 10=-0.324x$

$\therefore x={\frac {\ln 10}{0.324}}={\frac {2.3}{0.324}}=7.1\ {\text{cm}}$

$\therefore x\approx 7\ {\text{cm}}$

因此，將這些伽馬射線降低十倍所需的鋁厚度約為 7 釐米。這種相對較大的厚度是鋁通常不用於輻射防護的原因 - 它的原子序數不足以有效地顯著衰減伽馬射線。

您可以嘗試將 Pb 作為吸收體的情況 - 但您需要自己找出 200 keV 伽馬射線在 Pb 中的半值層！

這裡有一個提示：檢視上面的表格之一。

以下為您提供答案，供您檢查完成後核對：2.2 毫米。

換句話說，需要相對較薄的 Pb 厚度才能達到與 7 釐米鋁相同的效果。

問題 2

一個 10⁵ MBq 的¹³⁷Cs 源需要裝在 Pb 盒子裡，以便源頭 1 米處的照射率小於 0.5 mR/小時。如果¹³⁷Cs 伽馬射線在 Pb 中的半值層為 0.6 釐米，則需要多厚的 Pb？¹³⁷Cs 的比伽馬射線常數在 1 釐米處為 3.3 R hr^-1 mCi^-1。

答案

這是一個相當典型的例子，它出現在人們使用放射性物質時。我們希望使用一定量的物質，並將它儲存在鉛容器中，以便在安全距離內工作的照射率低於某個安全水平。我們知道將要使用的物質的放射性。但它用 SI 單位表示。我們查閱參考書，發現該放射性同位素的照射率以傳統單位表示。就像我們的問題一樣！

因此，讓我們首先將單位統一。比伽馬射線常數給出為

3.3 R hr^-1 mCi^-1 在距離源頭 1 釐米處。

這等於

3300 mR hr^-1 mCi^-1 在距離源頭 1 釐米處，

這等於

${\frac {3300}{(100)^{2}}}\ {\text{mR hr}}^{-1}\ {\text{mCi}}^{-1}\ {\text{at 1 m from the source}}$

基於平方反比定律。該結果按貝克勒爾表示為

${\frac {3300}{10^{4}(3.7\cdot 10^{7})}}\ {\text{mR hr}}^{-1}\ {\text{Bq}}^{-1}\ {\text{at 1 m from the source}}$

因為 1 mCi = 3.7 x 10⁷ Bq。因此，對於 10⁵ MBq，曝光率為

${\frac {3300\cdot 10^{5}\cdot 10^{6}}{10^{4}(3.7\cdot 10^{7})}}\ {\text{mR hr}}^{-1}\ (10^{5}\ {\text{MBq}})^{-1}\ {\text{at 1 m from the source}}$

也就是說，我們源頭1米處的曝光率為891.9 mR hr^-1。

我們希望根據問題將該曝光率降低到 0.5 mR hr^-1以下，使用鉛來實現。

在此階段，您應該能夠使用指數衰減方程和這些伽馬射線在鉛中的半值層來計算所需的鉛厚度約為6.5 釐米。

外部連結

• Mucal on the Web - 由伊利諾伊理工學院同步輻射研究與儀器中心 Pathikrit Bandyopadhyay 提供的線上程式，用於計算 X 射線吸收係數。
• Tables of X-Ray Mass Attenuation Coefficients - 來自美國國家標準與技術研究院的大量資料，涵蓋所有元素。