生物醫學工程理論與實踐/生理建模與模擬

計算資源效率的提高和成本的降低對建模和設計產生了巨大的影響。強大的計算機工作站和軟體或程式語言（例如，MATLAB、LabView、wxMaxima、R 等等）的易用性允許互動式設計高效能、魯棒的控制器。故障風險往往阻礙了在活人身上設計和評估控制器的可能性，因此，裝置和治療方法通常首先在計算機和動物模型上進行測試。過去，動物一直是首選，但這種方法不斷受到重新評估，因為動物很少是人類疾病和狀況的完美模型。組織培養開始滿足這種需求的一部分，計算機建模和模擬也可以做到這一點。如今，計算機模型被用於 (1) 證明可行性，(2) 透過補充動物研究來提高對控制器設計的信心，(3) 幫助設計更好的動物和臨床實驗，以及 (4) 減少所需的動物和人體實驗數量。未來，計算機模型的應用將進一步擴充套件。

生理系統基本模型-隔室模型

這種分析涉及將生理系統劃分為若干相互連線的隔室 - 其中隔室可以是系統的任何解剖學、生理學、化學或物理亞部分。一個基本假設是示蹤劑在整個隔室中均勻分佈。在各種隔室模型中，最簡單的模型是單隔室模型。

單隔室模型

圖 4.1. 單隔室模型

圖 4.2. 示蹤劑數量 q 相對於時間變化的圖形說明，對應於相對高和低的週轉率 k 值。

圖 4.1 顯示了一個單隔室模型，其中示蹤劑透過血管的流動遵循理想的脈衝注射。該系統中的隔室是封閉的，除了示蹤劑的流入和流出，示蹤劑被注射，如圖所示。在這個理論中，示蹤劑將根據其注射立即並均勻地在整個隔室中混合。其數量將隨著時間的推移而減少，這取決於流出率。該系統中使用的變數是

q：時間 t 時隔室中示蹤劑的數量，以及
F：流出量。

如果我們將週轉率 k 定義為這兩個引數的比率，即

$k={\frac {-dq/dt}{q}}$

它可以改寫為

${\frac {dq}{dt}}=-kq$

該方程的解是

$q=q_{0}\ exp(-kt)\,\!$

其中 q_o 是時間 t = 0 時存在的示蹤劑數量。該方程在圖 4.2 中繪製。

雙隔室模型-封閉系統

圖 4.3 封閉雙隔室模型

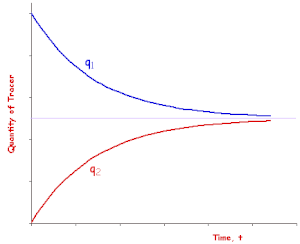圖 4.4 封閉隔室模型中隔室 #1 和 #2 中示蹤劑數量隨時間的變化。

在封閉系統中，示蹤劑只是在兩個隔室之間移動，沒有整體的損失或增益，如圖 4.3 所示。因此，

${\frac {dq_{1}}{dt}}=k_{21}q_{2}-k_{12}q_{1}$ 和 ${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$.

由於系統中沒有示蹤劑損失，

$q_{1}+q_{2}={\text{constant}}=q_{0}\,\!$

因此，

${\frac {dq_{1}}{dt}}=-{\frac {dq_{2}}{dt}}\,,$

隨著隔室 #1 中示蹤劑數量的減少，隔室 #2 中的數量會增加，反之亦然。當示蹤劑在時間 t = 0 時被注射到隔室 #1 中時，

$q_{1}=q_{0}\,\!$

和

$q_{2}=0\,,\,\!$

因此，在初始階段

${\frac {dq_{1}}{dt}}=-k_{12}q_{0}$

和

${\frac {dq_{2}}{dt}}=k_{12}q_{0}$

該系統的解為

$q_{1}=q_{0}\left\lbrack 1-{\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

和

$q_{2}=q_{0}\left\lbrack {\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

圖 4.4 顯示瞭如果隔室體積相同，則這些系統之一。

雙隔室模型 - 開放鏈狀系統

兩個隔室像鏈一樣連線，最後一個隔室有一個匯，如圖 4.5 所示。

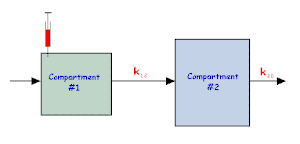圖 4.5 開放鏈狀雙隔室模型。

圖 4.6 開放鏈狀雙隔室模型中示蹤劑數量隨時間的變化。

在這個模型中，

${\frac {dq_{1}}{dt}}=-k_{12}q_{1}$ 和 ${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{20}q_{2}$

這些方程的解為

$q_{1}=q_{0}\ {\text{exp}}(-k_{12}t)$

和

$q_{2}=q_{0}{\frac {k_{12}}{k_{12}-k_{20}}}\lbrack {\text{exp}}(-k_{20}t)-{\text{exp}}(-k_{12}t)\rbrack \,,$

並且 q₁ 和 q₂ 的行為如圖 4.6 所示。

雙隔室模型 - 開放乳頭狀系統

中央隔室有一個匯，它與其他隔室無關。雖然這些隔室不一定具有生理意義，但常見的名稱是

• 隔室 1（中央） - 血液和良好灌注的器官，例如肝臟、腎臟等；“血漿”
• 隔室 2（外圍） - 灌注不良的組織，例如肌肉、瘦肉組織、脂肪；“組織”

圖 4.7 開放乳頭狀雙隔室模型。

圖 4.8 開放乳頭狀雙隔室模型中示蹤劑數量隨時間的變化。

在這種情況下，

${\frac {dq_{1}}{dt}}=-k_{10}q_{1}-k_{12}q_{1}+k_{21}q_{2}$ 和 ${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$

當 *t* = 0 時

$q_{1}=q_{0}\,\!$ 和 $q_{2}=0\,\!$

所以，解為

$q_{1}=q_{0}\left\lbrack {\frac {k_{21}-a_{1}}{a_{2}-a_{1}}}{\text{exp}}(-a_{1}t)+{\frac {k_{21}-a_{2}}{a_{1}-a_{2}}}{\text{exp}}(-a_{2}t)\right\rbrack$ 和

$q_{2}={\frac {q_{0}k_{12}}{a_{2}-a_{1}}}\lbrack {\text{exp}}(-a_{1}t)-{\text{exp}}(-a_{2}t)\rbrack$

心血管模型和控制

心血管系統建模

呼吸模型和控制

另請參閱 人類呼吸控制系統數學模型

呼吸系統建模

用於生理控制的神經網路

另請參閱 用於控制人類運動的分散式神經網路：來自正常人和脊髓損傷患者的經驗教訓。

術語“神經網路”通常指的是一類計算演算法，這些演算法鬆散地基於神經系統的計算結構。換句話說，神經網路的設計包括指定神經元、架構和學習演算法。

運動的外部控制

另請參閱 運動的外部控制

快速眼動控制系統

另請參閱 維基百科，眼動

進一步閱讀

• Bronzino, Joseph D. (2006 年 4 月). 生物醫學工程手冊，第三版. [CRC 出版社]. ISBN 978-0-8493-2124-5.
• Villafane, Carlos, CBET. (2009 年 6 月). 生物醫學：從學生的角度，第一版. [Techniciansfriend.com]. ISBN 978-1-61539-663-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
• 與生物醫學工程相關的資料。

參考資料

1. 生物學與醫學中的區室分析，第 2 版，密歇根大學出版社，1985 年。
2. Evans, W. C.，線性系統、隔室模型和 IAQ 研究中的可估計性問題，見 Tichenor, B.，室內空氣汙染源及其相關匯效應特徵，ASTM STP 1287，第 239-262 頁，1996 年 ISBN 0-8031-2030-3。
3. Bronzino J. (編) 生物醫學工程手冊，3 卷套。 (第 3 版，CRC，2006)ISBN 0849321212