變分法/第六章

第六章：微分方程 $G=0$ 的解的形式。

• 87 微分方程 $G=0$ 的另一種形式。
• 88 函式 $F_{1}$ 的另一種形式。
• 89 冪級數積分。
• 90 微分方程 $G=0$ 的解 $x=\phi (t,\alpha ,\beta )$，$y=\psi (t,\alpha ,\beta )$。
• 91，92 當 $F_{1}=0$ 在曲線的初始點時。
• 93 當 $s$ 是自變數時，微分方程 $G=0$ 的形式。
• 94 該方程的解。
• 95 曲線在所討論的區間內不能有奇點。曲線中任意點的座標用 $s$ 的冪級數表示。

第 87 條.
在我們繼續研究積分

$I=\int _{t_{0}}^{t_{1}}F(x,y,x',y')~{\text{d}}t{\text{,}}\qquad {\text{[1]}}$

的最大值或最小值存在的進一步條件之前，我們將努力更仔細地研究微分方程 $G=0$ 的性質和形式。

我們假設滿足微分方程

$G={\frac {\partial ^{2}F}{\partial x\partial y'}}-{\frac {\partial ^{2}F}{\partial y\partial x'}}+F_{1}\left(x'{\frac {{\text{d}}y'}{{\text{d}}t}}-y'{\frac {{\text{d}}x'}{{\text{d}}t}}\right)=0{\text{,}}\qquad {\text{[2]}}$

已知曲線 $F_{1}$ 不等於零，設 $A$ 為曲線的起點，$AA'$ 為曲線在 $A$ 處的方向。假設微分方程 $G=0$ 具有最簡單的形式，如果我們把其中一個座標視為另一個座標的單值函式。在上述積分 $I$ 中，量 $x$，$y$ 對量 $t$ 的依賴性僅受一個條件的限制，即當 $t$ 從 $t_{0}$ 連續遞增到 $t_{1}$ 時，點從起點移動到終點。

我們可以用無限多種方式在 $t$ 的位置引入另一個變數 $\tau$，其中

$t=f(\tau )$

只需要函式 $f$ 的形式滿足以下條件：隨著 $\tau$ 的增加，$\tau$ 也隨之增加。我們可以反過來用

$\tau =\phi (t)$.

再次引入 $\tau$。積分 $I$ 和微分方程 $G=0$ 的形式在這些變換下不會改變。

在某些情況下，我們可以選擇將 $t$ 座標 $x$ 本身作為自變數，這種情況發生在沿著曲線從起點到終點移動時，x 連續增加。特別地，我們可以將 $X$-軸作為起點 $A$ 的切線，並將曲線的走向作為 $X$-軸的正方向。由於我們只考慮正則曲線或由正則部分組成的曲線，因此如果點 $P$ 從點 $A$ 開始沿著曲線移動，它到 $A$ 處的法線的距離在曲線的某個部分連續增加。因此，對於這部分曲線，如果我們將 ${\displaystyle }$ 處的法線的正方向作為正 $Y$-軸，則對於每個 $x$ 值，只有一個 $y$ 值。因此，對於曲線的特定部分，我們可以始終假設，透過適當選擇座標系，第二個座標可以看作是第一個座標的單值函式。因此，我們只需要進行座標變換。

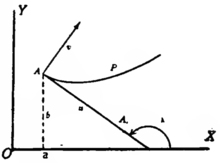
令新座標原點的座標為 $a$，$b$，並且令

$x=a+gu+g'v$，$y=b+hu+h'v$，$\qquad {\text{[3]}}$

其中 $u$ 和 $v$ 是新的座標。

如果 $\lambda$ 是 $X$ 軸和 $u$ 軸之間的夾角，那麼我們有眾所周知的公式

$g=\cos(\lambda )$，$h=\sin(\lambda )$，$g'=-\sin(\lambda )$，$h'=\cos(\lambda )$。 $\qquad {\text{[4]}}$

積分 $I$ 然後變為，因為 $u$ 可以被看作是獨立變數，

$I=\int _{0}^{u}F\left(a+gu+g'v,b+hu+h'v,g+g'{\frac {{\text{d}}v}{{\text{d}}u'}},h+h'{\frac {{\text{d}}v}{{\text{d}}u}}\right)~{\text{d}}u$,

為了簡潔，我們將其表示為

$I=\int _{0}^{u}f\left(u,v,{\frac {{\text{d}}v}{{\text{d}}u}}\right)~{\text{d}}u$。 $\qquad {\text{[5]}}$

如果我們進一步寫出 ${\frac {{\text{d}}v}{{\text{d}}u}}=v'$ 那麼 [5] 變為

$I=\int _{0}^{u}f(u,v,v')~{\text{d}}u$。 $\qquad {\text{[}}5^{\text{a}}{\text{]}}$

如果我們將上一章第 74-80 節中使用的方法應用於此積分，我們將得到一個微分方程來確定 $v$ 作為 $u$ 的函式。

設曲線僅沿縱座標方向滑動 $v$，因此將 $v+{\bar {v}}$ 代替 $v$，其中 ${\bar {v}}$ 是一個非常小的量，在所考慮曲線段的端點和起點處消失。進行變分的積分是

$I+\Delta I=\int f\left(u,v+{\bar {v}},v'+{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}\right)~{\text{d}}u$.

接下來，我們根據 ${\bar {v}}$ 和 ${\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}$ 的冪展開 $\Delta I$。一階項的總和為

$\delta I=\int _{0}^{u}\left({\frac {\partial f}{\partial v}}{\bar {v}}+{\frac {\partial f}{\partial v'}}{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}\right)~{\text{d}}u{\text{,}}\qquad {\text{[6]}}$

或者，因為

${\frac {\partial f}{\partial v'}}{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}={\frac {\text{d}}{{\text{d}}u}}\left({\bar {v}}{\frac {\partial f}{\partial v'}}\right)-{\bar {v}}{\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}$,

我們有

$\delta I=\int _{0}^{u}\left({\frac {\partial f}{\partial v}}-{\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}\right){\bar {v}}~{\text{d}}u+\left[{\bar {v}}{\frac {{\text{d}}f}{{\text{d}}v'}}\right]_{0}^{u}$. $\qquad {\text{[6}}^{a}{\text{]}}$

方括號內的量為零，因為 ${\bar {v}}=0$ 在極限情況下。此外，我們必須有

$\delta I=0$.

由於 ${\bar {v}}$ 是任意的，僅受必須在極限處消失的條件約束，從上一章的引理可知

${\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}-{\frac {\partial f}{\partial v}}=0$,

或者

${\frac {\partial ^{2}f}{\partial ^{2}v'^{2}}}{\frac {{\text{d}}v'}{{\text{d}}u}}+{\frac {\partial ^{2}f}{\partial v\partial v'}}v'+{\frac {\partial ^{2}f}{\partial u\partial v'}}-{\frac {\partial f}{\partial v}}=0$. $\qquad {\text{[2}}^{a}{\text{]}}$

第 88 條.
如果一個座標可以被認為是另一個座標的單值函式，則方程 [$2^{\text{a}}$] 可以代替形式 [2] 用於 $G=0$.

現在我們將證明在 [$2^{\text{a}}$] 中出現的量 ${\frac {\partial ^{2}f}{\partial v'^{2}}}$ 與 $F_{1}$ 相同，前提是在函式 $F(x,y,x',y')$ 中 $x$ 和 $y$ 可以被視為僅是 $u$ 的函式。

因為

$f(u,v,v')\equiv F(a+gu+g'v,b+hu+h'v,g+g'v',h+h'v')\equiv F(x,y,x',y')$,

因此，我們得到

${\frac {\partial f}{\partial v'}}={\frac {\partial F}{\partial x'}}g'+{\frac {\partial F}{\partial y'}}h'$,

因此

${\frac {\partial ^{2}f}{\partial v'^{2}}}={\frac {\partial ^{2}F}{\partial x'^{2}}}g'^{2}+2{\frac {\partial ^{2}F}{\partial x'\partial y'}}g'h'+{\frac {\partial ^{2}F}{\partial y'^{2}}}h'^{2}$.

另一方面，根據其定義，$F_{1}$ 由以下任一關係確定： 

${\frac {\partial ^{2}F}{\partial x'^{2}}}=F_{1}y'^{2}$; ${\frac {\partial ^{2}F}{\partial x'}}{\partial y'}=-F_{1}x'y'$; ${\frac {\partial ^{2}F}{\partial y'^{2}}}=F_{1}x'^{2}$. $\qquad {\text{[7]}}$

由此可知

${\frac {\partial ^{2}f}{\partial v'^{2}}}=(g'^{2}y'^{2}-2g'h'x'y'+h'^{2}x'^{2})F_{1}=(g'y'-h'x')^{2}F_{1}=(g'h-h'g)^{2}F_{1}=(-\sin ^{2}(\lambda )-\cos ^{2}(\lambda ))^{2}F_{1}$;

或者最終，

${\frac {\partial ^{2}f}{\partial v'^{2}}}=F_{1}$. $\qquad {\text{[8]}}$

因此，[$2^{\text{a}}$] 可以寫成

$F_{1}{\frac {{\text{d}}v'}{{\text{d}}u}}+{\frac {\partial ^{2}f}{\partial v\partial v'}}v'+{\frac {\partial ^{2}f}{\partial u\partial v'}}-{\frac {\partial f}{\partial v}}=0$.

因為我們有

$v'={\frac {{\text{d}}v}{{\text{d}}u}}$,

以及

$f(u,v,v')\equiv F(x,y,x',y')$,

其中 $x$，$y$ 由 $u$，$v$ 根據 [3] 確定，可以得出

$F_{1}{\frac {{\text{d}}^{2}v}{{\text{d}}u^{2}}}+{\frac {\partial ^{2}F}{\partial v\partial v'}}{\frac {{\text{d}}v}{{\text{d}}u}}+{\frac {\partial ^{2}F}{\partial u\partial v'}}-{\frac {\partial F}{\partial v}}=0$. $\qquad {\text{[2}}^{\text{b}}{\text{]}}$

第 89 條.
在微分方程理論中，已知任何形式為 [$2^{\text{b}}$] 的微分方程都可以用獨立變數 $u$ 的冪級數形式進行積分。

作為一個特例，我們有以下情況：

假設 1) *要形成的冪級數所代表的曲線在初始點處，我們有*

$u=0$，$v=b_{0}$，

其中 $b_{0}$ 是一個任意常數；

2) 曲線在初始點的方向由任意常數確定

${\frac {{\text{d}}v}{{\text{d}}u}}=v_{0}'$;

那麼，當 $u$ 的值足夠小時，$v$ 可以用冪級數表示。

$v=b_{0}+v_{0}'u+\cdots$, $\qquad {\text{[9]}}$

我們假設 $F_{1}$ 在初始點 $(0,b_{0})$ 不為零。

$v$ 在位置 $(0,b_{0},v_{0}')$ 的二階及更高階導數都可以從微分方程 [$2^{\text{b}}$] 推匯出來。因此，在 [9] 中，我們有 $v$ 是一個關於 $u$ 的冪級數，其係數除了每個問題中所含的常數外，還包含兩個任意常數 $b_{0}$ 和 $v_{0}'$，它們在不同的曲線之間會發生變化。

第 90 條.
如果將方程 [9] 中給出的 $v$ 的表示式代入公式 [3]，我們有 $x$ 和 $y$ 用 $u$ 表示。在這些表示式中，出現了常數 $g$，$g'$，$h$，$h'$，它們依賴於 $u$ 以及 $u$，$v$ 座標系的原點座標 $a$，$b$ 以及兩個積分常數 $b_{0}$ 和 $v_{0}'$，在第 89 條中定義。後兩個常數在不同的曲線之間是不同的。在這些公式中，就像在第 89 條中一樣，我們只能將小值賦給 $u$。

然而，我們知道，正如函式論中所看到的那樣，如果一條曲線只在很小的一部分被給出，那麼它的延續就被完全確定了。因此，我們只需要知道曲線在無限小的 $u$ 中的軌跡，就能隨意跟蹤它的軌跡。

曲線的座標 $x$，$y$ 可以表示為 $t$ 和兩個任意常數 $\alpha$ 和 $\beta$ 的函式。代替 $u$，我們可以引入另一個量的一個任意函式，只要這個量在曲線從起點到終點遍歷時以連續方式增加。正如已經提到的，積分的兩個常數在不同的曲線之間變化。如果我們適當地確定這些常數，我們可以迫使滿足微分方程 $G=0$ 的曲線透過兩個指定的點。

透過這種方式，我們清楚地瞭解了給出 $x$ 和 $y$ 的解析表示式的推導方式；一般來說，從方程 $G=0$ 中可以找到 $x$ 和 $y$，形式如下：

$x=\phi (t,\alpha ,\beta )$，$y=\psi (t,\alpha ,\beta )$。 $\qquad {\text{[10]}}$

同時可以看到，至少在一定程度上，$x$ 和 $y$ 是 $t$ 和兩個積分常數 $\alpha$ 和 $\beta$ 的單值正則函式，因此最終我們也可以對這兩個常數進行微分。

第 91 條.
在與第 89、90 條中所述內容相關的方面，這裡似乎需要考慮一個例外情況，即 $G=0$ 中的例外情況，即：

${\frac {\partial ^{2}f}{\partial v'^{2}}}=F_{1}={\frac {\partial ^{2}F}{\partial x'^{2}}}\sin ^{2}(\lambda )-2{\frac {\partial ^{2}f}{\partial x'\partial y'}}\sin(\lambda )\cos(\lambda )+{\frac {\partial ^{2}F}{\partial y'^{2}}}\cos ^{2}(\lambda )\qquad {\text{[8]}}$

等於曲線原點 $(y=0,v-b_{0})$ 為零，該曲線滿足方程 $G=0$.

我們將看到這只是一個特例，透過證明以下內容：

如果我們在點 $(u=0,v=b_{0})$ 周圍畫一個小圓，那麼這個圓可以被分成若干扇形，使得在每個扇形內 ${\frac {\partial ^{2}f}{\partial v'^{2}}}$ 不等於零。因為我們可以把圍繞初始點 $(u=0,v=b_{0})$ 的足夠小的圓的半徑視為該曲線的初始方向。如果對於 $v$ 我們在 [8] 中寫出 [9] 中給出的冪級數，我們有，透過置 $F_{1}=0$，一個用來確定 $v_{0}'$ 的方程，也就是固定初始方向的量。這個方程要麼沒有實根，那麼將不存在從點 $(u=0,v-b_{0})$ 出發的曲線，要麼 $F_{1}$ 對於單個 $v_{0}'$ 消失，那麼半徑確定了不同的扇形。在這些扇形內，可以從點 $(u=0,v-b_{0})$ 沿各個方向畫出曲線，其中 $F_{1}$ 不為零。因此，人們總是可以為 $v_{0}'$ 指定限制，在這些限制內，滿足方程 $G=0$ 並從點 $(u=0,v-b_{0})$ 出發的曲線，在原點至少有一個 $F_{1}$ 不為零。

第 92 條.
最後我們將證明，從同一點 $(u=0,v-b_{0})$ 出發的，滿足方程 $G=0$ 的曲線，在其初始點完全彼此分離。

如果我們在點 $(u=0,v=b_{0})$ 周圍畫一個小圓，那麼在其邊緣上，我們就可以很容易地確定點 $u$，$v$，它被其中一條曲線所截。假設 $\rho$ 是小圓的半徑，那麼

$u^{2}+(v-b_{0})^{2}=\rho ^{2}$。 $\qquad {\text{[11]}}$

將 [9] 中的冪級數代入 $v$，我們得到

$\rho ^{2}=(1+v_{0}'^{2})u^{2}+C_{3}u^{3}+\cdots$,

或者

$\rho ={\sqrt {1+v_{0}'^{2}}}u+(u)_{2}+\cdots$.

我們可以將這個級數反轉，得到 $u$ 作為 $\rho$ 的函式，因此

$u={\frac {1}{\sqrt {1+v_{0}'^{2}}}}\rho +(\rho )_{2}'+\cdots \qquad {\text{[12.1]}}$

因此

$v-b_{0}={\frac {v_{0}'}{\sqrt {1+v_{0}'^{2}}}}\rho +(\rho )_{2}''+\cdots \qquad {\text{[12.2]}}$

這些級數對於所有在一定極限$\rho _{0}$內的$\rho$都是收斂的，因此$u$和$v$，即在半徑為$\rho$的圓周上確定點的座標，對於所有$\rho <\rho _{0}$的值都是唯一確定的。因此，至少在開始時，屬於扇形的曲線實際上完全彼此分離。

第 93 條.
微分方程$G=0$的形式，其中$s$被引入作為自變數而不是$t$。 如果我們引入另一個變數$\tau$，代替$t$，並令$t$等於$\tau$的函式，我們得到相同的微分方程$G=0$。通常情況下，將弧長$s$作為自變數是有利的。

由於（第 68 條）函式$F$關於其第三個和第四個引數的導數是保持不變的，我們有（在第 68 條的公式中寫$k={\frac {1}{\sqrt {x'^{2}+y'^{2}}}}={\frac {{\text{d}}t}{{\text{d}}s}}$)

${\frac {\partial }{\partial x'}}F(x,y,x',y,)={\frac {\partial }{\partial \left({\frac {{\text{d}}x}{{\text{d}}s}}\right)}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

${\frac {\partial }{\partial y'}}F(x,y,x',y,)={\frac {\partial }{\partial \left({\frac {{\text{d}}y}{{\text{d}}s}}\right)}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

由此可見，${\frac {\partial F}{\partial x'}}$，${\frac {\partial F}{\partial y'}}$ 與表達 $y$ 和 $y$ 為 $t$ 的函式的方式無關，而只取決於曲線上該點的座標以及該點切線的方向。我們立即得到

${\frac {\partial ^{2}F}{\partial x'\partial y'}}={\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right){\frac {1}{\frac {{\text{d}}s}{{\text{d}}t}}}$;

由於

$F_{1}=-{\frac {1}{x'y'}}{\frac {\partial ^{2}F(x,y,x',y')}{\partial x'\partial y'}}$,

因此，我們得到

$F_{1}\left({\frac {{\text{d}}s}{{\text{d}}t}}\right)^{3}=-{\frac {1}{{\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}y}{{\text{d}}s}}}}{\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

如果我們進一步寫成

${\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=-{\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}y}{{\text{d}}s}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

我們有

$F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)\left({\frac {{\text{d}}s}{{\text{d}}t}}\right)^{3}=F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

因此方程$G=0$ 變為

${\frac {\partial ^{2}}{\partial x\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)-{\frac {\partial ^{2}}{\partial y\partial {\frac {{\text{d}}x}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)+\left({\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}-{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}\right)F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=0$.

第 94 條.
從上面的等式，$x$ 和 $y$ 關於 $s$ 的二階及更高階導數可以明確地用 $x$,$x$,${\frac {{\text{d}}x}{{\text{d}}s}}$,${\frac {{\text{d}}y}{{\text{d}}s}}$ 表示。

因為，從關係

$\left({\frac {{\text{d}}x}{{\text{d}}s}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}s}}\right)^{2}=1$,

可以推匯出，透過微分，得到

${\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}+{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}=0$. $\qquad {\text{[i]}}$

為了簡便，我們寫成

${\frac {\partial ^{2}}{\partial x\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)-{\frac {\partial ^{2}}{\partial y\partial {\frac {{\text{d}}x}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

我們可以將上一篇文章中的微分方程寫成以下形式：

$F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)\left({\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}-{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}\right)=H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$

藉助[i]，我們有

${\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)={\frac {{\text{d}}y}{{\text{d}}s}}H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$, ${\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=-{\frac {{\text{d}}y}{{\text{d}}s}}H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$. $\qquad {\text{[ii]}}$

無需進一步解釋即可說明如何從這些關係中表達 $x$ 和 $y$ 關於 $s$ 的三階及更高階導數，用 $x$， $y$， ${\frac {{\text{d}}x}{{\text{d}}s}}$ 和 ${\frac {{\text{d}}y}{{\text{d}}s}}$ 表示。

第 95 條.
因此，如果 $F_{1}$ 處處不為零，並且與 $H$ 一樣，是其自變數的連續函式，並且如果 $H$ 從不趨於無窮大（參見第 149 條），那麼，${\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}$ 和 ${\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}$ 從不趨於無窮大，並且也是弧長的連續函式。

由此可見，曲線在所討論的區間內沒有奇點，曲率也從不趨於無窮大。這可以透過以下方式證明：假設曲線上一點 $x_{0}$，$y_{0}$ 對應於 $s$ 的值 $s_{0}$，那麼根據上一條中方程 [ii]，該點附近曲線的方程可以表示為

$x=x_{0}+A(s-s_{0})^{\mu }+\cdots$,

$y=y_{0}+B(s-s_{0})^{\mu }+\cdots$,

其中常數 $A$ 和 $B$ 不會同時消失。當從這些方程中推匯出的 ${\frac {{\text{d}}x}{{\text{d}}s}}$ 和 ${\frac {{\text{d}}y}{{\text{d}}s}}$ 的值被代入

$\left({\frac {{\text{d}}x}{{\text{d}}s}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}s}}\right)^{2}=1$,

因此，我們得到

$1=\mu ^{2}(A^{2}+B^{2})(s-s_{0})^{2\mu -2}+A_{1}(s-s_{0})^{2\mu -3}+\cdots$,

由於該方程對於 $x_{0}$，$y_{0}$ 鄰域中的所有點都成立，可以看出

$A_{1}=A_{2}=\cdots =0$,

並且進一步可以看出

$\mu =1$，$A^{2}+B^{2}=1$。

因此，曲線位於 $x_{0}$，$y_{0}$ 鄰域中的每個點的座標都可以用正則函式表示

$x=x_{0}+A(s-s_{0})+\cdots$,

$y=y_{0}+B(s-s_{0})+\cdots$,

其中 $A$ 和 $B$ 不會同時消失。由於這對每個點 $x_{0}$，$y_{0}$ 都成立，因此曲線沒有奇點。因此，$x'$ 和 $y'$ 不會同時消失。