變分法/第十二章

第十二章：存在最大值或最小值的第四個也是最後一個條件，以及證明給定條件的充分性。

• 153 從前一章繼續討論場的概念。
• 154 函式${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})$。
• 155 函式${\mathcal {E}}$ 必須對曲線的每個點都具有相同的符號。
• 156 上述條件的充分性。
• 157 函式${\mathcal {E}}$ 的另一種形式。
• 158 另一種形式。
• 159，160 函式${\mathcal {E}}$ 和$F_{1}$ 的符號。
• 161 對第 156 條中給定條件的充分性的另一個證明。
• 162 函式${\mathcal {E}}$ 不能在給定場中的整條曲線上為零。
• 163 共軛點的包絡線。
• 164 曲線可以由有限數量的規則軌跡組成。
• 165 軌跡不規則的情況。
• 166 積分學中的推廣。
• 167，168，169，170，171，172 應用於前面已經考慮過的四個問題。
• 173 當$F(x,y,x',y')$ 是$x'$ 和$y'$ 的有理函式時，積分既不存在最大值也不存在最小值。
• 174 總體概述。
• 175 擴充套件和推廣：除了在兩個變數的域中確定第一類結構外，可能還需要在$n$ 個量的域中確定第一類結構。
• 176 當變數之間存在條件方程時。
• 177 當出現二階及更高階導數時。
• 178 變分法應用於更高階結構的確定。極小曲面。

第 153 條.
在前一章中，我們考慮了具有相同初始點$A$並滿足微分方程$G=0$ 的曲線族。它們在初始方向上彼此偏差很小。我們看到，這些曲線再次相交，僅在與$A$ 共軛的點的鄰域附近。在與$A$ 共軛的點之前，位於這些曲線上的所有點都形成一個連通的表面部分；也就是說，如果$P_{1}$ 是屬於這組點的點，則可以在$P_{1}$ 周圍描述一個邊界，使得該邊界內的所有點也屬於這組點。

因為，設

$x=\phi (t,\alpha ,\beta )\qquad y=\psi (t,\alpha ,\beta )$

是給定曲線方程，滿足$G=0$，且該曲線上一點的座標為

$x_{1}=\phi (t_{1},\alpha ,\beta )\qquad y_{1}=\psi (t_{1},\alpha ,\beta )$

此外，設$x_{1}+\xi ,y_{1}+\eta$ 為另一點的座標$P_{2}$，該點位於$P_{1},$ 的鄰域內，因此 $\xi ,\eta$ 是任意小的量。

然後我們可以在$A$和$P_{2}$之間畫一條滿足微分方程$G=0$的曲線（第151條），如果我們可以確定四個量$\tau ,\tau ',\alpha ',\beta '$ 作為$\xi ,\eta$ 的冪級數，使得以下方程成立

${\begin{aligned}0&=\phi '(t_{0})\tau '+\phi _{1}(t_{0})\alpha '+\phi _{2}(t_{0})\beta '+(\tau ',\alpha ',\beta ')_{2}\\0&=\psi '(t_{0})\tau '+\psi _{1}(t_{0})\alpha '+\psi _{2}(t_{0})\beta '+(\tau ',\alpha ',\beta ')_{2}\\\xi &=\phi '(t_{1})\tau '+\phi _{1}(t_{1})\alpha '+\phi _{2}(t_{1})\beta '+(\tau ,\alpha ',\beta ')_{2}\\\eta &=\psi '(t_{1})\tau '+\psi _{1}(t_{1})\alpha '+\psi _{2}(t_{1})\beta '+(\tau ,\alpha ',\beta ')_{2}\end{aligned}}$

由於這些方程式的行列式（第151條）為 $-\Theta (t_{1},t_{0})$ 且不等於零，點 $t_{1}$ 與 $t_{0}$ 不是共軛的，因此，量 $\tau ,\tau ',\alpha ',\beta '$ 可以展開成關於 $\xi ,\eta$ 的冪級數，這些級數在這些量的較小值時收斂。

因此，可以畫出一條透過 $A$ 和 $P_{2}$ 的曲線，該曲線滿足微分方程 $G=0$，並且這條曲線將鄰近第一條曲線，並且如果 $\xi ,\eta$，因此 $\tau ,\tau ',\alpha ',\beta '$ 也足夠小，在方向上儘可能地偏離其初始方向。

如果我們對曲線$AP_{2}$形成行列式，當該行列式等於零時，就是確定與$A$共軛點的方程，可以看出，這個行列式也可以展開成$\xi ,\eta$的冪級數，當$\xi =\eta =0$時，它變為$-\Theta (t_{1},t_{0})$。函式$\Theta (t_{1},t_{0})$當對$\xi ,\eta$賦予足夠小的值時，不等於零。因此，在區間$AP_{2}$內，不存在與$A$共軛的點。

因此，我們可以用一個狹窄的表面區域包圍原始曲線兩個共軛點之間的區間，這個表面區域的性質是，可以從點$A$到其中的任何一點畫出一條且僅有一條曲線，這條曲線滿足微分方程$G=0$，並且鄰近第一條曲線，其初始方向僅略微偏離第一條曲線。

第154條

.
設曲線$P_{0}P_{1}$的一段滿足微分方程$G=0$，其性質為，在其上任何一點都不滿足$F_{1}=0$或$\infty$，並假設與$P_{0}$共軛的點不位於$P_{1}$之前。在$P_{0}$和$P_{1}$之間取任意一點$P_{2}$，並過$P_{2}$作一條正則曲線。 在這條曲線上，我們選擇一個點$P_{3}$，使其非常接近$P_{2}$，以便可以過$P_{0}$和$P_{3}$作一條滿足微分方程$G=0$的曲線，並且完全位於上述定義的曲面帶內。讓我們考慮當積分沿著$P_{0}P_{3}+P_{3}P_{2}$而不是沿著$P_{0}P_{2}$時積分的變化。我們可以用$I$表示沿著滿足微分方程的曲線進行的積分，用${\bar {I}}$表示沿著任意曲線進行的積分，並透過新增下標來表示積分的方向。因此，我們必須計算表示式

$\Delta I=I_{03}+{\bar {I}}_{32}-I_{02}$

或者

$\Delta I=\left(\int _{\overline {P_{0}P_{3}}}F{\text{d}}t-\int _{\overline {P_{0}P_{2}}}F{\text{d}}t\right)+\int _{\overline {P_{0}P_{2}}}F{\text{d}}t$

一個表示式（第79條）

$=\epsilon \left(\int _{\overline {P_{0}P_{2}}}Gw{\text{d}}s+\left[\xi {\frac {\partial F}{\partial x'}}+\eta {\frac {\partial F}{\partial y'}}\right]^{t_{2}}\right)+(\epsilon ^{2})+\int _{\overline {P_{0}P_{2}}}F{\text{d}}t$

其中$\xi ,\eta$是在從$P_{2}$到$P_{3}$的方向上測量的。

在點$P_{2}$以及沿著曲線$P_{3}P_{2}$的方向$P_{3}P_{2}$，我們有

$\epsilon \xi =-{\bar {x}}_{2}'{\text{d}}{\bar {t}}+({\text{d}}{\bar {t}})^{2}\qquad \epsilon \eta =-{\bar {y}}_{2}'{\text{d}}{\bar {t}}+({\text{d}}{\bar {t}})^{2}$

${\text{d}}{\bar {t}}$ 表示該微分是相對於曲線 $P_{3}P_{2}$ 進行的。

如果我們考慮 $F$ 中的引數表示為沿曲線 $P_{3}P_{2}$ 上 ${\bar {t}}$ 的函式，則可以得出

$\int _{\overline {P_{0}P_{2}}}F{\text{d}}t=F(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}'){\text{d}}{\bar {t}}+({\text{d}}{\bar {t}})^{2}$

因此，在點 $P_{2}$ 處，它是曲線 $P_{0}P_{1}$ 上的任意一點，我們有

$\Delta I=\left(F(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')-\left[{\bar {x}}_{2}'{\frac {\partial }{\partial x_{2}'}}F(x_{2},y_{2},x_{2}',y_{2}')+{\bar {y}}_{2}'{\frac {\partial }{\partial y_{2}'}}F(x_{2},y_{2},x_{2}',y_{2}')\right]\right){\text{d}}{\bar {t}}+({\text{d}}{\bar {t}})^{2}\qquad$(a)

函式 $F$ 關於其第三和第四個引數是一階齊次的（第 68 條），因此（參見第 72 條）

$F(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')={\bar {x}}_{2}'F^{(1)}(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')+{\bar {y}}_{2}'F^{(2)}(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')$

我們用 ${\mathcal {E}}(x,y,x',y',{\bar {x}}',{\bar {y}}')$ 表示以下表達式。

$1)\qquad {\mathcal {E}}(x,y,x',y',{\bar {x}}',{\bar {y}}')={\bar {x}}'{\big (}F^{(1)}(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')-F^{(1)}(x_{2},y_{2},x_{2}',y_{2}'){\big )}+{\bar {y}}'{\big (}F^{(2)}(x_{2},y_{2},{\bar {x}}_{2}',{\bar {y}}_{2}')-F^{(2)}(x_{2},y_{2},x_{2}',y_{2}'){\big )}$

因此，在點 $P2$，可以得出

$\Delta I={\mathcal {E}}(x,y,x',y',{\bar {x}}',{\bar {y}}'){\text{d}}{\bar {t}}+({\text{d}}{\bar {t}})^{2}$

當在函式${\mathcal {E}}$中，我們已經將屬於點$P_{2}$的那些值代入了引數。曲線$P_{0}P_{2}$在$P$處的方向餘弦用

$p_{2}={\frac {x_{2}'}{\sqrt {x_{2}'^{2}+x_{2}'^{2}}}}\qquad {\text{and}}\qquad q_{2}={\frac {y_{2}'}{\sqrt {x_{2}'^{2}+x_{2}'^{2}}}}$

而曲線$P_{3}P_{2}$在$P_{2}$處的方向餘弦用${\bar {p}}_{2}$和${\bar {q}}_{2}$表示。從定義${\mathcal {E}}$的公式的右側（參見第68條）可以明顯看出

${\frac {{\mathcal {E}}(x,y,x',y',{\bar {x}}',{\bar {y}}')}{\sqrt {{\bar {x}}_{2}'^{2}+{\bar {y}}_{2}'^{2}}}}={\mathcal {E}}(x,y,p,q,{\bar {q}},{\bar {q}})$

第155條.
如果我們進一步用$\sigma$表示弧$P_{3}P_{2}$的微分，那麼我們最終得到

$2)\qquad \Delta I={\mathcal {E}}(x,y,p,q,{\bar {p}}',{\bar {q}})\sigma +(\sigma )^{2}$

因此，如果我們取$\sigma$ 足夠小；也就是說，如果我們選擇點$P_{3}$ 非常接近$P_{2}$，那麼我們總是可以使積分的變化與函式${\mathcal {E}}$的變化具有相同的符號。

點$P_{2}$ 是曲線$P_{0}P_{1}$ 上的任意一點，而$P_{2}P_{3}$ 也表示任意方向。

由此可見，如果對於任何一點$P_{2}$ 和$P_{2}$ 處的任何方向，函式${\mathcal {E}}$ 均為負，而對於任何其他點和方向均為正，則給定曲線可以以積分變化有時為正，有時為負的方式變化。因此，我們有以下定理：

如果在滿足微分方程$G=0$的曲線$P_{0}P_{1}$ 上的積分要取得最大值或最小值，則函式${\mathcal {E}}$ 必須對曲線的每個點以及曲線每個點的任何方向都具有相同的符號，並且對於最大值此符號必須為負，對於最小值必須為正。

第 156 條.
上述條件足以確保最大值或最小值的存在，可以如下證明：令$P_{0}(I)P_{1}$ 為滿足已建立的四個條件（並在第 174 條中概括）的曲線，並令$P_{0}(II)P_{1}$ 為位於曲線$P_{0}(I)P_{1}$ 周圍場的任何任意曲線。它僅受以下條件的約束：它必須是一條規則曲線，並且完全位於給定場中。

透過改變引數$\alpha$和$\beta$，我們可以構建一個曲線系統，使其彼此無限接近，所有曲線都滿足微分方程$G=0$。這些曲線與曲線$P_{0}(II)P_{1}$相交於兩點（或可能更多）。它們不與曲線$P_{0}(I)P_{1}$相交，也不在所討論的域內彼此相交。函式${\mathcal {E}}$必須在這些曲線上的每個點上都具有與它在曲線$P_{0}(I)P_{1}$上相同的符號。因為，取任意一點$P$在這些曲線中的任意一條上。那麼在曲線$P_{0}(I)P_{1}$上存在一個點，對於該點，量$x,y,p,q$僅略微不同於屬於點$P$的量，因此${\mathcal {E}}$對這兩個點具有相同的符號。

現在考慮當我們從$P_{0}(I)P_{1}$ 變到 $P_{0}P_{2}P_{3}P_{1}$，以及從 $P_{0}P_{2}P_{3}P_{1}$ 變到 $P_{0}P_{4}P_{5}P_{1}$ 等積分的變化。正如我們在前一篇文章中所看到的，從 $P_{0}(I)P_{1}$ 變到 $P_{0}P_{2}P_{3}P_{1}$ 引起的變分。

$=\int _{t_{0}}^{t_{2}}F{\text{d}}t+\epsilon \left[{\frac {\partial F}{\partial x'}}\xi +{\frac {\partial F}{\partial y'}}\eta \right]_{t_{2}}^{t_{3}}+\int _{t_{3}}^{t_{1}}F{\text{d}}t$

$=\int _{t_{0}}^{t_{2}}F{\text{d}}t-\left[{\bar {p}}{\frac {\partial F}{\partial x'}}+{\bar {q}}{\frac {\partial F}{\partial y'}}\right]^{t_{2}}\sigma +\int _{t_{3}}^{t_{1}}F{\text{d}}t-\left[{\bar {p}}{\frac {\partial F}{\partial x'}}+{\bar {q}}{\frac {\partial F}{\partial y'}}\right]^{t_{3}}\sigma$

${\bar {p}},{\bar {q}}$ 是曲線 $P_{0}(II)P_{1}$ 在點 $P_{2}$ 和 $P_{3}$ 處的切線的方向餘弦，我們注意到，在這些點上，它們具有相反的符號。

如果我們用曲線本身表示沿曲線的積分，則可以立即看出這些積分的變化可以用以下公式表示：

$P_{0}P_{2}P_{3}1P_{1}-P_{0}(I)P_{1}=[{\mathcal {E}}]^{t_{0}}\sigma +[{\mathcal {E}}]^{t_{1}}\sigma +(\sigma )^{2}$

其中，第一個是$P_{0}$到$P_{2}$的長度，第二個是$P_{3}$到$P_{1}$的長度。

類似地，沿以下路徑積分的差異為：

$P_{0}P_{4}P_{5}1P_{1}-P_{0}P_{2}P_{3}P_{1}=[{\mathcal {E}}]^{t_{2}}\sigma +[{\mathcal {E}}]^{t_{3}}\sigma +(\sigma )^{2}$

$P_{0}P_{6}P_{7}1P_{1}-P_{0}P_{4}P_{5}P_{1}=[{\mathcal {E}}]^{t_{4}}\sigma +[{\mathcal {E}}]^{t_{5}}\sigma +(\sigma )^{2}$

$...................................$

$P_{0}P_{2\nu }P_{2\nu +1}1P_{1}-P_{0}P_{2\nu -2}P_{2\nu -1}P_{1}=[{\mathcal {E}}]^{t_{2\nu -2}}\sigma +[{\mathcal {E}}]^{t_{2\nu -1}}\sigma +(\sigma )^{2}$

$P_{0}(II)P_{1}-P_{0}P_{2\nu }P_{2\nu +1}P_{1}=[{\mathcal {E}}]^{t_{2\nu }}\sigma +[{\mathcal {E}}]^{t_{2\nu +1}}\sigma +(\sigma )^{2}$

將這些結果加在一起，我們得到了沿著以下路徑積分的差值：

$P_{0}(II)P_{1}-P_{0}(II)P_{1}=\int _{P_{0}(II)P_{1}}{\mathcal {E}}\sigma +(\sigma )^{2}$

$\sigma$ 是沿著曲線 $P_{0}(I)P_{1}$ 的弧微分。這驗證了上一節末尾陳述的定理。

我們還看到，如果我們沒有確保沒有中間曲線相交，則 $\sigma$ 的符號不會都相同，因此所有這些 $\sigma$ 的總和將不會構成曲線 $P_{)}(II)P_{1}$。

第 157 條.
函式 ${\mathcal {E}}$的另一種形式。

我們在積分學中看到過

$f(p_{1},q_{1})-f(p_{0},q_{0})=\int _{p_{0},q_{0}}^{p_{1},q_{1}}{\text{d}}f(p,q)$

$\qquad =\int _{p_{0},q_{0}}^{p_{1},q_{1}}\left({\frac {\partial f(p,q)}{\partial p}}{\text{d}}p+{\frac {\partial f(p,q)}{\partial q}}{\text{d}}q\right)$

$\qquad =\int _{k=0}^{k=1}{\big (}f^{(1)}[p_{0}+k(p_{1}-p_{0}),q_{0}+k(q_{1}-q_{0})](p_{1}-p_{0})+f^{(2)}[p_{0}+k(p_{1}-p_{0}),q_{0}+k(q_{1}-q_{0})](q_{1}-q_{0}){\big )}{\text{d}}k$

因此，如果我們寫成

$p_{k}=p+k({\bar {p}}-p)=(1-k)p+k{\bar {p}}$

$q_{k}=q+k({\bar {q}}-q)=(1-k)q+k{\bar {q}}$

可以看出

$F^{(1)}(x,y,{\bar {p}},{\bar {q}})-F^{(1)}(x,y,p,q)=\int _{k=0}^{k=1}{\big (}F^{(11)}(x,y,p_{k},q_{k})({\bar {p}}-p)+F^{(12)}(x,y,p_{k},q_{k})({\bar {q}}-q){\big )}{\text{d}}k$

$F^{(2)}(x,y,{\bar {p}},{\bar {q}})-F^{(2)}(x,y,p,q)=\int _{k=0}^{k=1}{\big (}F^{(21)}(x,y,p_{k},q_{k})({\bar {p}}-p)+F^{(22)}(x,y,p_{k},q_{k})({\bar {q}}-q){\big )}{\text{d}}k$

注意（參見第73條）

$F^{(11)}=q_{k}^{2}F_{1}\qquad F^{(12)}=-p_{k}q_{k}F_{1}\qquad F^{(22)}=p_{k}^{2}F_{1}$

並且進一步地，$F^{(12)}=F^{(21)}$。

透過將這些值代入上述表示式，進而將所得結果代入${\mathcal {E}}$的表示式中，我們得到

${\mathcal {E}}(x,y,p,q,{\bar {p}}{\bar {q}})={\bar {p}}[F^{(1)}(x,y,{\bar {p}},{\bar {q}})-F^{(1)}(x,y,p,q)]+{\bar {q}}[F^{(2)}(x,y,{\bar {p}},{\bar {q}})-F^{(2)}(x,y,p,q)]$

$\qquad =\int _{k=0}^{k=1}F_{1}(x,y,p_{k},q_{k}){\big (}[q_{k}({\bar {p}}-p)-p_{k}({\bar {q}}-q)]q_{k}{\bar {p}}+[-q_{k}({\bar {p}}-p)+p_{k}({\bar {q}}-q)]p_{k}{\bar {q}}{\big )}{\text{d}}k$

方括號中的表示式為

$(q_{k}{\bar {p}}-p_{k}{\bar {q}})[q_{k}({\bar {p}}-p)-p_{k}({\bar {q}}-q)]=(1-k)(q{\bar {p}}-p{\bar {q}})^{2}$

因此

$3)\qquad {\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=(q{\bar {p}}-p{\bar {q}})^{2}\int _{k=0}^{k=1}F_{1}(x,y,p_{k},q_{k}){\text{d}}k$

以定積分形式表達${\mathcal {E}}$的表示式是有缺陷的，因為它只有當$F_{1}$對於$p_{k}$和$q_{k}$的所有取值都保持有限，且$k$在0到1之間變化時才具有意義。例如，如果$k=1/2$，則$p_{1/2}=p+({\bar {p}}-p)/2=(p+{\bar {p}})/2$，並且如果${\bar {p}}=-p$，則$p_{1/2}=0$；同理，對於$k=1/2$和${\bar {q}}=-q$，則也有$q_{1/2}=0$。這兩個引數都為零時，$F_{1}$變為無窮大（參見第73條）。此外，如果兩個方向$p,q$和${\bar {p}},{\bar {q}}$重合，則${\mathcal {E}}$變為二階零。

如果$OP$ 和 $O{\bar {P}}$ 是分量分別為 $p,q$ 和 ${\bar {p}},{\bar {q}}$ 的單位長度向量，則當 $P'$沿著直線 $P{\bar {P}}$ 運動時，$OP'$ 的分量為 $p_{k},q_{k},k$，其中k在0到1之間變化。

第158條.
魏爾斯特拉斯給出了表示式 ${\mathcal {E}}$ 的另一種形式，他透過沿著圓弧而不是沿著直線 $P{\bar {P}}$ 進行積分，避免了上述缺陷。如果我們沿著半徑為1的圓弧從點 $P$ 積分到點 ${\bar {P}}$，我們就得到了 ${\mathcal {E}}$ 的一個普遍適用的表示式。

我們像以前一樣，如果 $POX=\tau$，${\bar {P}}OX={\bar {\tau }}$，$\omega ={\bar {\tau }}-\tau ({\text{mod }}2\pi )$，並且 $-\pi \leq \omega \leq =\pi$。

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})={\bar {p}}[F^{(1)}(x,y,{\bar {p}},{\bar {q}})-F^{(1)}(x,y,p,q)]+{\bar {q}}[F^{(2)}(x,y,{\bar {p}},{\bar {q}})-F^{(2)}(x,y,p,q)]$

$=\cos {\bar {\tau }}[F^{(1)}(x,y,\cos {\bar {\tau }},\sin {\bar {\tau }})-F^{(1)}(x,y,\cos \tau ,\sin \tau )]+\sin {\bar {\tau }}[F^{(2)}(x,y,\cos {\bar {\tau }},\sin {\bar {\tau }})-F^{(2)}(x,y,\cos \tau ,\sin \tau )]$

$=\cos {\bar {\tau }}\int _{\lambda =0}^{\lambda =\omega }{\text{d}}_{\lambda }F^{(1)}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]+\sin {\bar {\tau }}\int _{\lambda =0}^{\lambda =\omega }{\text{d}}_{\lambda }F^{(2)}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]$

但是，如果$F^{(1)}$表示$F$對其第三個引數的導數，等等，

${\text{d}}_{\lambda }F^{(1)}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]$

$\qquad =[F_{\cos ,\cos }^{(11)}\sin(\tau +\lambda )+F_{\cos ,\sin }^{(12)}\cos(\tau +\lambda )]{\text{d}}\lambda$

$\qquad =[-\sin ^{3}(\tau +\lambda )-\sin(\tau +\lambda )\cos ^{2}(\tau +\lambda )]F_{1}{\text{d}}\lambda$

$\qquad =-\sin(\tau +\lambda )F_{1}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]{\text{d}}\lambda$

類似地，

${\text{d}}_{\lambda }F^{(2)}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]=\cos(\tau +\lambda )F_{1}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]{\text{d}}\lambda$

因此，可以得出

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=\int _{\lambda =0}^{\lambda =\omega }[-\cos {\bar {\tau }}\sin(\tau +\lambda )+\sin {\bar {\tau }}\cos(\tau +\lambda )]F_{1}{\text{d}}\lambda$

$\qquad =\int _{\lambda =0}^{\lambda =\omega }\sin({\bar {\tau }}-\tau -\lambda )F_{1}{\text{d}}\lambda =\int _{\lambda =0}^{\lambda =\omega }\sin(\omega -\lambda )F_{1}[x,t,\cos(\tau +\lambda ),\sin(\tau +\lambda )]{\text{d}}\lambda$

如果我們寫

$\omega -\lambda =\lambda '$

剛才寫的積分是

$\int _{\lambda '=0}^{\lambda '=\omega }\sin \lambda 'F_{1}[x,y,\cos({\bar {\tau }}-\lambda '),\sin({\bar {\tau }}-\lambda ')]{\text{d}}\lambda '=F_{1}[x,y,\cos({\bar {\tau }}-\lambda _{2}'),\sin({\bar {\tau }}-\lambda _{2}')]\int _{\lambda '=0}^{\lambda '=\omega }{\text{d}}~\cos \lambda '$

其中$\lambda _{2}'$ 是 0 和 $\omega$ 之間的中間值。

因此，我們最終得到

$4)\qquad {\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=(1-\cos \omega )F_{1}[x,y,cos({\bar {\tau }}-\lambda _{2}'),\sin({\bar {\tau }}\lambda _{2}')]$

如果 $F_{1}[x,y,cos({\bar {\tau }}-\lambda '),\sin({\bar {\tau }}\lambda _{'})]$ 在 0 到 $\omega$ 之間具有恆定的符號，則 ${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})$ 也具有此符號，因為 $\lambda _{2}'$ 是此區間內 $\lambda '$ 的值之一。

上述公式對於介於 $-\pi$ 和 $+\pi$ 之間的所有 $\omega$ 值都成立，並且由於 $\cos({\bar {\tau }}-\lambda _{2}')$ 和 $\sin({\bar {\tau }}-\lambda _{2}')$ 不會同時為零，因此可以看出

$F_{1}[x,y,\cos({\bar {\tau }}-\lambda _{2}'),\sin({\bar {\tau }}-\lambda _{2}')]\neq \infty$

因此，${\mathcal {E}}$ 的表示式 4 並不存在與前一篇文章中給出的表示式相同的缺陷。

第 159 條

.
對於曲線$\omega \neq 0$的任何位移，因此$1-\cos \omega$是一個正量。因此${\mathcal {E}}$與$F_{1}$具有相同的符號。如果經檢驗發現$F_{1}[x,y,\cos({\bar {\tau }}-\lambda ),\sin({\bar {\tau }}-\lambda )]$與$\cos({\bar {\tau }}-\lambda )$、$\sin({\bar {\tau }}-\lambda )$無關，在所討論的區間內曲線的每個點上始終具有相同的符號，那麼我們就可以確信積分存在最大值或最小值，而無需推導和檢查函式${\mathcal {E}}$。但是，透過這個過程，我們已經在沒有使用二次變分的情況下證明了函式$F_{1}(x,y,p,q)$在曲線上任何點上以及在該點曲線的切線的任何方向上都不會改變其符號。

第 160 條.
顯然，如果將$F_{1}$視為其第三和第四個自變數的函式，具有確定的符號，則${\mathcal {E}}$也具有相同的符號；但是，如果${\mathcal {E}}$保持確定的符號，$p$和$q$固定，而${\bar {p}}$和${\bar {q}}$發生變化，則$F_{1}$始終具有確定的符號並不一定成立。施瓦茨給出了以下示例來說明這一點。

令

$F(x,y,x',y')=\alpha {\sqrt {x'^{2}+y'^{2}}}+beta{\frac {x'y'^{2}}{x'^{2}+y'^{2}}}=(\alpha +\beta \cos \tau \sin ^{2}\tau ){\sqrt {x'^{2}+y'^{2}}}$

由此可得

$F_{1}(x,y,x',y')={\frac {\alpha }{(x'^{2}+y'^{2})^{3/2}}}+2\beta {\frac {x'(x'^{2}-3y'^{2})}{(x'^{2}+y'^{2})^{3}}}=(\alpha +2\beta \cos 3\tau ){\frac {1}{(x'^{2}+y'^{2})^{3/2}}}$

並且，由於 $x'^{2}+y'^{2}=\cos ^{2}\lambda +\sin ^{2}\lambda =1$,

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=\int _{\lambda =0}^{\lambda =\omega }\sin(\omega -\lambda )F_{1}[x,y,\cos(\tau +\lambda ),\sin(\tau +\lambda )]{\text{d}}\lambda$

$\qquad =\int _{\lambda =0}^{\lambda =\omega }\sin(\omega -\lambda )(\alpha +2\beta \cos 3\lambda ){\text{d}}\lambda$

這裡我們寫成 $\tau +\lambda =\lambda$ 或 $\tau =0$；也就是說，我們取 $X$-軸作為初始方向，由此測量 $\omega$。

注意到

$\sin(\omega +2\lambda )+\sin(\omega -4\lambda )=2\sin(\omega -\lambda )\cos 3\lambda$

可以看出

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=(1-\cos \omega )[\alpha +\beta (\cos \omega +\cos ^{2}\omega )]$

$\cos \omega +\cos ^{2}\omega$ 的最大值和最小值分別為 2 和 $-1/4$，對應的 $\omega$ 值分別為 0 和 $2\pi /3$。因此，如果我們令 $\alpha =l$ 且 $/beta=1$，則函式 ${\mathcal {E}}$ 的值介於

${\frac {3}{4}}(1-\cos \omega )~{\text{and}}~3(1-\cos \omega )$

之間，因此它僅當 $\omega =0$ 時才可能為零，並且永不為負。另一方面，$1+2\cos 3\tau$ 會反覆改變符號，例如，當 $\tau =40^{\circ }$ 時。

第 161 條.
第 155 條末尾給出的證明對於確定是否存在真正的最大值或最小值至關重要。第 156 條說明的該定理充分性的證明，由施瓦茨教授以稍微不同的形式給出。由於其重要性，我們補充另一個證明，摘自魏爾斯特拉斯的講義。

設$OO_{1}1$ 為滿足微分方程$G=0$ 的曲線，並設$0_{1}31$ 為場中任意曲線，如第 156 條所定義。設 3 為任意曲線上的任意一點，我們將其座標視為弧長$s$（而不是像以前一樣用$t$）的函式。點$O_{1}$ 取在 0 和 1 之間，以便曲線$0_{1}31$ 可以完全位於場內，因為場可能在 0 處終止於一點。從點 0 我們畫一條滿足微分方程$G=0$ 的曲線到 3。我們將積分和$I_{03}+{\bar {I}}_{31}$ 視為$s$ 的函式。我們將此函式記為$\int (s)$。此外，在任意曲線上取一點 2，位於點 3 的鄰域且在其之前。用一條滿足微分方程$G=0$ 的曲線連線點 0 和 2。那麼，如果我們將$s$ 的增量記為$\sigma$，可以看出

$5)\qquad \int (s-\sigma )-\int (s)=I_{02}+{\bar {I}}_{21}-I_{03}-{\bar {I}}_{31}=I_{02}-I_{03}+{\bar {I}}_{23}={\mathcal {E}}(x_{3},y_{3},p_{3},q_{3},{\bar {p}}_{3},{\bar {q}}_{3})\sigma +(\sigma )^{2}$

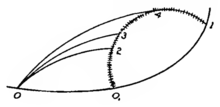
以同樣的方式，在任意曲線上取一點 4，緊接在點 3 之後，並用一條滿足微分方程$G=0$ 的曲線連線此點與點 0。那麼我們有

$6)\qquad \int (s-\sigma )-\int (s)=I_{04}-I_{03}-{\bar {I}}_{34}=-{\mathcal {E}}(x_{3},y_{3},p_{3},q_{3},{\bar {p}}_{3},{\bar {q}}_{3})\sigma +(\sigma )^{2}$

因此可以得出

$7)\qquad \lim _{\sigma =0}{\frac {\int (s-\sigma )-\int (s)}{-\sigma }}=\lim _{\sigma =0}{\frac {\int (s+\sigma )-\int (s)}{\sigma }}=-{\mathcal {E}}(x_{3},y_{3},p_{3},q_{3},{\bar {p}}_{3},{\bar {q}}_{3})$

也就是說，量$-{\mathcal {E}}(x_{3},y_{3},p_{3},q_{3},{\bar {p}}_{3},{\bar {q}}_{3})$是函式$\int (s)$在點3處的微商。

如果，那麼沿著曲線$O_{1}31$，函式${\mathcal {E}}$處處不為正，則當點3從$O_{1}$向點1滑動時，函式$\int (s)$連續減小。

現在，設取在點0附近的很靠近0的點$O_{1}$與該點重合；那麼我們可以說

如果函式${\mathcal {E}}$在任意曲線上都不為正，且在任意曲線031的每一點都不為零，則沿原曲線積分總是大於沿曲線031的積分；如果函式${\mathcal {E}}$不為負，且在曲線031的每一點都不為零，則沿原曲線01的積分總是小於沿任意曲線031的積分。

第162條.
現在我們還要看看函式${\mathcal {E}}$是否可能沿整個曲線031都等於零。從公式3)可以看出，只有當沿整個曲線滿足以下條件時，才有可能：

$(p{\bar {q}}-q{\bar {p}})^{2}=0{\text{ or }}p{\bar {q}}-q{\bar {p}}=0$

在這種情況下，每條滿足微分方程$G=0$的曲線03，在點3處與曲線031具有共同的切線。

我們將證明，由與點0共軛的點組成的曲線$MN$具有此性質，並且在由$MN$包圍的區域內，無法從0畫出具有此性質的任何其他曲線。換句話說，${\mathcal {E}}$沿曲線$MN$等於零，但對於在$MN$所包圍的區域內能夠畫出的任何其他曲線的全部點，都不等於零。

所有滿足微分方程$G=0$，且透過同一點，其初始方向彼此之間相差很小的曲線，可以用（第148條）以下形式表示：

$x=\phi (t,k)\qquad y=\psi (t,k)$

其中$k$的值在一定的範圍內。

每條曲線對應一個不同的$k$值。因此，如果我們固定一個$k$的值，並取第二個值$k+k'$，則對應於該值的曲線可以用以下方程表示。

$x+\xi =\phi (t+\tau ',k+k')\qquad y+\eta =\psi (t+\tau ',k+k')$

其中，相同的$t$值對應於兩條曲線的初始方向。

如果後一條曲線與前一條曲線相交，則必須有

$0=\phi '(t)\tau '+{\frac {\partial \phi }{\partial k}}k'+(\tau ',k')_{2}\qquad 0=\psi '(t)\tau '+{\frac {\partial \psi }{\partial k}}k'+(\tau ',k')_{2}$

剛剛寫出的方程中線性項的行列式，當等於零時，給出了確定與初始點共軛點的方程，即

$\phi '(t){\frac {\partial \psi }{\partial k}}-\psi '(t){\frac {\partial \phi }{\partial k}}=0$ \qquad (A)

該方程中大於$t$的值$t_{0}$的最小根，給出了屬於共軛點的$t$值。如果這個值是$t_{1}$，則該點的座標為

${\bar {x}}=\phi (t_{1},k)\qquad {\bar {y}}=\psi (t_{1},k)$

如果我們將$t_{1}$視為$k$的函式，該函式由方程(A)定義，並且如果我們給$k$一系列的值，則剛剛寫出的這兩個方程表示由與0共軛的點構成的曲線。

此曲線的切線的方向餘弦與下列量成比例 ${\frac {\partial {\bar {x}}}{\partial k}},{\frac {\partial {\bar {y}}}{\partial k}}$。但是我們也有

${\frac {\partial {\bar {x}}}{\partial k}}={\frac {\partial \phi (t_{1},k)}{\partial t_{1}}}{\frac {{\text{d}}t_{1}}{{\text{d}}k}}+{\frac {\partial \phi (t_{1},k)}{\partial k}}\qquad {\frac {\partial {\bar {y}}}{\partial k}}={\frac {\partial \psi (t_{1},k)}{\partial t_{1}}}{\frac {{\text{d}}t_{1}}{{\text{d}}k}}+{\frac {\partial \psi (t_{1},k)}{\partial k}}$

將第一個方程乘以 ${\frac {\partial \psi (t_{1},k)}{\partial t_{1}}}=\psi '(t_{1})$，然後從中減去第二個方程，在減之前將第二個方程乘以 ${\frac {\partial \phi (t_{1},k)}{\partial t_{1}}}=\phi '(t_{1})$。然後，藉助 (A)，我們有

$\phi '(t_{1}){\frac {{\text{d}}{\bar {y}}}{{\text{d}}k}}-\psi '(t_{1}){\frac {{\text{d}}{\bar {x}}}{{\text{d}}k}}=0$

由於 $\phi '(t_{1}),\psi '(t_{1})$ 與透過點 $t_{0}$ 和 $t_{1}$ 的曲線上一點 $t_{1}$ 的切線的方向餘弦成比例，且滿足微分方程 $G=0$，因此，根據上述方程，兩條曲線在點 $t_{1}$ 處的切線重合。 *因此，共軛點的軌跡是透過 0 且滿足微分方程 $G=0$ 的曲線的包絡。*

第 163 條

.
設${\bar {x}}=f(u)$ 和 ${\bar {y}}=g(u)$ 為任意曲線 031，該曲線透過點 0，且完全位於包絡線所包圍的區域內。此外，假設 031 在其整個範圍內不與任何透過 0 並滿足微分方程 $G=0$ 的曲線重合。然而，假設 031 被透過 0 並滿足微分方程 $G=0$ 的曲線所接觸。在接觸點，我們必須有

$\phi (t,k)=f(u)\qquad \psi (t,k)=g(u)$

以及

${\frac {\partial \phi }{\partial t}}{\frac {{\text{d}}g}{{\text{d}}u}}-{\frac {\partial \psi }{\partial t}}{\frac {{\text{d}}f}{{\text{d}}u}}=0$ \qquad (B)

屬於接觸點的 $t$ 和 $u$ 的值透過前兩個方程確定為 $k$ 的函式。

這些方程對於 $k$ 的足夠小的值成立，可以對 $k$ 求導，因此我們有

${\frac {\partial \phi }{\partial t}}{\frac {{\text{d}}t}{{\text{d}}k}}+{\frac {\partial \phi }{\partial k}}={\frac {{\text{d}}f}{{\text{d}}u}}{\frac {{\text{d}}u}{{\text{d}}k}}\qquad {\frac {\partial \psi }{\partial t}}{\frac {{\text{d}}t}{{\text{d}}k}}+{\frac {\partial \psi }{\partial k}}={\frac {{\text{d}}g}{{\text{d}}u}}{\frac {{\text{d}}u}{{\text{d}}k}}$

如果我們將第一個方程乘以 ${\frac {{\text{d}}g}{{\text{d}}u}}$，第二個方程乘以 $-{\frac {{\text{d}}f}{{\text{d}}u}}$，然後相加，利用 (B)，我們得到

${\frac {\partial \phi }{\partial k}}{\frac {{\text{d}}g}{{\text{d}}u}}-{\frac {\partial \psi }{\partial k}}{\frac {{\text{d}}f}{{\text{d}}u}}=0$

如果在這個方程和方程(B)之間消去 ${\frac {{\text{d}}g}{{\text{d}}u}}$ 和 ${\frac {{\text{d}}f}{{\text{d}}u}}$，我們得到

${\frac {\partial \phi }{\partial t}}{\frac {\partial \psi }{\partial k}}-{\frac {\partial \psi }{\partial t}}{\frac {\partial \phi }{\partial k}}=0$

一個方程，它用於確定與初始點共軛的點。因此，透過0並滿足微分方程 $G=0$ 的曲線的接觸點，必須是與0共軛的點。

但這隻有在曲線 ${\bar {x}}=f(u),{\bar {y}}=g(u)$ 與包絡線重合時才有可能；而根據我們的假設，曲線031應該完全位於包絡線所包圍的區域內。由此可見，在該區域內不可能存在這樣的曲線031，使得滿足微分方程 $G=0$ 並連線點0與031上一點的每條曲線都同時與031相切。

因此，量 $q{\bar {p}}-p{\bar {q}}$ 只有當0和1之間的任意曲線在其整個範圍內始終與透過0並滿足微分方程 $G=0$ 的曲線之一重合時，才能處處為零。但由於在我們定義的範圍內，在包圍場的表面帶內，只能畫出一條透過0和1並滿足微分方程 $G=0$ 的曲線，因此，任意曲線031只能與原始曲線01重合，然後它就不是該曲線的變分。因此，可以得出結論：函式 ${\mathcal {E}}$ 不能對所有經過變分的曲線點都為零。

第164條.
曲線031不必在其整個範圍內都是一條規則曲線的單一軌跡。如果我們假設031由任意數量的規則曲線段組成，則積分可以看作是各個曲線段上的積分之和，並且上述結論也適用。

可能會出現曲線的一部分在其整個範圍內與透過0點並滿足微分方程$G=O$的其中一條曲線的某一部分重合。如果這種情況發生在23上，例如，使得${\mathcal {E}}$沿著23為零，那麼我們可以用曲線$2'3$的任意一部分來替換這部分曲線，該曲線非常靠近23。然後，上面證明的定理對於曲線$02'31$成立，即

$I_{03}{\overset {>}{<}}I_{02'}+{\bar {I}}_{2'3}$

根據函式${\mathcal {E}}$在曲線$02'31$上是否處處非正或處處非負而定。現在，如果我們將曲線$2'3$儘可能靠近曲線23，則差$I_{03}-I_{02'}-{\bar {I}}_{2'3}$的絕對值可以小於任意小的量$\delta$；並且，根據上面證明的內容，在第一種情況下，差$I_{03}-I_{02'}-{\bar {I}}_{2'3}$肯定不負，而在第二種情況下它不正。

如果我們將點3沿著任意曲線進一步推向1，那麼當3到達4的鄰域時，再次得出$I_{04}-I_{03}-{\bar {I}}_{34}$大於或小於零，並且，如上所述，我們看到積分$I_{01}$（在滿足微分方程$G=0$的曲線上擴充套件）大於或小於在任意曲線0231上取的積分，根據函式${\mathcal {E}}$是否處處非負或處處非正而定。

第165條.
此外，為了得出我們的結論，不需要使經過變分的曲線的部分是規則的，只要座標可以表示為某個量的函式，並且這些函式具有導數即可。最後，如果我們認為所做的變分是完全任意的，以至於只給出了點的位 置，而不知道它們的座標是否具有導數，那麼確實在這條曲線上取的積分不再有任何意義。但是，積分的含義可以擴充套件，使其即使在這種情況下也具有意義。因為如果我們首先假設經過變分的曲線的座標可以透過具有導數的函式來表示，那麼在曲線上取的積分是

$\int _{t_{0}}^{t_{1}}F[f(t),g(t),f'(t),g'(t)]{\text{d}}t$

該積分被分解成多個積分的和（對應於區間 $t_{0}\ldots \tau _{1},\tau _{1}\ldots \tau _{2},\ldots ,\tau _{n}\ldots t_{1}$），等於

$\int _{t_{0}}^{\tau _{1}}F{\text{d}}t+\int _{\tau _{1}}^{\tau _{2}}F{\text{d}}t+\cdots +\int _{\tau _{n}}^{t_{1}}F{\text{d}}t$ \qquad (C)

我們假設點 $x_{0},y_{0};x_{1},y_{1};\ldots x_{n},y_{n};x_{n+1},y_{n+1}$分別對應於值 $t_{0}m\tau _{1},\ldots \tau _{n},t_{1}$。

然後我們有

$x_{1}-x_{0}=f'(t_{0})(\tau _{1}-t_{0})+(\tau _{1}-t_{0})[\tau _{1}-t_{0}]$

$..........................................$

$x_{n+1}-x_{n}=f'(\tau _{n})(t_{1}-\tau _{n})+(t_{1}-\tau _{n})[t_{1}-\tau _{n}]$

$y_{1}-y_{0}=g'(t_{0})(\tau _{1}-t_{0})+(\tau _{1}-t_{0})[\tau _{1}-t_{0}]$

$..........................................$

$y_{n+1}-y_{n}=g'(\tau _{n})(t_{1}-\tau _{n})+(t_{1}-\tau _{n})[t_{1}-\tau _{n}]$

其中$[\tau _{v}-\tau _{v-1}]$表示一個量，它與$\tau _{v}-\tau _{v-1}$同時變為無限小。

對於表示式（C）中的第一個積分，我們寫成

$x=x_{0}+x_{0}'(t-t_{0})+(t-t_{0})[t-t_{0}]$

$y=y_{0}+y_{0}'(t-t_{0})+(t-t_{0})[t-t_{0}]$

$x'=x_{0}'+x_{0}''(t-t_{0})+(t-t_{0})[t-t_{0}]$

$y'=y_{0}'+y_{0}''(t-t_{0})+(t-t_{0})[t-t_{0}]$

對於第二個積分，我們寫成

$x=x_{1}+x_{1}'(t-\tau _{1})+(t-\tau _{1})[t-\tau _{1}]$

$y=y_{1}+y_{1}'(t-\tau _{1})+(t-\tau _{1})[t-\tau _{1}]$

其他積分也類似。

我們將這些表示式寫到積分和（C）中，並展開成冪級數，透過積分得到

$(\tau _{1}-t_{0})F(x_{0},y_{0},x_{0}',y_{0}')+(\tau _{2}-\tau _{1})F(x_{1},y_{1},x_{1}',y_{1}')+\cdots +(t_{1}-\tau _{n})F(x_{n},y_{n},x_{n}',y_{n}')\ldots$

加上相同數量的項，這些項相對於量$\tau _{v}-\tau _{v-1}$而言，變為無限小的二階量。

因此，我們可以將積分寫成以下形式

$\lim _{n\rightarrow \infty }\left(\sum _{v=1}^{n+1}F(x_{v-1},y_{v-1},x_{v-1}',y_{v-1}')\right)$

其中，我們必須理解$\tau _{0}$ 表示值為 $t_{0}$，而 $t_{n+1}$ 表示值為 $t_{1}$。

由於 $\tau _{v}-\tau _{v-1}$ 是正數，並且函式 $F$ 關於 $x_{1}',y_{1}'\ldots$ 是齊次的一階函式，我們可以將上述極限寫成如下形式：

$\lim _{n\rightarrow \infty }\left(\sum _{v=1}^{n+1}F(x_{v-1},y_{v-1},(\tau _{v}-\tau _{v-1})x_{v-1}',(\tau _{v}-\tau _{v-1})y_{v-1}')\right)$

或者，由於

$x_{v}-x_{v-1}=(\tau _{v}-\tau _{v-1})x_{v-1}'+(\tau _{v}-\tau _{v-1})[\tau _{v}-\tau _{v-1}]$

上述表示式為

$\lim _{n\rightarrow \infty }{\big (}F(x_{0},y_{0},x_{1}-x_{0},y_{1}-y_{0})+\cdots +F(x_{n},y_{n},x_{n+1}-x_{n},y_{n+1}-y_{n}){\big )}$

第 166 條

.
上述形式的積分比迄今為止使用的積分具有更一般的意義，但它在後者有意義的任何特定情況下都與後者重合。關於任意變分，我們可以假設一系列點$x_{0},y_{0};x_{1},y_{1};\ldots x_{n},y_{n};x_{n+1},y_{n+1}$，其性質是任意兩個相鄰點之間的距離不超過某個量$\delta$。

然後我們形成和

$F(x_{0},y_{0},x_{1}-x_{0},y_{1}-y_{0})+\cdots +F(x_{n},y_{n},x_{n+1}-x_{n},y_{n+1}-y_{n})$

如果我們使$\delta$越來越小，透過增加點的數量，可能會發生這種情況，即這個和接近一個確定的極限。我們稱此極限為沿曲線取的積分的值。也可能發生極限不接近一個確定的值；例如，它可能在兩個值之間擺動。然後我們說沿此曲線取的積分沒有意義。

如果我們想到在曲線上取的一系列點，依次用折線連線起來，那麼沿著這條折線取的積分將接近與沿著曲線取的積分相同的極限，如果積分有意義。

因此，如果給定一條曲線01，它滿足迄今為止為最大值或最小值所做的所有條件，並且如果這條曲線以任意方式變化，那麼如果沿著已進行變分的曲線的積分如上所定義具有意義，那麼我們可能會畫一條折線，沿著它取的積分與沿著已導致變化的曲線的積分的偏差可以任意小，並且第161條的定理適用於該曲線。因此，我們可以說， *在最大值的情況下，沿著已進行變分的曲線的積分不能大於沿著原始曲線的積分，而在最小值的情況下，它不能小於沿著原始曲線的積分。*

由於我們可以在所有變分都存在的區域內使其儘可能窄，因此我們可以假設在已進行變分的曲線上存在一個點3，它非常靠近01（但不在其上），使得可以在點0和3之間以及3和1之間畫出兩條曲線03、31，它們也滿足問題的全部條件。

為了簡潔起見，讓我們假設我們必須處理最大值。那麼，正如我們剛才看到的，沿著03和31的積分絕不小於沿著已進行變分的曲線的相應部分的積分；但是，根據前面的定理，沿著01取的積分大於沿著03和31取的積分之和，因此也大於沿著已進行變分的曲線的積分。因此，實際上存在最大值。

第167條.
我們現在可以研究函式${\mathcal {E}}$在最後在第140-144條中考慮的四個問題的情況下的行為。

旋轉曲面面積最小的曲線問題。

我們看到，在沒有一對共軛點存在的範圍內，懸鏈線是當繞半平面軸旋轉時描述最小面積曲面的曲線。從點$P_{0}$開始，我們可以朝任何方向畫一條滿足微分方程$G=0$（懸鏈線）的曲線；函式$F_{1}$對於這些曲線中的每一條都是正的，只要我們將自己限制在$y$為正的半平面中。因此，實際上將進入一個真正的最小值。因為如果$p,q$是懸鏈線上任意一點的切線的方向餘弦，${\bar {p}},{\bar {q}}$是透過同一點的任意曲線的切線的方向餘弦，那麼，由於關係

$F^{(1)}(x,y,x',y')={\frac {yx'}{\sqrt {x'^{2}+y'^{2}}}}\qquad F^{(2)}(x,y,x',y')={\frac {yy'}{\sqrt {x'^{2}+y'^{2}}}}$

由此可得

$F^{(1)}(x,y,x',y')=yp\qquad F^{(2)}(x,y,x',y')=yq$

因為

$p^{2}+q^{2}=1$

因此

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=y{\big (}({\bar {p}}-p){\bar {p}}+{\bar {q}}-q){\bar {q}}{\big )}=y{\big (}1-(p{\bar {p}}+q{\bar {q}}){\big )}$

表示式$p{\bar {p}}+q{\bar {q}}$ 是兩條切線之間夾角的餘弦。因此，我們看到函式${\mathcal {E}}$對於我們考慮的任何點都不是負數，並且對於任何兩個方向$p,q$ 和 ${\bar {p}},{\bar {q}}$ 都是如此。

因此，如果曲線上的任何一點都沒有$y=0$，則我們之前的結論適用，並且積分的最小值實際上已經找到。

第 168 條.
最速降線。我們看到這條曲線是擺線

$x=g+r(1-\sin t)\qquad y+a=r(1-\cos t)$

我們假設運動點開始的點$A$是座標原點，並且該點具有與量${\sqrt {a}}$成正比的初速度；$Y$軸是重力方向。我們已經看到，擺線可以透過一個在直線$y=-a$上滾動的圓上的一個點來生成。如果$a$不等於零，則可以透過$A$在任意方向上構造擺線的一段弧。如果曲線透過一個奇異點，那麼它不會使積分最小化，如第 104 節所示。如果$A$和$B$不是奇異點，則函式$F_{1}$在這條曲線上以及其周圍各個方向上的鄰域內都具有一個不為零的正值。

在任意兩個點之間（參見第 105 節），當量$a$給出時，總是可以且只能畫出一段擺線弧，在這兩個點之間沒有奇異點。因此，如果$a$不等於零，並且因此$A$和$B$不是奇異點，那麼（參見第 159 節）由此可知，該曲線實際上使積分具有最小值。假設$A$或$B$是奇異點；那麼在這一點上$F_{1}$變為無窮大，這種情況將在下一節中討論。

第 169 節

.
假設$A$ 是一個奇點，且$a=0$。在$A$ 和 $B$ 之間畫一條任意曲線。在這條曲線上，在$A$ 附近取一點$A_{1}$，並過$A_{1}$ 和 $B$ 作一條擺線，該擺線與$X$軸交於$A_{1}'$。質點在重力作用下透過$A_{1}$時的速度，與它如果沿著過$A$ 和 $B$ 作出的擺線上，在$X$軸下方相同距離處具有的速度相同。

可以引入以下符號：

用$I_{01}$ 表示質點沿擺線$A_{1}'B$ 從$A_{1}'$ 跌落到$B$ 的時間。

用$I_{01}'$表示在任意曲線$AB$上，從$A$到$A_{1}$下落的 時間。

用$I$表示在擺線$A_{1}B$上，從$A_{1}$到$B$下落的 時間。

用$I'$表示在任意曲線$A_{1}B$上，從$A_{1}$到$B$下落的 時間。

我們已經證明了

$I'>I$

因此，如果我們寫

${\bar {I}}=I_{01}'+I'$

由此可得

${\bar {I}}>I+I_{01}'$

現在，讓點$A_{1}$越來越靠近點$A$，使得積分$I$接近極限$I_{01}$，而$I_{01}'$變得無限小。那麼我們必須有

${\bar {I}}\geq I_{01}$

可以看出，${\bar {I}}$大於$I_{01}$，如下所示：只要曲線的一部分上$G\neq 0$，我們就可以以這樣的方式改變它，使得相應積分的增量可以具有任何符號。因此，如果整個曲線$AA_{1}B$上$G\neq 0$，我們可以用另一條曲線代替它，如果$I''$是屬於它的積分的值，

$I''<{\bar {I}}$

但是，我們也有

$I''\geq I_{01}$

由此可得

${\bar {I}}>I_{01}$

另一方面，如果整個曲線$AA_{1}B$上$G=0$，則這條曲線必須由幾個擺線弧組成；因為，如果它只有一條，曲線$AA_{1}B$和$AB$將是相同的。這些弧在它們連線處的切線必須不同；因為，由於該點不可能位於$X$軸上，具有相同方向的連續點必須位於相同的擺線弧上。但是，如果存在角，則可以將它們圓滑，以便這兩點之間存在更短的路徑，因此，如果速度相同，則下落時間將更短。

因此，在$A$和$B$之間，擺線弧也使下落時間最短，在這種情況下$A$是一個奇點；也就是說，當質點從$A$開始，初始速度為零。

先前得出的結論，如果$B$ 是一個奇點，也同樣適用；因為物質點是從$B$ 上升到$A$ 還是從$A$ 下降到$B$ 並沒有什麼區別，如果我們允許物質點以到達$B$時相同的初速度返回。在返回途中，它將以其原始速度到達$A$。在這兩種情況下，它在曲線上所有點的速度都相同，但方向相反。兩種情況下曲線上的積分值相同；因此，使積分取最小值的曲線在第二種情況下也將使積分最小。

第 170 條.
球面上測地線的求解問題在此沒有特別的興趣。可以發現函式${\mathcal {E}}$ 在位於兩個極點之間的大圓弧上保持正號。

第 171 條.
阻力最小的旋轉曲面問題。

在這個問題中

$F()x,y,x',y')={\frac {xx'^{3}}{x'^{2}+y'^{2}}}$

並且由於

$p^{2}+q^{2}=1$

由此可得

$F(x,y,p,q)={\frac {xp^{3}}{p^{2}+q^{2}}}=xp^{3}$

${\frac {\partial F}{\partial p}}=x(p^{4}+3p^{2}q^{2})\qquad {\frac {\partial F}{\partial q}}=-2xp^{3}q$

將這些值代入

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=F(x,y,{\bar {p}},{\bar {q}})-{\bar {p}}{\frac {\partial F}{\partial p}}-{\bar {q}}{\frac {\partial F}{\partial q}}$

我們有

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=x[{\bar {p}}^{3}-{\bar {p}}p^{2}-2{\bar {p}}p^{2}q^{2}+2{\bar {q}}p^{3}q]$

$\qquad =x[{\bar {p}}({\bar {p}}^{2}-p^{2})+2p^{2}q(p{\bar {q}}-{\bar {p}}q)]$

$\qquad =x[{\bar {p}}({\bar {p}}^{2}(p^{2}+q^{2})+2p^{2}q(p{\bar {q}}-{\bar {p}}q))+2p^{2}q(p{\bar {q}}-{\bar {p}}q)]$

$\qquad =x({\bar {p}}q-p{\bar {q}})[{\bar {p}}({\bar {p}}q+p{\bar {q}})-2p^{2}q]$

$\qquad =x({\bar {p}}q-p{\bar {q}})[{\bar {q}}({\bar {q}}q-p{\bar {q}})(p^{2}+q^{2})+2p{\bar {p}}{\bar {q}}(p^{2}+q^{2})-2p^{2}q({\bar {p}}^{2}+{\bar {q}}^{2})]$

$\qquad =x({\bar {p}}q-p{\bar {q}})[{\bar {p}}({\bar {p}}q-p{\bar {q}})(p^{2}+q^{2})-2p^{2}{\bar {p}}({\bar {p}}q-p{\bar {q}})+2pq{\bar {q}}({\bar {p}}q-p{\bar {q}})]$

$\qquad =x({\bar {p}}q-p{\bar {q}})[{\bar {p}}(p^{2}+q^{2})-2p^{2}{\bar {p}}+2pq{\bar {q}}]$

$\qquad =x({\bar {p}}q-p{\bar {q}})[{\bar {p}}(q^{2}-p^{2})+2pq{\bar {q}}]$

寫作

$\cos {\bar {\tau }}={\bar {p}}\qquad \sin {\bar {\tau }}={\bar {q}}\qquad \cos \tau =p\qquad \sin \tau =q$

我們有

${\mathcal {E}}(x,y,p,q,{\bar {p}},{\bar {q}})=-x\sin({\bar {\tau }}-\tau )^{2}\cos({\bar {\tau }}+2\tau )$

因此，${\mathcal {E}}$ 的符號與 $-\cos({\bar {\tau }}+2\tau )$ 的符號相同，並且可以透過適當選擇 ${\bar {\tau }}$（一個取決於 ${\bar {p}},{\bar {q}}$ 的角度）使其為正或負。

在曲線的每個 $x\neq 0$ 的點上，函式 ${\mathcal {E}}$ 可以具有不同的符號，因此積分的最大值或最小值不存在。我們在第 109 節中看到，對於弧的所有點，$x$ 必須不等於零。

第 172 節.
勒讓德 *（關於在變分法中區分最大值和最小值的方法的回憶錄）* 指出，透過採用鋸齒線作為生成曲線，阻力可以任意小。

假設弧 $P_{1}P_{2}$ 具有生成最小阻力表面的所需特性，並且假設該曲線的切線在任何地方都不平行於 $X$ 軸。寫成 $p={\frac {{\text{d}}x}{{\text{d}}y}}$，則可知沿弧 $P_{1}P_{2}$，$p\neq 0$。

然後我們有（第 108 節）

$I_{1,2}=\int _{t_{1}}^{t_{2}}{\frac {xx'^{3}}{x'^{2}+y'^{2}}}{\text{d}}t=\int _{x_{1}}^{x_{2}}{\frac {p^{2}x}{1+p^{2}}}{\text{d}}x$

由於 $p$ 在所討論的弧線上是有限且連續的，因此 ${\frac {p^{2}}{1+p^{2}}}$ 在該弧線上具有相同的特性，因此

$I_{1,2}={\frac {p_{0}^{2}x}{1+p_{0}^{2}}}\int _{x_{1}}^{x_{2}}x~{\text{d}}x={\frac {p_{0}^{2}x}{1+p_{0}^{2}}}{\frac {x_{2}^{2}-x_{1}^{2}}{2}}$

其中，$p_{0}$ 是 $p$ 的平均值，位於曲線上的點 $P_{1}$ 和 $P_{2}$ 之間。

在$P_{1}$和$P_{2}$的縱座標之間作一條平行於$Y$軸的直線，並在該直線上取一點$P_{3}$，其縱座標大於點$P_{1}$和$P_{2}$的縱座標。作直線$P_{1}P_{3}$和$P_{2}P_{3}$，並設$p_{1}$和$p_{2}$分別為這些直線的${\frac {{\text{d}}x}{{\text{d}}y}}$的值。沿折線$P_{1}P_{3}P_{2}$的積分$\int F{\text{d}}t$可以表示為$I_{13}+I_{32}$，其中

$I_{13}=\int _{x_{1}}^{x_{3}}{\frac {p_{1}^{2}x}{1+p_{1}^{2}}}{\text{d}}x={\frac {p_{1}^{2}}{1+p_{1}^{2}}}{\frac {x_{3}^{2}-x_{1}^{2}}{2}}$

以及

$I_{32}=\int _{x_{3}}^{x_{2}}{\frac {p_{2}^{2}x}{1+p_{2}^{2}}}{\text{d}}x={\frac {p_{2}^{2}}{1+p_{2}^{2}}}{\frac {x_{2}^{2}-x_{3}^{2}}{2}}$

然後我們有

$I_{132}-I_{12}=I_{13}+I_{32}-I_{12}={\frac {p_{1}^{2}(x_{3}^{2}-x_{1}^{2})}{2(1+p_{1}^{2})}}+{\frac {p_{2}^{2}(x_{2}^{2}-x_{3}^{2})}{2(1+p_{2}^{2})}}-{\frac {p_{0}^{2}(x_{2}^{2}-x_{1}^{2})}{2(1+p_{0}^{2})}}$

該表示式的前面兩項可以透過充分減小量$p_{1}$ 和 $p_{2}$ 來任意地減小，這可以透過沿著其縱座標無限地移除點$P_{3}$ 來實現。因此，它們的和小於第三項，因此，

$I_{132}<I_{12}$

此結果也可以如下推導：

${\frac {I_{13}+I_{32}}{I_{12}}}={\frac {p_{1}^{2}(1+p_{0}^{2})}{p_{0}^{2}(1+p_{1}^{2})}}{\frac {x_{3}^{2}-x_{1}^{2}}{x_{2}^{2}-x_{1}^{2}}}+{\frac {p_{2}^{2}(1+p_{0}^{2})}{p_{0}^{2}(1+p_{2}^{2})}}{\frac {x_{2}^{2}-x_{3}^{2}}{x_{2}^{2}-x_{1}^{2}}}<{\frac {p_{1}^{2}(1+p_{0}^{2})}{p_{0}^{2}(1+p_{1}^{2})}}+{\frac {p_{2}^{2}(1+p_{0}^{2})}{p_{0}^{2}(1+p_{2}^{2})}}$

因為 $x_{1}<x_{3}<x_{2}$。

因此，更進一步地

${\frac {I_{13}+I_{32}}{I_{12}}}=<(p_{1}^{2}+p_{2}^{2}){\frac {1+p_{0}^{2}}{p_{0}^{2}}}$

由此可見，比率 ${\frac {I_{13}+I_{32}}{I_{12}}}$ 可以透過適當選擇 $p_{1}$ 和 $p_{2}$ 而無限減小。因此，阻力的最小值沒有限制。

上述方法並沒有取代 ${\mathcal {E}}$判據，該判據表明不存在最小阻力表面。它僅僅表明不存在旋轉面，該旋轉面給出阻力的絕對最小值——小於任何其他鄰近表面的阻力。 ${\mathcal {E}}$判據表明，在有限鄰域內，不存在給出小於任何鄰近曲線給出的阻力的最小值。

第173條

.
一般情況下，當$F(x,y,x',y')$ 是 $x'$ 和 $y'$ 的有理函式時，則不存在最大值或最小值。因為在這種情況下

${\mathcal {E}}=F(x,y,{\bar {p}},{\bar {q}})-{\bar {p}}{\frac {\partial F}{\partial p}}-{\bar {q}}{\frac {\partial F}{\partial q}}$

也是 ${\bar {p}}$ 和 ${\bar {q}}$ 的有理函式，並且對於這些量是一次齊次的。因此

${\mathcal {E}}(x,y,k{\bar {p}},k{\bar {q}})=k{\mathcal {E}}(x,y,{\bar {x}},{\bar {y}})$

因此

${\mathcal {E}}(x,y,-{\bar {p}},-{\bar {q}})=-{\mathcal {E}}(x,y,{\bar {p}},{\bar {q}})$

因此可以看出，我們只需要反轉位移的方向，就可以使函式 ${\mathcal {E}}$ 的符號發生變化。

第 174 條.
我們現在已經完全解決了第一章提出的四個問題，同時也完成了變分法的核心部分之一。在簡要陳述已經確立的四個判據之後，我們將開始第二部分，其目的是對問題的理論和實踐解決方案進行探討，這類問題的典型代表是第一章中的問題 V 和 VI。

這些判據可以概括如下（參見第 125 條）：積分

$I=\int _{t_{0}}^{t_{1}}F(x,y,x',y'){\text{d}}t$

其中$F$是其四個自變數的單值正則函式，並且關於$x'$和$y'$是一次齊次函式，如果

1) *曲線上的每一點都滿足微分方程$G=0$；*

2) $F_{1}$*在整個區間$t_{0}\ldots t_{1}$內始終為正或始終為負；*

3) *在區間$t_{0}\ldots t_{1}$（包括端點）內不存在曲線的共軛點；*

4) *函式${\mathcal {E}}$在整個區間$t_{0}\ldots t_{1}$內始終為正或始終為負；*

在本討論中，我們排除了以下情況：

1) *曲線的端點是共軛點；*

2) $F_{1}=0$*對於曲線上的某一點成立；*

3) $F_{1}=0$*對於曲線上的某一段成立；*

4) ${\mathcal {E}}=0$*對於曲線上的某一點或某一段成立。

對前三種情況進行一般性處理需要將理論擴充套件到更高階的變分。否則，在遇到上述任何一種特殊情況時，必須在每個例子中採用特定的方法。

第175條.
在我們開始考慮*相對極大值和極小值*之前，我們至少可以指出該理論的自然擴充套件和推廣：與其確定*第一類結構**在兩個量域中的情況，不如要求確定*第一類結構*在$n$個量域中的情況。*

如果在$n$個量$x_{1},x_{2},\ldots ,x_{2}$的域中確定了一個第一類結構，則其中$n-1$個量可以表示為剩餘一個量的函式，例如，$x_{1}$。

寫作

$u=\int F\left(x_{1},x_{2},\ldots ,x_{n},{\frac {{\text{d}}x_{2}}{{\text{d}}x_{1}}},{\frac {{\text{d}}x_{3}}{{\text{d}}x_{1}}},\ldots ,{\frac {{\text{d}}x_{n}}{{\text{d}}x_{1}}}\right){\text{d}}x_{1}$

可以看出，$u$ 與 $n-1$ 個函式相關聯，

${\frac {{\text{d}}u}{{\text{d}}x_{1}}}=F\left(x_{1},x_{2},\ldots ,x_{n},{\frac {{\text{d}}x_{2}}{{\text{d}}x_{1}}},{\frac {{\text{d}}x_{3}}{{\text{d}}x_{1}}},\ldots ,{\frac {{\text{d}}x_{n}}{{\text{d}}x_{1}}}\right)$

$u$ 在結構初始點和終點的值的差由一個定積分表示。

當我們將 $x$ 表示為 $t$ 的函式，例如 $x_{1}=x_{1}(t),x_{2}=x_{2}(t),\ldots ,x_{n}=x_{n}(t)$時，該積分的形式為：

$I=\int _{t_{0}}^{t_{1}}F(x_{1},x_{2},\ldots ,x_{n},x_{1}',x_{2}',\ldots ,x_{n}'){\text{d}}t$

函式 $F$ 必須在其自變數的整個固定域或固定域的一部分內是一個單值、正則函式。

積分$I$的值與變數$x_{1},x_{2},\ldots ,x_{n}$如何表示為$t$的函式無關。因此，根據第68條的類似內容，函式$F$受到進一步的限制：

$kF(x_{1},x_{2},\ldots ,x_{n},x_{1}',x_{2}',\ldots ,x_{n}')=F(x_{1},x_{2},\ldots ,x_{n},kx_{1}',kx_{2}',\ldots ,kx_{n}')$

其中$k$是一個正常數。

因此，第13條中給出的問題的推廣可以表述如下：

需要確定$n$個量$x_{1},x_{2},\ldots ,x_{n}$作為量$t$的函式，使得透過以下方程定義的分析結構

$x_{1}-x_{1}(t),x_{2}=x_{2}(t),\ldots ,x_{n}=x_{n}(t)$

積分的值

$I=\int _{t_{0}}^{t_{1}}F(x_{1},x_{2},\ldots ,x_{n},x_{1}',x_{2}',\ldots ,x_{n}'){\text{d}}t$

達到最大值或最小值；換句話說，如果使上述分析結構發生無限小的變化，則由此產生的積分的變化在最大值的情況下必須始終為負，在最小值的情況下必須始終為正。此外，函式$F$應被視為其自變數的單值正則函式，並且關於$x_{1}',x_{2}',\ldots ,x_{n}'$而言，是一個一階齊次函式。

第176條.
發現上述問題的處理與第13條中給出的問題完全類似。當變數$x_{1},x_{2},\ldots ,x_{n}$之間存在條件方程時，會產生更大的複雜性。我們在第一章的第三題中遇到過這種型別的例子。

這個問題可以這樣表述：在屬於曲面

$f(x,y,z)=0$

的所有空間曲線中，確定一條使積分

$\int _{t_{0}}^{t_{1}}{\sqrt {x'^{2}+y'^{2}+z'^{2}}}{\text{d}}t$

是最小值。

一般問題可以表述如下：在量$x_{1},x_{2},\ldots ,x_{n}$的定義域中的一類結構中，對於其$m$個方程

$f_{\mu }(x_{1},x_{2},\ldots ,x_{n})=0\qquad \mu =1,2,\ldots ,m;~~m<n-1$

存在，需要確定的是使得積分

$I=\int _{t_{0}}^{t_{1}}F(x_{1},x_{2},\ldots ,x_{n},x_{1}',x_{2}',\ldots ,x_{n}'){\text{d}}t$

達到最大值或最小值的那個結構。

這個問題可以透過類似於第10條中關於曲面上最短線的處理方法，簡化為上一條中的問題。這$m$個條件方程可以透過將變數$x_{1},x_{2},\ldots ,x_{n}$表示為$n-m$個新變數的函式來滿足，方法是在《最大值與最小值理論講義》等，第一章第15條中給出的。這些新變數彼此獨立，因此上述積分可以用一個變數不受外部條件約束的積分來代替；或者我們可以像在最大值與最小值理論中處理變數受輔助條件約束的情況一樣進行處理（同上，第54頁）。

第177條.
變分法的更一般的問題，就其與一類結構相關的部分而言，可以表述如下

在$n$個量$x_{1},x_{2},\ldots ,x_{n}$的定義域中的一類結構中，不僅在這些$n$個量本身之間，而且還在其一階導數之間存在確定條件方程的情況下，需要確定的是使得積分

$I=\int _{t_{0}}^{t_{1}}F(x_{1},x_{2},\ldots ,x_{n},x_{1}',x_{2}',\ldots ,x_{n}'){\text{d}}t$

達到最大值或最小值的那個結構。

很容易證明，$F$是$x_{1},x_{2},\ldots ,x_{n}$以及這些量的二階及更高階導數的函式的看似更一般的情況包含在剛才陳述的問題中。為了簡單起見，我們考慮只有兩個變數的情況，並寫成

$u=\int _{x_{1}}^{x_{2}}F\left(x,y,{\frac {{\text{d}}y}{{\text{d}}x}},{\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}},\ldots \right){\text{d}}x$

如果在這個積分中我們將$x$和$y$表示為$t$的函式，則有

${\frac {{\text{d}}y}{{\text{d}}t}}={\frac {{\text{d}}y}{{\text{d}}x}}x'\qquad {\frac {{\text{d}}^{2}y}{{\text{d}}t^{2}}}={\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}x'^{2}+{\frac {{\text{d}}y}{{\text{d}}x}}x''$

因此，我們可以將積分$u$改為

$u=\int _{t_{0}}^{t_{1}}F(x,y,x',y',x'',y'',\ldots ){\text{d}}t$

我們還有

${\frac {{\text{d}}x'}{{\text{d}}t}}-x''=0\qquad {\frac {{\text{d}}y'}{{\text{d}}t}}-y''=0$

因此，我們可以寫成

$u=\int _{t_{0}}^{t_{1}}F\left(x,y,x_{1},y_{1},{\frac {{\text{d}}x_{1}}{{\text{d}}t}},{\frac {{\text{d}}y_{1}}{{\text{d}}t}}\right){\text{d}}t$

以及條件方程

${\frac {{\text{d}}x}{{\text{d}}t}}=x_{1}\qquad {\frac {{\text{d}}y}{{\text{d}}t}}=y_{1}$

如果在$F$中只出現一階和二階導數，則可以看出$F$取決於需要確定的四個函式$x,y,x_{1},y_{1}$，同時必須滿足剛才寫出的兩個條件方程。屬於剛剛陳述的廣義問題的一類問題是第17節中提出的問題，將在後續章節中進行討論。

第178節.
最後可以提到，如果我們要求確定更高型別的結構，則變分法的這個問題可以進一步推廣。例如，在最簡單的情況下，三個量$x,y,z$可以被確定為兩個獨立變數$u$和$v$的函式。然後，我們不是隻有一個積分，而是有二重積分

$\int \int F\left(x,y,z,{\frac {\partial x}{\partial u}},{\frac {\partial y}{\partial u}},{\frac {\partial z}{\partial u}},{\frac {\partial x}{\partial v}},{\frac {\partial y}{\partial v}},{\frac {\partial z}{\partial v}}\right){\text{d}}u{\text{d}}v$

它必須是最大值或最小值。

對這個問題的研究將給出極小曲面理論。