電路理論/聯立方程/示例 1

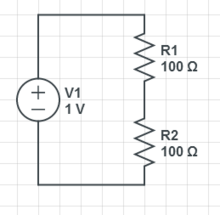
原始示例 1 電路

求解所有未知電壓和電流。

標註

示例 1 電路，標註了電壓和電流，1 個迴路，無節點

目標是標記未知量和已知量。原始問題已建立符號 $V1,R1{\text{ and }}R2$ 並賦予它們值。它們似乎是已知量。此時標記的未知量為 $i_{1},v_{R1}{\text{ and }}v_{R2}$.

此處顯示相關源方程。

迴路

該電路中有一個迴路。它以順時針方向繪製，在直線上新增一個箭頭，並在迴路上新增符號 $L_{1}$。此符號將是來自此箭頭的迴路方程的名稱。

接下來，在電阻器上新增與電壓相關的 + 和 -，以指示電路中的極性關係（從繪製的迴路開始）。

重要的是要記住，在這一點上，+ 和 - 以及迴路都包含電路拓撲資訊。它們不是對最終數值答案的“猜測”。

節點

該電路中沒有節點。有三個微不足道的節點，但所有三個節點的電流都相同。此時選擇電流方向。

此時選擇電流方向。現在，在圖紙上新增箭頭以指示方向。它不是任意的。電流必須流入元件的 + 端並流出 - 端。

電壓電源的 + 端的電流是流出還是流入並不重要，因為電壓電源會根據電路的其餘部分改變其電流。

方程計數

第一步是列出變數以及它們是已知量還是未知量。
$V_{1}=1volt$
$R_{1}=100ohm$
$R_{2}=100ohm$
$i_{1}=?amp$
$v_{R1}=?volt$
$v_{R2}=?volt$

因此，有三個未知量，需要三個方程。

端點方程

有兩個器件可以寫出端點方程
$TR1:v_{R1}=i_{1}*R_{1}$
$TR2:v_{R2}=i_{1}*R_{2}$

電源沒有端點方程。

迴路方程

只有一個迴路方程
$L1:v_{R1}+v_{R2}-V_{1}=0$

電源電壓為負，因為迴路方向進入電源負極。

節點方程

沒有節點，因此沒有節點方程。如果要統計三個平凡節點，將會有三個電流：分別流過每個元件（兩個電阻和電源）。這時需要寫下三個平凡方程，說明它們彼此相等（取決於方向）。下一個例子將探索節點。

求解方程

三個方程為
${\begin{cases}TR1:{\text{ }}v_{R1}=i_{1}*R_{1}\\TR2:{\text{ }}v_{R2}=i_{1}*R_{2}\\L1:{\text{ }}v_{R1}+v_{R2}-V_{1}=0\end{cases}}$

代數

求解方案概述

• 將 TR:1 和 TR:2 代入 L1:，求解未知量 $i_{1}$
• 將電流解代入 TR:1 和 TR:2，求解未知量 $v_{R1}v_{R2}$
• 將已知值代入符號以獲得數值解

代數符號解

• $i_{1}={\frac {V_{1}}{R_{1}+R_{2}}}$
• $v_{R1}={\frac {V_{1}*R_{1}}{R_{1}+R_{2}}}$
• $v_{R2}={\frac {V_{1}*R_{2}}{R_{1}+R_{2}}}$

代數數值解

• $i_{1}={\frac {1}{100+100}}={\frac {1}{200}}=0.005amp$
• $v_{R1}={\frac {1*100}{100+100}}={\frac {100}{200}}={\frac {1}{2}}=0.5volt$
• $v_{R2}={\frac {1*100}{100+100}}={\frac {100}{200}}={\frac {1}{2}}=0.5volt$

這是一個簡單的例子。但我們的目標是練習所有數學工具。將來這些工具中的一種或多種可能會失效。我們的目標是現在體驗使用這些工具的成功，這樣我們就知道失敗是什麼樣子的。

微分方程

在本例中沒有微分方程，但本課程有四分之三時間在討論這種複雜的電路，使用電容和電感代替電阻，並檢視微分方程。

符號計算

Wolfram Alpha

File:Ex1wolf.png

Mathematica 對示例 1 的解決方案

點選上面的連結，進入 Wolfram 網站，檢視輸入的語法和答案。注意以下幾點

• Wolfram Alpha 處理不了“i”，它可能認為它是一個虛數。所以需要切換到“k”。
• Wolfram Alpha 處理不了雙下標，所以需要從 R1 切換到 2，從 R2 切換到 3。

一個不能解釋我們符號的自然語言符號直譯器有什麼意義？如果我們必須將我們的符號對映到它理解的符號，為什麼不直接使用 MatLab 矩陣（線性代數）呢？

Mathematica

Mathematica 與 Wolfram Alpha 有關（Alpha 表示非常早期的、粗略的草稿）。它可以工作。但看看解決方案

• 必須學習另一種標記語言
• 仍然存在下標問題

真正的問題是，用最少的按鍵、最少的錯誤、最少的符號組織或對映可以做些什麼？

Mathematica 應該得到認可，因為它嘗試了這種型別的符號解釋和計算。其他軟體包，如已停產的“TI Derive”，不支援任何下標。但 MathWorks 的符號（MuPAD）和數值（MatLab）目前提供了最佳的組合。Wolfram Alpha 為學生開始符號計算降低了門檻。這裡的目標是找出它在哪裡失效。本文將重點介紹 MathWorks 產品。

MuPad

File:Ex1matlab3.png

MathWorks MuPAD 解決方案 .. 點選 這裡 獲取可以剪下和貼上的文字 .. MuPAD 解決方案包含變數解決方案、符號解決方案和數值解決方案

MatLab 具有一個新增符號支援的符號包。啟動 MatLab，然後輸入“MuPad”。上面的方程可以輸入到 MuPAD 中，然後可以使用變數符號、精確常數和數值近似值（小數位數）來求解方程。

數值解

File:Ex1matlab4.png

Matlab 矩陣輸入，用於求解三個方程三個未知數的線性代數問題 .. 點選 這裡 剪下貼上

File:Ex1mathematica2.png

Mathematica 矩陣輸入和求解三個方程三個未知數的線性代數問題。點選 這裡 剪下貼上。

設定解決方案的步驟

• 將已知值代入方程

${\begin{cases}TR1:{\text{ }}v_{R1}=100*i_{1}\\TR2:{\text{ }}v_{R2}=100*i_{1}\\L1:{\text{ }}v_{R1}+v_{R2}-1=0\end{cases}}$

• 將方程整理，使未知數在列中，數字在等號的右側

${\begin{cases}TR1:{\text{ }}v_{R1}+0-100*i_{1}=0\\TR2:{\text{ }}0+v_{R2}-100*i_{1}=0\\L1:{\text{ }}v_{R1}+v_{R2}+0=1\end{cases}}$

• 建立兩個矩陣，一個是方陣，另一個是列向量，其中包含等號右側的數字

${\begin{array}{|c|c|c||c|}v_{R1}&v_{R2}&i_{1}&=\\\hline 1&0&-100&0\\0&1&-100&0\\1&1&0&1\\\end{array}}$

$\Rightarrow$

${\begin{bmatrix}1&0&-100\\0&1&-100\\1&1&0\end{bmatrix}}$

$\bullet$

${\begin{bmatrix}V_{R1}\\V_{R2}\\i_{1}\end{bmatrix}}$

=

${\begin{bmatrix}0\\0\\1\end{bmatrix}}$

• 將矩陣輸入到MatLab或類似的程式中

${\begin{bmatrix}V_{R1}\\V_{R2}\\i_{1}\end{bmatrix}}$

=

${\begin{bmatrix}0.5\\0.5\\0.005\end{bmatrix}}$

模擬

目標是在www.circuitlab.com中模擬。點選此連結，然後點選底部的模擬按鈕。將筆移到電路周圍。

電阻：電流為5ma，正如預測的那樣。注意電流的符號。它在-和+ 5 ma之間變化。當電流進入電阻的頂部（A）時，看起來是正的，因為電壓是正的。這使得電流為正。

電壓相對於地。電源頂部的電壓和電阻頂部的電壓相同，因為它們是同一平凡結的一部分。電壓為1伏，因為它是兩個電阻之間的電壓。底部電阻上的電壓是預測的一半。

電源：電源的相反情況也是如此。電流從電源的頂部（A）流出，標記為負。從任何東西的+端流出的電流都是負的。

功率計算

電壓和電流是恆定的。

• $P=i*v$
• $P_{source}+P_{R1}+P_{R2}=0$
• $(-.005)*1+(.005)*.5+(.005)*.5=0$

建立直覺

這是一個簡單的電路，展示了物理學中涵蓋的概念。

• 串聯的等值電阻將它們之間的電壓分配。
• 串聯的電阻分配電壓。
• 串聯電阻相加。