電路理論/聯立方程/示例 5

示例 5 電路

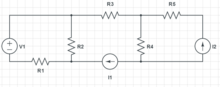
求解電流和電壓。假設電源和電阻值已知。用符號解。

從實際角度來看，在一個電路中放置多個電源是不好的做法。幾乎所有人都試圖設計只使用一個電源的電路。

從建模的角度來看，電晶體在一級近似中是一種電源。因此，在一個電路中放置多個電源是一種實踐或為更復雜的電路做準備。

標記

符號已新增

有一個電壓源，串聯一個電阻，以獲取其電流：$i_{R1}$。兩個電流源沒有與它們並聯的明確電阻，因此必須標記每個電流源的電壓：$i_{I1}$ 和 $i_{I2}$。

迴路

迴路和 + - 已新增

有三個迴路。請記住，現在的 + 和 - 不是在猜測答案的極性，而是在捕捉電路的佈局。

沒有無意義迴路（並聯元件）。

節點

恆定 EMF 部分突出顯示

節點已選擇，電流方向已在圖紙上標出

有兩個無意義節點，串聯元件共享相同的電流。一個是電壓源和 $R_{1}$ 之間。另一個是電流源 $I_{2}$ 和 $R_{5}$ 之間。

有四個非無意義節點，請檢視以不同顏色陰影顯示的恆定 EMF 區域。

這意味著可以使用三個節點。選擇哪三個並不重要。但是必須選擇三個，然後將電流相對於電阻上的電壓極性放置。電流源所在的兩個分支不需要為它們建立額外的電流符號，就像電壓源不需要為它建立電壓符號一樣。

方程計數

我們被告知電阻和電壓源有值，因此應該被視為已知數。我們只是不知道具體的值是多少，所以我們必須用符號來解。

$R_{1}=\surd$
$R_{2}=\surd$
$R_{3}=\surd$
$R_{4}=\surd$
$R_{5}=\surd$
$I_{1}=\surd$
$I_{2}=\surd$
$V_{1}=\surd$
$i_{R1}=?$
$i_{R2}=?$
$i_{R3}=?$
$i_{R4}=?$
$v_{R1}=?$
$v_{R2}=?$
$v_{R3}=?$
$v_{R4}=?$
$v_{R5}=?$
$v_{I1}=?$
$v_{I2}=?$

共有 11 個未知數。由電阻可得 5 個方程，由迴路可得 3 個方程，由節點可得 3 個方程。因此，該問題可顯式求解。

端子方程

$v_{R1}=i_{R1}*R_{1}$
$v_{R2}=i_{R2}*R_{2}$
$v_{R3}=i_{R3}*R_{3}$
$v_{R4}=i_{R4}*R_{4}$
$v_{R5}=-I_{2}*R_{5}$
電流 $I_{2}$ 為負，因為它流入 $R_{5}$ 的負極。

當有多個電源時，方程式必須包含其電流方向或電源極性。

如果方向弄錯了，通常答案的大小會正確，但符號會錯誤。關鍵是答案非常相似。問題通常是符號約定以某種方式弄亂了。

環路方程

$L_{1}:v_{R2}+v_{R1}-V_{1}=0$
$L_{2}:v_{R3}+v_{R4}+v_{I1}-v_{R2}=0$
$L_{3}:v_{R5}+v_{I2}-V_{R4}=0$

電流源的電壓極性是任意選擇的，但必須做出選擇。必須在圖紙上記錄選擇，然後反映在方程式中。否則無法檢查方程式。

節點方程

$J_{1}:i_{R1}-i_{R2}-i_{R3}=0$
$J_{2}:i_{R3}+I_{2}-i_{R4}=0$
$J_{3}:i_{R4}-I_{2}-I_{1}=0$

求解方程組

代數

代數解法非常龐大、混亂，難以檢查，而且不會激發任何人的興趣。不會嘗試它。

微分方程

這個問題中沒有微分方程，但本課程四分之三的時間都在學習這種複雜電路，使用電容器和電感器而不是電阻器，並觀察微分方程。

符號計算

Mathematica

檔案：Ex5-6.png

Mathematica 解法。點選此處獲取要輸入 Mathematica 的文字。

無論方程的形式如何，Wolfram Alpha 都不支援超過 6 或 7 個方程。將在 Mathematica 中進行。然後在 MuPAD 中進行。然後比較答案。

MuPAD

檔案：Ex5-7.png

MathWorks MuPAD 解法 .. 點選此處獲取要剪下和貼上的文字 .. MuPAD 解法包含變數解

MuPAD 的答案與 Mathematica 相匹配，但更復雜答案的格式截然不同。然後目標是使用某種簡化命令，但可以使用替代符號來表達相同的答案。檢視 $V_{I2}$ 答案。它們相同，但它們使用不同的符號。

事實上，還有一個答案

$V_{I1}={\frac {(R_{1}+R_{2})}{R_{1}*R_{2}}}*({\frac {V_{1}}{R_{1}}}-I_{1})-R_{3}*I_{1}-R_{4}*(I_{1}+I_{2})$

檔案：Ex5-7r.png

使用簡化命令簡化的 Mathematica 解法 .. 看起來更接近 MuPAD 解法

使用簡化和擴充套件命令進行一些操作會有所幫助。與簡化命令相關的各種選項引入了符號計算的領域，這會使本課程的重點偏離。對於複雜表示式的求解，各軟體包之間還沒有達成一致意見。除 $V_{I1}$ 之外，所有內容的視覺檢查都是匹配的。

唯一其他快速檢查方法是代入一組隨機數，看看兩個解是否得出相同的數值解。但在這方面已經花費了足夠的時間。

數值解

由於沒有給出數字，所以不存在數值解。

模擬

沒有數字，模擬是不可能的。

建立直覺

• 複雜的表示式沒有符號計算一致同意的通用形式。因此，檢查它們是一個代數過程，或者可以相信，插入數字並顯示它們匹配意味著符號表達式是相同的。
• 當定義變數時，方向選擇暗示 $V_{1}$ 正在向電路中注入能量。觀察解，似乎 $I_{R1}$，即透過 $V_{1}$ 的電流是正的。因此，仍然是 $V_{1}$ 正在向電路中注入能量。
• 當定義變數時，方向選擇暗示 $I_{2}$ 正在向電路中注入能量。觀察解，似乎 $V_{I2}$，即跨過 $I_{2}$ 的電壓是正的。因此，仍然是 $I_{2}$ 正在向電路中注入能量。
• 當定義變數時，方向選擇暗示 $I_{1}$ 正在從電路中吸收能量併為其電池充電。然而，觀察解，似乎 $V_{I2}$，即跨過 $I_{1}$ 的電壓是負的。因此，看來實際上 $I_{1}$ 也正在向電路中注入能量。