電路理論/狀態變數

需要新的技術來解決二階及更高階電路

• 符號解太複雜，僅僅比較答案也是一個練習
• 解析解法更加零散
• 常數、初始條件和電路佈局之間的關係變得複雜

如果電路分析要

• 超越理想
• 考慮更復雜的電路
• 瞭解電路建模軟體的侷限性/近似值

解決方案是“狀態變數”。在狀態變數分析之後，透過消除對輸出影響不大的項，可以簡化建立符號解的過程。

狀態空間

電路理論的 狀態空間 方法放棄了電路分析的符號/解析方法。狀態變數模型涉及以矩陣形式描述電路，然後使用 級數展開、辛普森規則 和 克萊姆法則 等工具進行數值求解。這是 matlab 的最初起點。

狀態

“狀態”表示電路能量儲存元件的“條件”或“狀態”。由於電阻器不會改變（理想情況下）並且不儲存能量，因此它們不會改變電路的狀態。狀態是在時間上的一個快照，代表著電流和電壓。 “狀態空間”分析的目標是建立一種表示所有可能狀態的符號。

狀態變數

用於描述所有狀態的符號應該儘可能簡單。與其試圖找到一個複雜的、高階的微分方程，不如回到類似於 基爾霍夫分析 的東西，並只寫端子方程。

狀態變數是電容器兩端的電壓和電感器中的電流。這意味著純電阻電路的 割集 被合併成單個電阻器，最終與電感器串聯或與電容器並聯。與其使用符號 v 和 i 來表示這些未知數，不如將它們都稱為 x。使用基爾霍夫方程代替節點方程或迴路方程。端子方程被代入基爾霍夫方程，這樣剩餘電阻的電流和電壓就會與電感器和電容器共享。

狀態空間模型

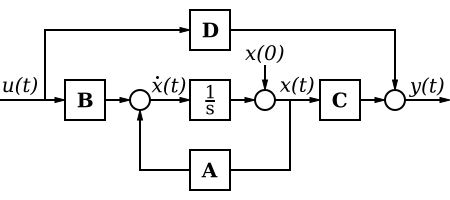
此狀態空間模型描述了輸入（階躍函式 μ(t)、初始條件 X(0)）、輸出 Y(t) 以及 A、B、C 和 D。A-B-C-D 是傳遞函式，它們以如下方式組合

${\frac {\mathbb {Y} }{\mathbb {\mu } }}=B(s)\left({\frac {1}{s-A(s)}}\right)C(s)+D(s)$

控制系統課程教導如何從所需的傳遞函式構建這些框圖。積分“記憶”或累積過去狀態的歷史。導數預測未來狀態，此外，當前狀態可以分別進行縮放。“A”表示反饋。“D”表示前饋。還有很多東西要學。

不要試圖弄清楚負號是如何出現在分母中的，以及附加項是如何出現的。上面是如何幫助我們預測電路中的電壓和電流？讓我們從定義術語並舉一些例子開始。

• A 是一個方矩陣，表示電路元件（來自基爾霍夫方程）。
• B 是一個列矩陣或向量，表示源如何影響電路（來自基爾霍夫方程）。
• C 是一個行矩陣或向量，表示輸出是如何計算的（可能是電壓或電流）
• D 是一個單一數字，表示源的倍數...... 通常為零，除非源直接透過電阻器連線到輸出。

A 和 B 一般描述電路。如果 X 是一個列矩陣（向量），表示所有未知的電壓和電流，那麼

${\boldsymbol {\dot {X}}}={\boldsymbol {A}}{\boldsymbol {X}}+{\boldsymbol {B}}{\boldsymbol {\mu }}$

此時，X 已知，表示時間函式的列。可以使用 C 和 D 從已知的 X 和原始階躍函式 μ 推匯出輸出

$y={\boldsymbol {C}}{\boldsymbol {X}}+D*{\boldsymbol {\mu }}$

MatLab 實現

檔案：MatLabSimulinkStateSpace.png

matlab 螢幕截圖，帶有 simulink 工具箱，顯示如何獲取用於華夏公益教科書電路分析的狀態空間塊

如果沒有像 MatLab 這樣的工具，這將不會是一個進步。這些是相關的 MatLab 控制系統工具箱命令

• step(A,B,C,D) 假設初始條件為零
• initial(A,B,C,D,X(0)) 與 step 相同，但考慮了初始條件 X(0)

此外，還有一個名為“狀態空間”的 simulink 塊，可以用相同的方式使用。

影片介紹

• 來自 digilent corp 的 41 分鐘介紹
• 5 分鐘電路應用

進一步閱讀

• 控制系統/狀態空間方程
• matlab 幫助連結