圓錐曲線/圓

圓是最簡單、最著名的圓錐曲線。作為圓錐曲線，圓是垂直於錐體軸的平面與錐體的交點。

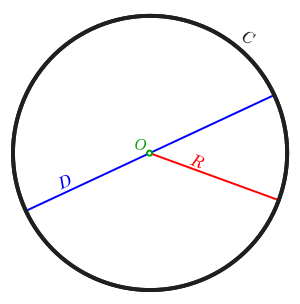
圓的幾何定義是所有點到一個固定點$(h,k)$的距離為一個常數$r$的點的軌跡，形成圓周 (C)。距離$r$是圓的半徑 (R)，點$O=(h,k)$是圓的中心。直徑 (D) 是半徑長度的兩倍。

圓的示意圖，圓周 (C) 為黑色，直徑 (D) 為青色，半徑 (R) 為紅色，中心或原點 (O) 為洋紅色。

方程

標準形式

以$(h,k)$為圓心，$r$為半徑的圓的標準方程是

$(x-h)^{2}+(y-k)^{2}=r^{2}$.

在圓心位於原點的最簡單情況下，該方程只是勾股定理的重新陳述

$x^{2}+y^{2}=r^{2}$

一般形式

圓方程的一般形式是

$x^{2}+y^{2}+2gx+2fy+c=0$，其中

<-g,-f> 是圓的圓心。

極座標

在圓心位於原點的圓的情況下，圓的極座標方程非常簡單，因為極座標本質上是基於圓的。對於半徑為$a$的圓，

$r=a$.

在圓心位於任意位置的更復雜情況下，該方程是

$r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}$,
其中$r_{0}$是圓心到原點的距離，$\varphi$是指向圓的角。

有許多情況允許簡化該方程。如果圓上的一個點與原點相切，則其極座標方程可能只包含一個三角函式。

.....

引數方程

當圓的方程用引數 $t$ 引數化時，方程變為

$x=h+r\cos t$,
$y=k+r\sin t$.

示例

找到以下圓的圓心和半徑：x²+y²+8x-10y+20=0 透過以下步驟

x²+y²+8x-10y+20=0
x²+y²+8x-10y= - 20
(x²+8x)+(y²-10y)= - 20
+16 +25 +16+25
(x²+8x+16)+(y²-10y+25)=21
(x+4)²+(y-5)²=21

因此
C(-4,5) 半徑=$radical(21)$