控制系統/示例/二階系統

二階系統：示例

掃雷船上指向水聽器陣列的阻尼控制系統，從傳動軸到陣列的開環傳遞函式如下。

G(s)={\frac {K}{Js^{2}+K_{d}s}}

增益引數 K 可以改變。陣列的慣性矩 J 和水對陣列的粘性阻力產生的力 K_d 是已知常數，給出如下

該系統被安排為具有單位反饋的閉環系統。找到 K 的值，使得當輸入為單位階躍時，閉環響應的過沖量最多為 50%（大約）。您可以使用標準響應曲線。為了減少過沖量，K 應該大於還是小於該值？
找到系統相應的時域響應。
現在，系統接收恆定角速度 V 的輸入。對於上面找到的 K 的極限值，計算 V 的最大值，使得陣列最多以 5° 的誤差跟隨輸入。

首先，讓我們繪製系統的框圖。我們知道開環傳遞函式，並且存在單位反饋。因此，我們有

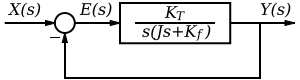
閉環增益由下式給出

$H(s)$	$={\frac {G(s)}{1+G(s)}}$
	$={\frac {\dfrac {K}{Js^{2}+K_{d}s}}{\dfrac {Js^{2}+K_{d}s+K}{Js^{2}+K_{d}s}}}$
	$={\frac {K}{Js^{2}+K_{d}s+K}}$

現在我們需要將閉環傳遞函式表示為標準二階形式。

${\frac {\omega _{n}^{2}}{s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}}}$	$={\frac {K}{Js^{2}+K_{d}s+K}}$
	$={\frac {\frac {K}{J}}{s^{2}+{\frac {K_{d}}{J}}s+{\frac {K}{J}}}}$

現在我們可以表示自然頻率 ω_n 和阻尼比 ζ

\omega _{n}^{2}={\frac {K}{J}}={\frac {K}{9}}

2\zeta \omega _{n}={\frac {K_{d}}{J}}

\zeta ={\frac {K_{d}}{2J}}{\sqrt {\frac {J}{K}}}={\frac {K_{d}}{2}}{\sqrt {\frac {1}{KJ}}}={\frac {1}{3{\sqrt {K}}}}

現在我們看看二階系統的標準響應曲線。

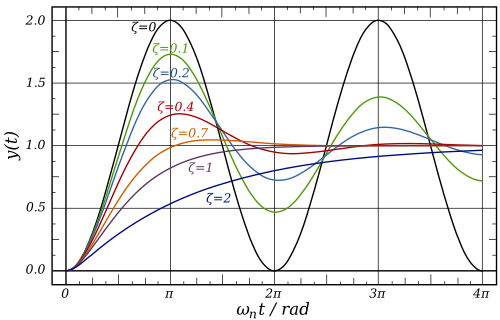
我們看到，對於 50% 的過沖，我們需要 ζ=0.2 或更大。

\zeta ={\frac {1}{3{\sqrt {K}}}}\geq {\frac {1}{5}}

K\leq {\frac {25}{9}}

這是允許的最大值，因此為了減少過沖，K 應該小於此值。現在我們可以完全評估自然頻率。

\omega _{n}={\frac {5}{9}}

二階系統的輸出由以下等式給出。

$y(t)$	$=1-{\frac {1}{\sqrt {1-\zeta ^{2}}}}e^{-\zeta \omega _{n}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t+\sin ^{-1}{\sqrt {1-\zeta ^{2}}}\right)$
	$=1-{\frac {1}{\sqrt {0.96}}}e^{-t/9}\sin \left({\frac {5{\sqrt {0.96}}}{9}}t+\sin ^{-1}{\sqrt {0.96}}\right)$
	$=1-1.02e^{-t/9}\sin \left(0.544t+0.436\pi \right)$