密碼學/基本公鑰示例

公鑰密碼學的基本工作原理最好用一個例子來解釋。下面的工作涵蓋了簡單金鑰的製作以及明文樣本的加密和解密。出於必要性，這個例子被大大簡化了。

基本公鑰摘要

公鑰加密用於網際網路安全連結，例如，當瀏覽器開啟銀行網站或使用信用卡的網站時。此類地址以 https 為字首，而不是僅僅使用 http。RSA-OpenSSL 就是這樣的加密系統。在這個安全網站標記的例子可以在本頁面的地址中看到；此華夏公益教科書頁面（當用戶登入時）顯示 https 字首或其他一些特定於瀏覽器的標記，表明它被認為是安全的。
每個網站都有自己的 加密金鑰 和 解密金鑰，分別稱為公鑰和私鑰。這些本質上都是非常大的數字。這些金鑰總是不同的，從而產生了 非對稱加密 的術語。實際上，每當我們說金鑰時，我們指的是一對組成金鑰的數字；一個用於冪運算的金鑰數字，另一個是用於該運算的模數。對於不熟悉模運算的人來說，請參閱華夏公益教科書頁面 高中數學擴充套件/素數/模運算，以獲得一個簡單易懂的描述。

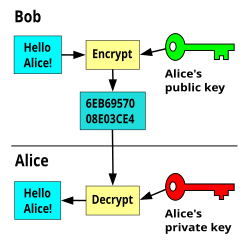
公鑰對任何人都公開可用，但私鑰則不公開。接收方站點將他的公鑰提供給訊息傳送方，或者透過使用公共目錄。對於每次訊息傳輸，傳送方都使用此金鑰來生成程式碼。這樣，只有接收方的私鑰才能解密它。在下面的文字中提供了一個實際的例子，並且可以在圖 1 中看到基本過程。
實際上，用於公鑰加密的兩個金鑰形成一個 可逆函式。如果系統設計者打算這樣做，你也可以用私鑰加密，用公鑰解密。當然，對於不那麼公開的使用，公鑰也可以像私鑰一樣被保密。這種金鑰對的可逆性在測試數字證書時很有用，其中頒發者用他的私鑰加密證書，以便接收者可以用他公開的公鑰來測試其真實性。
使用的數字被故意設定得非常大，這使得從公鑰中獲取私鑰的任務對於駭客來說過於困難。它涉及對非常大的數字進行因式分解，非常耗時。
這類系統雖然不完美，但只要破解它們所需的時間遠遠超過資料感興趣的期限，它們仍然很有用。估計破解某些此類程式碼所需的時間是數千年。
簽名的數字證書在提供公鑰時有助於驗證使用者站點的身份。瀏覽器會採取步驟來確認其有效性。
公鑰系統的主要優點是管理負擔很低。傳送訊息到站點所需的一切資訊都可以在公共目錄中找到，或者作為建立連結的一部分公開發送。
公鑰密碼學的主要缺點是它對於現代網際網路使用來說太慢了。因此，網際網路最常使用 對稱加密 來完成主要任務；（一種不同的方法，它使用一個共同的金鑰來進行加密和解密）；它只是使用公鑰方法來隱藏對稱金鑰，同時將其傳送到遠端。
駭客使用多種方法來破解編碼
- 暴力破解 金鑰指的是嘗試私鑰的所有可能組合，同時將其與相關的密文進行測試。這種測試非常耗時，因為每次迭代都需要字典檢查或人工干預來決定是否出現了明文。此外，數字非常大，因此這種方法很少有什麼意義。
- 數學攻擊指的是找到兩個素數，它們的乘積構成了公開可用的金鑰的模數。如果能夠找到它們，那麼它將簡化私鑰的查詢（稍後詳細介紹）；這種方法的優點是計算機可以自主完成這項任務，不需要太多幹預。截至撰寫本文時（2014 年），Lenstra 等人打破金鑰的數學攻擊的記錄是 2009 年 12 月 12 日，當時一個 RSA-768 位模數（232 個十進位制數字）被使用一種叫做一般數域篩法（GNFS）的方法進行分解。這個過程需要兩年的合作以及數百臺計算機。（參見：http://eprint.iacr.org/2010/006.pdf）如今，大多數使用的加密金鑰遠大於被破解的那個，一個 1024 位或 2048 位的 SSL 證書金鑰仍然被認為對數學攻擊是相當安全的。請注意，破解此類金鑰的難度隨著金鑰長度的 指數級 增加。
- 然而，成功的入侵歷史並沒有涉及程式碼破解，而是駭客入侵伺服器以獲取其資料和私鑰。其他利用漏洞依賴於個人的安全疏忽或程式缺陷。例如，最近的一次 SSL 利用漏洞（2000-2014 年？），其訪問資料並不是透過程式碼破解，而是透過一個程式缺陷，該缺陷允許傳送方從接收方的伺服器下載記憶體塊內容。SSL 的目的是允許接收方伺服器的一些文字作為訊息接收和成功解密的證明返回。為此，傳送方可以指定要返回的文字長度，通常是頭部，在任何情況下都小於 64K 位。該缺陷的核心在於，如果傳送了一個非常短的訊息，但傳送方要求返回比傳送的訊息更大的塊，則有缺陷的程式會照做，因此返回了包含其他安全材料的資料。每隔幾秒重複此過程，允許駭客積累大量資料塊。據說這個問題已經得到糾正，但據說在約四年的時間裡，任何知道它的人都可以利用它。

建立站點 B 的公鑰

公鑰對所有人公開，用於加密傳送給金鑰所有者的訊息.

每個站點的計算機都會生成兩個非常大的素數，由於它們是所有後續操作的基礎，因此這些數字永遠不會向任何其他人透露。（素數是指除了自身和 1 之外沒有其他因子的數字）。
這兩個數字相乘得到所有站點計算中使用的模數。主要公鑰也是從這些素數中推匯出來的，並確定明文數字將被提升到的指數。
此公鑰在目錄和證書頒發機構中提供，因此當傳送方想要透過公鑰密碼學加密訊息時，他可以輕鬆地使用 接收方 的公鑰（和模數）來實現。每個站點的公鑰集都可以被設計為幾乎肯定與其他所有站點不同。

為了說明這一點，讓我們用非常小的數字來代替大型素數，為想要接收訊息的人建立一個簡單的例子。

假設兩個秘密持有的素數是

p = 5  ,  q = 11

那麼將被使用的運算的模數由它們的乘積給出

m = 5  x  11 = 55    (the modulus of the arithmetic to use)

加密金鑰的計算方法如下：首先，使用這兩個素數，計算函式

   f(n)  = (p-1) x (q-1)
∵ p = 5 and q = 11    
∴ f(n) = (5-1) x (11-1)
∴ f(n) =  40

然後，
選擇任何一個與 f(n) 互質且小於它的數字。

（當兩個數字除了 1 之外沒有其他公因子時，它們被稱為互質。此術語也稱為互質或互素）。

 The possible choices become:
 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31, 33, 37, and 39.

 Say we select the public encrypt exponent =  7

然後，接收方站點的公鑰可以安全地釋出給全世界，即

(7, 55) as (encryption exponent, modulus)
(In practice the numbers would be very much larger)

實際使用的數字非常大。例如，對於 1024 位的 RSA 加密，此數字是模數的位數；這相當於大約 308 位的十進位制數，或 256 個十六進位制數字。最常選擇的公共指數具有 65537 的整數值。選擇此指數是因為它比其他一些選擇產生更快的加密速度；也就是說，由於它在二進位制形式中的大量零計數（10000000000000001），它適合使用二進位制移位方法進行快速處理。它在別處被稱為費馬數 F4。儘管人們偏愛相同的指數，但請記住，公鑰集的另一部分是模數，而模數將因使用者而異，因為可用的素數數量非常多。

建立站點 B 的私鑰

站點 B 在解密傳送給它們的訊息時使用，該訊息使用站點 B 的公鑰加密.

私鑰對用於解密訊息，並且只有當使用同一站點的公鑰加密訊息時，此金鑰才有效。也就是說，站點 B 的公鑰是從目錄中獲取的，然後由站點 A 用於加密傳送給它們的訊息。當訊息到達站點 B 時，站點 B 使用它自己的私鑰進行解密。

繼續以上面的簡單示例，站點 B 的私鑰是從其公鑰中生成的，方法如下。

   私鑰解密指數 = (公鑰加密指數)-1 Mod f(n)
∵ 公鑰加密指數 = 7， 且 f(n) = 40
∴ (私鑰解密指數 x 7) Mod 40 = 1
∴ 私鑰解密指數 = 23


  站點 B 的私鑰對是：
  (23, 55) 作為 (解密指數，模數)

有些人可能已經注意到，加密指數和解密指數可以是相同的數字。這種情況必須透過刻意測試來避免，因為駭客很可能在攻擊過程的早期測試這種可能性。在上面的例子中，如果選擇 9、11、21、33 或 39 作為公鑰，而不是其他數字，就會出現這種情況。不要以為預測這種錯誤很簡單，請注意，即使在這種情況下，既是互素數又是素數的互素數（例如：導致：11 * 11 = 1 mod 40），以及那些互素數但本身不是素數的互素數（例如：9、21、33 和 39），都可能導致這種不安全的狀況。

使用長素數時，模數 (m)（它們的乘積）會長得多，但很明顯，如果駭客能夠找到兩個秘密素數作為起點，他仍然可以獲得私鑰。公鑰和與之一起使用的模數都提供給所有需要它進行加密的人，因此數學攻擊的負擔就減少到將模數分解成這兩個秘密素數的難度。對於上面顯示的簡單示例 (m=55)，這項任務非常簡單，但對於非常大的數字，這項工作就很長，讓人望而卻步。

私鑰的原生格式實際上是 base-64（一種字元集，每個字元只需要 6 位，而不是十六進位制的 4 位或 ASCI 字元程式碼的 7 位）。與公鑰字串不同，1024 位 RSA 加密的實際私鑰字串的佈局包含私鑰詳細資訊、公鑰詳細資訊以及生成它們時使用的秘密數字，以及其他一些數字和標頭。私鑰指數與公鑰指數不同，它很長，相當於 256 個十六進位制數字的長度。兩個秘密素數分別是 128 個十六進位制數字的長度。十進位制等效長度為私鑰指數（和模數）的 308 位，以及每個秘密數字的 154 位。

對模數進行因式分解

駭客想要在沒有任何其他演算法輔助的情況下對模數進行因式分解，他們可以簡單地用一系列遞增的素數除以模數，直到餘數為零。然後，兩個素數就知道了。但是，在如此大的模數中，素數的數量也非常多。一般來說，以下近似值，稱為素數定理，給出了數字 x 中素數的數量為

   素數的數量 ≅ x/(logx - 1)
   現在，64 位空間相當於大約 20 位數字
∴ 素數的數量 ≅ 4 * 1017
   然後假設每秒 100 萬次計算（對於大多數人來說，這是一個非常樂觀的假設）
   測試所有素數的時間 ≅ 13,500 年

這裡給出的示例僅限於 64 位，因為更具代表性的數字（128 位、256 位、512 位、1024 位和 2048 位計算）對於大多數計算器來說都太大。請參閱 DigiCert 的 破解 2048 位證書背後的數學原理，以瞭解更多詳細資訊。

此示例不考慮使用改進的因式分解方法，而這些方法在文獻中經常出現。目前（2014 年），這些方法中最好的是通用數域篩法 (GNFS)，用於建立 2009 年 12 月的記錄.

為了更詳細地說明改進方法，很明顯，從表格素數列表開始可以加快處理速度。這一點，以及針對未來需要計算出的乘積表，也能比在執行時進行計算快得多。因為很明顯，對於大量此類破解問題，一半的解將位於嘗試值的前半部分，一半位於後半部分，所以習慣上將對整個集合隱含的素數定理所隱含的一半集合的預期解決時間表達為一半。

使用 B 的公鑰進行加密

假設公鑰對屬於站點 B。還假設由數字“2”表示的明文字元要由站點 A 加密併發送給收件人站點 B：站點 A 使用站點 B 的公鑰對進行加密。

   假設明文=2
   密文 = 明文公鑰加密指數 Mod n
∵ 公鑰加密指數 =7， 模數 = 55
∴ 密文 = 27 Mod 55 = 128 Mod 55
∴ 密文 = 18

使用示例中使用的非常小的數字，破解程式碼將相對簡單。但是，對於素數p和q的非常大的值，並且在不知道私鑰的情況下，這項工作變得非常困難。在某些情況下，即使對於大量計算機來說，這項任務也需要相當長的時間。

公鑰加密不會掩蓋所用字元的相對頻率。由於這會提高破解程式碼的可能性，因此被認為是此類系統中的一個缺陷。因此，明文字元在加密之前被排列成組以隱藏它們的使用頻率；這些組非常大，限制是加密的數字的大小必須小於正在使用的模數。

使用 B 的私鑰進行解密

使用上述特定示例進行解密的方法如下：對於接收到的密文 = 18

   對於來自上一節的密文=18
   明文 = 密文私鑰解密指數 Mod n
∵ 私鑰解密指數 = 23， 模數 = 55
∴ 明文 = 1823 Mod 55 = 74347713614021927913318776832 Mod 55
∴ 明文 = 2（你只能用 Windows 科學計算器來確認這一點）

請注意，明文值2已恢復，這是所需的結果。

例外情況

一些使用非正確私鑰的嘗試仍然會成功。需要考慮例外情況。例如，在上述情況下，使用解密指數 =3 也會產生正確的結果。見下文

   對於來自上一節的密文=18
   明文 = 密文私鑰解密指數 Mod n
∵ 駭客嘗試的解密指數 = 3， 模數 = 55
∴ 明文 = 183 Mod 55 = 5832 Mod 55
∴ 明文 = 2 也是正確的結果。
請注意，每個 (N^7Mod55)^3Mod55 == (N^7Mod55)^23Mod55)

在實際環境中，在選擇金鑰時，需要進一步考慮此類問題。

網際網路速度折衷方案

由於公鑰加密和解密非常慢，因此它們不適合以其原生形式用於網際網路。事實上，非對稱公鑰加密僅用於網際網路通訊的一小部分。此類系統是混合系統。所使用的方法的總結如下

要安全傳輸的文字不是透過公鑰密碼術進行加密的，而是透過使用對稱金鑰加密進行加密的。這通常是 128 位密碼，但可以更大。對稱金鑰方法需要兩個站點使用相同的金鑰。為此，一個站點必須在某個階段生成金鑰，然後將其副本傳送到另一個站點。
此對稱金鑰不是公開發送到遠端，而是首先使用公鑰方法對其進行加密後保持安全。為此，將使用目標站點的公鑰。
接收者使用其私鑰解密此密文，並恢復對稱金鑰值。然後，他用它解密主對稱密文。
對稱加密金鑰在當前會話結束時被丟棄，而非對稱公鑰可能會被丟棄，也可能不會被丟棄，這取決於所使用的系統。金鑰的較短壽命可以減少網路攻擊期間成功恢復金鑰的可能性，以及隨後在較晚時間對記錄的流量進行解碼的可能性。考慮到這一點，短會話可能比長會話更安全，當然前提是丟棄意味著從記憶體中完全刪除，而不僅僅是普遍的刪除。

目前用於網際網路瀏覽器的系統是傳輸層安全 (TLS) 及其前身安全套接字層 (SSL)。在維基百科的 安全套接字層中可以找到這些內容的完整描述。

請注意，在雙工系統中，即通常的雙向傳送系統，將有兩種這樣的過程。一個起源於每端。用於傳送和接收的金鑰集（對於非對稱和對稱加密系統）都是不同的。

訊息認證

如果外部人員可以在傳輸過程中更改訊息，或者從一開始就錯誤地代表自己，安全性就會崩潰。為了克服這些風險，數字證書被設計出來。為了進一步確保證書來自使用者尊重的機構，證書被賦予了數字簽名。在眾多方法中，一種方法是數字簽名演算法 (DSA)，它是數字簽名標準 (DSS) 的基礎。

這些證書不僅僅是簡單的文字訊息，當然可以被模仿，而是使用基於訊息內容的計算值。認證的整個基礎依賴於這些雜湊演算法的設計屬性以及斷言其價值的人的完整性。它們的屬性包括

敏感性：它們非常敏感。雜湊演算法輸入的微小變化總會對其輸出值產生非常大的變化。
特異性：它們非常特定。雖然這取決於使用的雜湊演算法，但兩種不同的輸入幾乎不可能產生相同的輸出。當這種情況發生時，例如每數十億次發生一次，它被稱為衝突。
不透明性：無法從輸出值中找到輸入值。這是因為演算法的高度複雜性，尤其是因為大量使用了模算術的單向函式。
保密性：一些雜湊演算法可供公眾使用，但專有利益可以建立自己的演算法。大多數人可以使用的一些演算法包括 MD5、SHA1、SHA2、SHA3 等。MD5 已經被破解。SHA1 是當前大多數證書的基礎，已被棄用，因為它在使用上過於複雜。

雜湊值由傳送方計算，並與接收端計算的值進行比較，兩者必須匹配才能被接受。與加密本身一樣，雜湊值難以逆向工程，也就是說，外部人員無法在任何有用的時間段內建立新的或更改的訊息來表示現有的雜湊值。因此，它們提供了驗證訊息內容自證書釋出以來未更改的基礎。

證書本身會根據瀏覽器儲存區中已知的根證書進行測試，以確保證書來自已知的可靠來源。如果證書使用僅發行機構知道的私鑰進行秘密簽名，則可以透過使用其公鑰解密簽名來驗證證書。也就是說，由於該過程是可逆的，因此可以驗證來源。

用於這些任務的實際過程比摘要中暗示的要複雜得多，涉及許多長位計算，但該系統的強度可能無法滿足懷疑者的要求，直到看到這些計算。請參閱 PDF 檔案 加密和數字簽名工作原理 並閱讀數字簽名機制示例部分以獲取此類描述。

證書測試和其他事項的處理過程通常由瀏覽器為使用者總結。瀏覽器將清楚地指示它們是否認為連線是安全的。這些指示中最常見的是在螢幕上的某個位置新增一把鎖，並將網站的http 地址標題修改為https。一些瀏覽器，如 Opera，還會新增其他資訊，例如顏色編碼，以表示安全級別。

另見

高中數學擴充套件/素數/模算術 : 你可能已經忘記的東西。

進一步閱讀

仿生水牛技術說明 35：加密和數字簽名工作原理 清晰地描述了資料加密標準 (DES)、RSA 公鑰標準和數字簽名演算法 (DSA) 的工作原理，並附有豐富的數學說明。
數字簽名演算法
破解分解記錄 : DigiCert 對破解 2048 位證書的估計背後的數學原理。
RSA 分解挑戰: 包含迄今為止在素數分解方面的進展表。
RSA 金鑰佈局: 顯示 1024 位 RSA 加密的私鑰和公鑰的精確佈局的頁面。