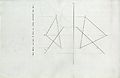
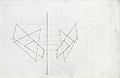
描述幾何/穿刺點
穿刺點是非平行線穿過並與平面相交的點。它們定義了直線與平面相交的平面上的位置。
A) 直線和平面 相交形成一個點,直線穿過平面。


解決方法
- 邊緣檢視法
- 切割平面法
使用邊緣檢視法
1) 找到平面中與折線平行的正面檢視的水平線。
2) 將直線投影到頂檢視中。(真實長度線)
3) 透過將真實長度線視為點檢視,找到平面的邊緣檢視。(建立一個垂直於真實長度線的折線)。
4) 邊緣檢視和給定直線之間的部分將是穿刺點。將該點投影回頂檢視和正面檢視。
問題
解決方案
使用切割平面法
1) 確定一個檢視並使用直線與平面接觸的點來定義切割平面
2) 將這些點投影到下一個檢視中。
3) 連線這些點以獲得切割平面的軌跡。
4) 軌跡線與給定直線相交的地方是直線穿過平面的穿刺點。
問題
解決方案
問題
1) 確定用作切割平面的直線。(兩個不同的切割平面有兩個不同的直線)
2) 對兩條直線執行切割平面法
3) 連線找到的兩個穿刺點 - 這就是交線。
4) 確定可見性
透過解決下面的平面和平面相交問題來練習。
問題 1
解決方案 1
二面角是兩個平面相交時形成的銳角。
1) 在找到交線後,建立一個輔助檢視,其中交線是真實長度。
2) 然後建立一個另一個輔助檢視,其折線垂直於真實長度線。
3) 在此檢視中,真實長度線將被視為一個點,而兩個平面將被視為邊緣
4) 測量兩個平面邊緣之間的二面角。
- 可以使用旋轉來減少所需的輔助檢視數量。
_______________________________________________________________________________________________________________________________________
C) 直線和實體 - 當直線與實體相交時,使用直線作為平面的邊緣檢視,在實體中建立一個截面;使用截面平面上的點將其轉移到實體檢視中。在切割平面上的點與另一個檢視中的直線相交的地方,您將獲得穿刺點。

示例問題]]

示例問題]]
-
穿刺點問題 #1

_________________________________________________________
______________________________________________________________________________
D) 平面和實體 - 根據您要相交的實體,定位穿過實體的相交平面上存在的穿刺點。這可以基於切割平面法,或者對於圓錐體和圓柱體,確定特定於形狀的穿刺點。
_____________________________________________________________________________________________________________________________________
E) 實體和實體 - 當兩個實體相交時,可以透過首先使用穿刺點來找到兩個實體的兩個面相遇的位置來找到相交點。(角形實體需要在頂點處的穿刺點,而圓形實體需要圍繞實體曲線的多個任意點。
透過解決下面的實體和實體問題來練習。
問題 1
解決方案 1
_________________________________________________________________________________________________________________________________________
可見性- 確定實體、直線或平面的前後順序。
1) 在找到穿刺點後,確定一個檢視。(例如,頂檢視)
2) 將穿刺點向下投影到另一個檢視中。(例如,正面檢視)
3) 確定投影線首先與哪個幾何物件相交。這是位於頂部(或最靠近圖形)的物件。在第一個檢視中。(例如,頂檢視。)\