數位電路/邏輯運算

數位電路

在上一章中，我們學習了什麼是數字資訊。數字資訊用位元表示，可以取 1 或 0 的值。在本章中，我們將開始探討如何使用數字資訊進行計算和其他操作。

我們即將討論的許多內容都是由喬治·布林 (1815-1864) 在其 1854 年發表的論文 思想規律探究，邏輯與機率數學理論的基礎 中正式化的。當時它幾乎沒有應用，但最終科學家和工程師意識到他的系統可以用來建立高效的計算機邏輯。涉及數字邏輯的數學分支被恰當地命名為布林代數。

基本運算子

數字邏輯有三個基本運算子，與、或和非。這三個運算子構成了數字邏輯中一切的基礎。事實上，您計算機執行的幾乎所有操作都可以用這三個運算來描述。幸運的是，這些運算並不難理解，因為它們的含義類似於日常語言中這些詞的含義。

與

與運算子的符號是一個點。使用與的數學表示式如下所示。

$A\cdot B$

與的另一種表示法是 $AB,A*B,A$ && $B$ 和 $A\land B.$ 只有當兩個輸入值都為 1 時，與表示式的值為 1。否則，值為 0。也就是說，只有當 A **和** B 為 1 時，上述表示式才等於 1。與運算子可以用以下真值表來描述。

$A$	$B$	$A\cdot B$
0	0	0
0	1	0
1	0	0
1	1	1

或

或運算子的符號是加號。使用或的數學表示式如下所示。

$A+B$

或的另一種表示法是 A $\vee$ B、A 或 B 以及 A || B。只有當兩個輸入值都為 0 時，或表示式的值為 0。否則，值為 1，也就是說，只有當 A 和 B 為 0 時，上述表示式才等於 1。或運算子的真值表

$A$	$B$	$A+B$
0	0	0
0	1	1
1	0	1
1	1	1

非

非是一個一元運算子，只需要單個輸入，而與和或是二元運算子，因為它們需要兩個值作為輸入。非運算子的符號。 ${\overline {A}}$ 或 **A'**

非表示式的值為輸入值的相反值。

$A$		${\overline {A}}$
0		1
1		0

與非和或非

如果將與、或和非運算子組合起來，就可以建立或非和與非

A 與非 B 是 ${\overline {A\cdot B}}$ 。這就是與門的反轉輸出。
A 或非 B 是 ${\overline {A+B}}$ 。這只是或門的反轉輸出。

與非

或非

Q={\overline {X\cdot Y}}

Q={\overline {X+Y}}

X	Y	Q
0	0	1
0	1	1
1	0	1
1	1	0

X	Y	Q
0	0	1
0	1	0
1	0	0
1	1	0

異或 (XOR) 和異或非 (XNOR)

另外兩個重要的門是異或門和異或非門，分別用 XOR 和 XNOR 表示。這有時用一個圓圈中的加號表示。

A XOR B 是 ${\overline {A}}\cdot B+A\cdot {\overline {B}}=A\oplus B$ 。只有當輸入中只有一個為 1 時，此結果才為真。
A XNOR B 是 ${\overline {{\overline {A}}\cdot B+A\cdot {\overline {B}}}}={\overline {A\oplus B}}$ 。這是異或門的反轉輸出：只有當兩個輸入相同的時候才為真。

XOR

XNOR

Q={X\oplus Y}

Q={\overline {X\oplus Y}}

X	Y	Q
0	0	0
0	1	1
1	0	1
1	1	0

X	Y	Q
0	0	1
0	1	0
1	0	0
1	1	1

XOR 代表模 2 加法，這意味著如果你將 1 加到 1，你將回到 0。這是數位電子學中非常有用的函式，但在布林代數中它不是一個重要的概念。

形式數學運算子

在邏輯領域（它是離散數學的一部分），存在一種與我們所見過的加法/乘法型別不同的符號表示法。

AND 用 $\wedge$ 表示。因此A AND B將被寫成 $A\wedge B$ 。
OR 用 $\vee$ 表示。因此A OR B將被寫成 $A\vee B$ 。
NOT 用 $\lnot$ 表示。因此NOT A是 $\neg A$ 。

不幸的是，計算機科學、工程學和數學似乎無法達成共識，因此我們必須同時使用兩種符號表示法。其他書籍，尤其是那些更側重於純邏輯或離散數學的書籍，可能使用各種不同的符號表示法，因此如果查閱其他書籍，則需要了解其他符號表示法。由於這是一本工程學書籍，我們不會使用這種符號表示法。

布林代數定律

布林代數與普通代數一樣，也遵循一定的規則。這些規則是結合律、分配律、交換律和德摩根定律。結合律、交換律和分配律只適用於 AND 和 OR 運算子。其中一些定律可能看起來很瑣碎，因為你已經習慣了它們。然而，當布林代數被建立時，它擁有不同的規則，我們認為“正常”代數中理所當然的每一個公理都無法保證適用。這些定律已被證明在布林代數下成立。

結合律

維基百科在 結合律 中有相關資訊

結合律是代數中的一種性質，表示項的求值順序無關緊要。

A+(B+C)\iff (A+B)+C\,

A\cdot (B\cdot C)\iff (A\cdot B)\cdot C\,

分配律

維基百科在 分配律 有相關資訊

分配律是指運算子可以應用於括號內的每個項。

A\cdot (B+C)\iff (A\cdot B)+(A\cdot C)\,

A+(B\cdot C)\iff (A+B)\cdot (A+C)\,

交換律

維基百科在 交換律 有相關資訊

交換律是指運算子應用的順序無關緊要。

A\cdot B\iff B\cdot A\,

A+B\iff B+A\,

德摩根定律

維基百科在 德摩根定律 有相關資訊

德摩根定律是 NOT 或非運算子不是分配律的結果。

{\overline {P\cdot Q}}\iff {\overline {P}}+{\overline {Q}}

{\overline {P+Q}}\iff {\overline {P}}\cdot {\overline {Q}}

德摩根定律（以奧古斯都·德·摩根 (Augustus De Morgan)，1806 年至 1871 年命名）告訴我們：一個與非門給出與輸入取反的或門的相同輸出；一個或非門給出與輸入取反的與門的相同輸出。這些輸入取反的門也稱為氣泡門，因為它們在符號上的表示方式，即在每個輸入上新增一個小的“氣泡”，就像在 NOT、NAND 和 NOR 門的輸出上畫圓圈一樣。

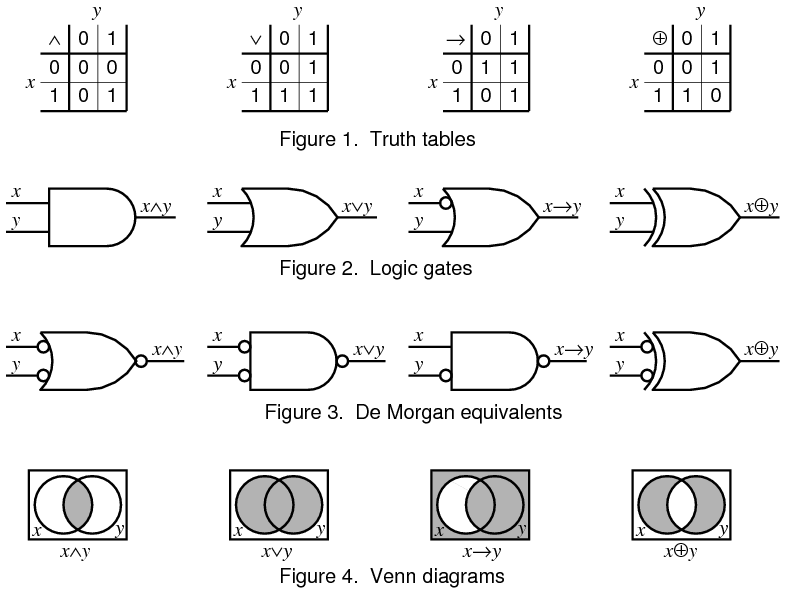
德摩根定律在簡化布林表示式時最有用。記住這些定律的一種簡單方法是“改變符號，打斷線”。

(練習索引)

練習

透過構建適當的真值表，驗證以下定律：

與運算子的結合律，
或運算子的分配律，
或運算子的交換律，
與非運算子的德摩根定律。

解答

我們看到以下的真值表

運算子優先順序

重要的是要注意

A\cdot B+C\neq A\cdot (B+C)

這可以看作是 AND 具有更高的優先順序，或者與和或之間不滿足結合律，或者是對分配律的無效應用。

從另一個角度來看，這是我們對普通代數的理解的應用，其中將或類比於加法，將與類比於乘法。如果這是用數字而不是布林實體的普通代數，我們永遠不會犯這個錯誤。

其他規則

所有這些定律都導致了許多適用於所有布林表示式的規則。這些定律有名字，但重要的是你能夠在需要的時候應用它們！請注意，許多規則有兩種形式 - 這稱為對偶性，我們將在後面討論。

	名稱	規則
1a	冪等律	$A\cdot A=A\,$
1b	冪等律	$A+A=A\,$
2a	恆等律	$A+0=A\,$
2b	恆等律	$A\cdot 1=A\,$
3a	有界性	$A+1=1\,$
3b	有界性	$A\cdot 0=0\,$
4a	補定律	$A+{\overline {A}}=1\,$
4b	補定律	$A\cdot {\overline {A}}=0\,$
5a	吸收律	$A+(A\cdot B)=A\,$
5b	吸收律	$A\cdot (A+B)=A\,$
6	對合律或雙重否定律	${\overline {\overline {\,A}}}=A$
7a	一致性定理	$A\cdot B+{\overline {A}}\cdot C+B\cdot C=A\cdot B+{\overline {A}}\cdot C$
7b	一致性定理	$(A+B)\cdot ({\overline {A}}+C)\cdot (B+C)=(A+B)\cdot ({\overline {A}}+C)$