數字訊號處理/數字濾波器

數字訊號處理

數字濾波器可以是非常複雜的裝置，但它們必須能夠對映到濾波器設計的差分方程。這意味著，由於差分方程只有有限數量的操作可用（加法和乘法），數字濾波器也只有有限的操作需要處理。數字濾波器只有少數幾個基本元件，儘管這些元件可以以複雜的方式排列以建立複雜的濾波器。

數字濾波器型別

數字領域中有兩種型別的濾波器：有限脈衝響應（FIR）濾波器和無限脈衝響應（IIR）濾波器。它們本質上截然不同。

FIR 濾波器

FIR 濾波器是取樣系統的特有濾波器。連續時間系統中沒有等效的濾波器。因此，只有非常特殊的模擬濾波器能夠實現 FIR 濾波器。

如果我們將離散時間衝激函式定義為

\delta [n]={\begin{cases}1&n=0\\0&n\not =0\end{cases}}{\mbox{,}}

FIR 濾波器對 δ[n] 的響應，記為 h[n]，將在有限數量的樣本後衰減為零。FIR 濾波器的傳遞函式只包含零點，或者沒有極點，或者只有位於原點的極點。

具有對稱係數的 FIR 濾波器保證提供線性相位響應，這在某些應用中非常重要。然而，FIR 濾波器的效率較低，要建立滿足給定規格的 FIR 需要比等效 IIR 濾波器多得多的硬體。

IIR 濾波器（無限脈衝響應濾波器）

IIR 濾波器通常基於連續時間傳遞函式設計。IIR 濾波器不同於 FIR 濾波器，因為它們始終包含電路中的反饋元件，這使得傳遞函式更難處理。

IIR 濾波器的傳遞函式包含極點和零點。它的衝激響應永遠不會衰減為零（儘管它可能非常接近零，以至於響應無法用系統中可用的位數表示）。

IIR 濾波器在計算方面提供了非凡的好處：IIR 濾波器的效率比等效 FIR 濾波器高一個數量級以上。儘管 FIR 濾波器更容易設計，但 IIR 濾波器可以用更少的元件完成相同的工作，更少的元件直接轉化為更少的成本。

在 Octave/Sciplot 中對時間序列進行濾波

首先為時間序列建立一些點。在本例中，我們將建立以 44 kHz 取樣的一秒鐘隨機資料。

sampling_t = 1/44000;
t = 0:sampling_t:1;
x = rand(size(t));

檢視時間序列

plot(t,x);

檢視它的頻譜（它大多是均勻的，這是我們對噪聲的預期結果）

specgram(x)

現在，我們將使用內建函式建立一個截止頻率為 pi*0.1 弧度的三階巴特沃斯低通濾波器

[b,a] = butter(3,0.1)

現在對時間序列進行濾波。

y = filter(b,a,x);

檢視濾波後資料的首 100 個點。

 hold on
 plot(y(1:100))
 plot(x(1:100))
 hold off

檢查它的頻譜圖

 specgram(y)

現在檢視 FFT 的幅度

 plot(log(abs(fft(y))))

濾波器響應型別

高通和低通

高通和低通濾波器是最簡單的數字濾波器形式，它們相對容易設計到規格。本頁將討論高通和低通傳遞函式，以及每種傳遞函式作為 FIR 和 IIR 設計的實現。

帶通

帶通濾波器就像高通濾波器和低通濾波器的組合。只有特定頻帶允許透過濾波器。過高或過低的頻率將被濾波器抑制。

阻帶

陷波濾波器是帶通濾波器的補充，它只抑制特定窄頻帶的頻率資訊，並允許所有其他資料毫無問題地透過。

陷波

帶通濾波器的直接補充稱為帶阻濾波器。陷波濾波器本質上是一個非常窄的帶阻濾波器。

梳狀濾波器

梳狀濾波器顧名思義，看起來像一把梳子。它們有很多“齒”，本質上是在傳遞函式中資訊被去除的陷波。這些陷波均勻地分佈在整個頻譜中，因此它們只對消除以規則頻率間隔出現的噪聲有用。

全通

全通濾波器是一個對所有頻率具有單位幅度響應的濾波器。它不影響系統的增益響應。全通濾波器確實會影響系統的相位響應。例如，如果設計 IIR 濾波器以滿足規定的幅度響應，系統的相位響應通常會變得非線性。為了校正這種非線性，將全通濾波器級聯到 IIR 濾波器中，以便整體響應（IIR+全通）具有恆定的群延遲。

典型和非典型

正則濾波器是指傳遞函式的階數與濾波器中延遲單元數量相同的濾波器。相反，非正則濾波器是指濾波器中延遲單元數量多於傳遞函式的階數的濾波器。一般來說，FIR 濾波器是正則的。一些 IIR 濾波器實現是非正則的。

以下是一個 2 階正則濾波器的例子。

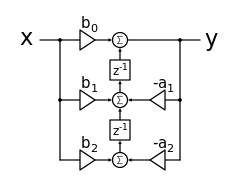
以下是一個 2 階非正則濾波器的例子。

注意，在正則濾波器中，系統階數（這裡為 2）等於濾波器中的延遲單元數量（2）。在非正則版本中，系統階數不等於延遲單元數量（4 個延遲單元）。兩種濾波器執行相同的功能。正則版本在數字硬體上更小，因為它使用的延遲單元更少。然而，如果級聯多個二階 IIR 濾波器，這種缺點幾乎消失，因為它們可以共享延遲單元。在這種情況下，唯一的“額外”延遲單元是第一級輸入側的那些。

符號

我們將使用一些基本符號。

ω_p 通帶截止頻率

ω_s 阻帶截止頻率

δ_p 通帶紋波峰值幅度

δ_s 阻帶紋波峰值幅度

← 快速傅立葉變換 (FFT) 演算法

數字訊號處理

FIR 濾波器設計 →