數字訊號處理/Σ-Δ調製

Σ-Δ調製器 (ΣΔ 調製器) 允許透過一位訊號進行模擬到數字轉換 (ADC) 或數字到模擬轉換 (DAC) 操作。

脈衝寬度調製 (PWM) 也使用一位訊號，但信噪比 (SNR) 更差，但切換速度更慢。

一階調製器

電路

一階 ΣΔ 調製器由累加器和比較器組成。

調製器 - 一階 - 數字

輸出是一個位元流，原始訊號可以透過低通濾波器重建。

分析

可以透過用誤差訊號的加法替換比較器來分析 Σ-Δ 調製器的頻率響應。

${\begin{array}{ccl}z\cdot acc&=&X+acc-Y\\Y&=&acc+E\end{array}}$

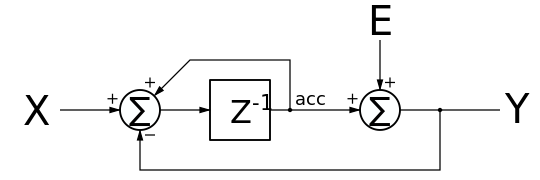
從這些等式中，可以找到訊號傳遞函式 (STF)

${\frac {Y(z)}{X(z)}}={\frac {1}{z}}$

以及噪聲傳遞函式 (NTF)

${\frac {Y(z)}{E(z)}}={\frac {z-1}{z}}$

STF 是一段時間的延遲，但 NTF 是一階高通函式。這表明由於切換而產生的調製噪聲佔據了更高的頻率。如果輸入訊號限制在低頻，則可以使用低通濾波器將訊號與噪聲分離。由於高通傳遞函式隨著頻率降低而以 20 dB/十倍頻程（或 6 dB/八度音程）降低，因此信噪比以相同的速率增加。將噪聲幅度在訊號頻帶內積分表明一階調製器每八度音程獲得 1.5 位的信噪比。這可以與 PCM 相比，PCM 每八度音程僅獲得 1 位的增益。

當輸入恆定時，一階調製器將提供迴圈模式。對於特定的輸入值，此模式可能變得非常長，這會導致調製訊號中出現低頻振鈴音。由於這些音調的頻率越來越低，因此越來越難以將它們與原始訊號分離。高階調製器顯示的重複模式更少，因此比一階調製器更受歡迎。

二階調製器

電路

二階 ΣΔ 調製器需要 2 個累加器。不同的拓撲結構是可能的。以下電路顯示了一個典型的二階電路。

這兩個係數允許與相應的噪聲整形特性一起控制數字到模擬的傳遞函式。

分析

同樣，比較器可以被誤差訊號的插入所取代

NTF 和 STF 可以從以下等式中找到

${\begin{array}{ccrcccccccccc}z\cdot {\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&=&{\begin{bmatrix}1&0\\1&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&+&{\begin{bmatrix}1\\0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}-c_{1}\\-c_{2}\end{bmatrix}}&\cdot &Y\\Y&=&{\begin{bmatrix}0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}1\end{bmatrix}}&\cdot &E\end{array}}$

可以改寫為

${\begin{array}{ccccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B} \cdot X&+&\mathbf {B_{y}} \cdot y\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X&+&\mathbf {D_{e}} \cdot E\end{array}}$

訊號傳遞函式

STF 是透過設定 $E=0$得到的：

${\begin{array}{ccccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B} \cdot X&+&\mathbf {B_{y}} \cdot (\mathbf {C} \cdot {\overrightarrow {acc}}+\mathbf {D} \cdot X)\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X\end{array}}$

這可以改寫為狀態空間表示:

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\cdot {\overrightarrow {acc}}&+&(\mathbf {B} +\mathbf {B_{y}} \cdot \mathbf {D_{e}} )\cdot X\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D} \cdot X\end{array}}$

狀態空間矩陣由調製矩陣 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 構成，如下所示：

${\begin{array}{l}A_{x}=(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\\B_{x}=(\mathbf {B} +\mathbf {B_{y}} \cdot \mathbf {D} )\\C_{x}=\mathbf {C} \\D_{x}=\mathbf {D} \end{array}}$

求解二階調製器的系統，得到：

${\frac {Y}{X}}={\frac {1}{z^{2}-(2-c_{2})z+(1+c_{1}-c_{2})}}$

噪聲傳遞函式

透過令 $X=0$，可以得到 NTF：

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&\mathbf {A} \cdot {\overrightarrow {acc}}&+&\mathbf {B_{y}} \cdot (\mathbf {C} \cdot {\overrightarrow {acc}}+\mathbf {D_{e}} \cdot E)\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D_{e}} \cdot E\end{array}}$

這可以改寫為狀態空間表示:

${\begin{array}{ccccc}z\cdot {\overrightarrow {acc}}&=&(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\cdot {\overrightarrow {acc}}&+&\mathbf {B_{y}} \cdot \mathbf {D_{e}} \cdot E\\Y&=&\mathbf {C} \cdot {\overrightarrow {acc}}&+&\mathbf {D_{e}} \cdot E\end{array}}$

狀態空間矩陣由調製矩陣 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 構成，如下所示：

${\begin{array}{l}A_{e}=(\mathbf {A} +\mathbf {B_{y}} \cdot \mathbf {C} )\\B_{e}=\mathbf {B_{y}} \cdot \mathbf {D_{e}} \\C_{e}=\mathbf {C} \\D_{e}=\mathbf {D_{e}} \end{array}}$

求解二階調製器的系統，得到：

${\frac {Y}{X}}={\frac {(z-1)^{2}}{z^{2}-(2-c_{2})z+(1+c_{1}-c_{2})}}$

評論

矩陣 $\mathbf {A} ,\mathbf {B} ,\mathbf {B_{y}} ,\mathbf {C} ,\mathbf {D} ,\mathbf {D_{e}}$ 包含了模擬和分析任何Σ-Δ調製器行為的所有資訊。從這些矩陣推匯出NTF和STF的狀態空間描述一般適用於任何Σ-Δ調製器。

矩陣 $\mathbf {A_{x}}$ 和 $\mathbf {A_{e}}$ 是相同的，這意味著STF和NTF具有相同的極點。STF只有極點，這導致了低通函式。NTF在 $Z=1$ 處有兩個極點，這給出了高通響應。這確保了訊號和噪聲是可分離的。

STF的直流增益為

${\frac {Y}{X}}(Z=1)={\frac {1}{c_{1}}}$

透過將輸入乘以$c_{1}$，可以實現 1 的 STF 直流增益。

設計

STF 的極點由下式給出

$p_{12}=(1-{\frac {c_{2}}{2}})\pm j{\sqrt {c_{1}-{\frac {c_{2}^{2}}{4}}}}$

這個方程允許任意地放置 STF 的極點。對於一對位於

$p_{12}=a\pm jb$

的極點，調製器係數為

${\begin{cases}{\begin{array}{ll}c_{1}&=(1-a)^{2}+b^{2}\\c_{2}&=2(1-a)\end{array}}\end{cases}}$

例如，一個截止頻率為取樣頻率 1/4 的全極點巴特沃斯 STF 給出的極點為

$p_{12}=0.375\pm j0.320$

和係數

${\begin{cases}{\begin{array}{ll}c_{1}&=0.493\\c_{2}&=1.250\end{array}}\end{cases}}$

一個接近貝塞爾 STF 的全極點 STF，其截止頻率約為取樣頻率的 1/4，給出的係數為

${\begin{cases}{\begin{array}{ll}c_{1}&=26/32\\c_{2}&=56/32\end{array}}\end{cases}}$

注意，使用係數$c_{1}=c_{2}=1$ 或 $c_{1}=c_{2}=1/2$ 的常規習慣會導致極點正好位於單位圓上，從穩定性的角度來看，這並不可取。

更高階拓撲

對於更高階調製器，存在不同的拓撲結構。

簡化積分器鏈路反饋 (SCIFB)

下圖顯示了一個簡化積分器鏈路反饋 (SCIFB) 調製器

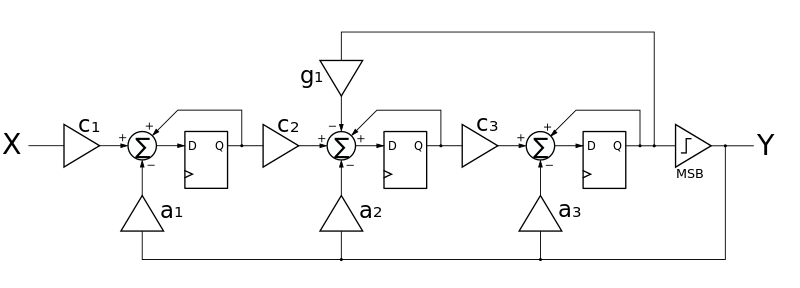SCIFB 調製器 - 階數 3

當係數$g_{1}$ 不為零時，這是一個具有區域性諧振器的結構。

對於這個結構，系統方程為

${\begin{array}{ccrcccccccccc}z\cdot {\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&=&{\begin{bmatrix}1&0&0\\c_{2}&1&-g_{1}\\0&c_{3}&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&+&{\begin{bmatrix}c_{1}\\0\\0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{bmatrix}}&\cdot &Y\\Y&=&{\begin{bmatrix}0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}acc_{1}\\acc_{2}\\acc_{3}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &X&+&{\begin{bmatrix}1\end{bmatrix}}&\cdot &E\end{array}}$

矩陣如下：

${\begin{array}{ccc}A&=&{\begin{bmatrix}1&0&0\\c_{2}&1&-g_{1}\\0&c_{3}&1\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}B&=&{\begin{bmatrix}c_{1}\\0\\0\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}B_{y}&=&{\begin{bmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}C&=&{\begin{bmatrix}0&0&1\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}D&=&{\begin{bmatrix}0\end{bmatrix}}\end{array}}$

${\begin{array}{ccc}D_{e}&=&{\begin{bmatrix}1\end{bmatrix}}\end{array}}$