訊號處理/濾波器設計

濾波器設計

濾波器設計通常從其頻率響應的規範開始。由此，必須選擇傳遞函式和濾波器結構。實際上，某些濾波器結構（例如二階段鏈）可適應任何濾波器函式，而基本梯形濾波器結構，其串聯支路僅包含電感，並聯支路僅包含電容，僅實現全極點低通傳遞函式。將傳遞函式對映到濾波器結構會給出模擬濾波器元素的元件值和數字濾波器的係數。

從理想濾波器開始，需要進行進一步的最佳化。

集中元件或係數值是理想值。集中元件值必須對映到現有元件的值。濾波器係數必須四捨五入到濾波器電路的數字表示支援的值。例如，選擇定點或浮點數字訊號處理器 (DSP) 將導致更粗略或更精細的係數值。

然後，必須考慮濾波器內部的訊號幅度。對於有源濾波器和數字濾波器，必須檢查內部訊號是否發生飽和或溢位。對於任何濾波器，訊號都不應變得太小，因為這會嚴重影響整個濾波器的信噪比。因此，基本上，濾波器設計過程不僅分析從輸入到輸出的傳遞函式，還分析從輸入到內部訊號的傳遞函式。

濾波器表示

濾波器可以用多種等效方式表示

顯然是透過其傳遞函式
透過傳遞函式的零點和極點，以及增益因子
透過濾波器的狀態空間表示

方法允許在一種表示形式之間切換。不同的表示形式對濾波器屬性有特定的啟示。傳遞函式，繪製為 $s=j\omega$ ，顯示了頻率如何被放大或衰減。零極點圖直接提供系統穩定性的資訊。狀態空間表示更深入地瞭解所選擇的濾波器結構，並允許分析濾波器內部某些訊號（狀態變數）的幅度。

傳遞函式

對於簡單的濾波器（如低通、高通、帶通或帶阻），選擇傳遞函式最常見的方法是選擇一個常用的濾波器函式：巴特沃斯、切比雪夫、橢圓、貝塞爾等等。

可實現的傳遞函式採用兩個多項式的商形式。

H(s)={\frac {num(s)}{den(s)}}

濾波器階數是兩個多項式中 $s$ （或對於取樣系統中的 $z$ ）的最大冪。

4階傳遞函式的形式為

H(s)={\frac {b_{4}s^{4}+b_{3}s^{3}+b_{2}s^{2}+b_{1}s+b_{0}}{a_{4}s^{4}+a_{3}s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}}

4階全極點傳遞函式的形式為

H(s)={\frac {1}{a_{4}s^{4}+a_{3}s^{3}+a_{2}s^{2}+a_{1}s+a_{0}}}

4階FIR傳遞函式的形式為

H(z)={\frac {b_{4}z^{4}+b_{3}z^{3}+b_{2}z^{2}+b_{1}z+b_{0}}{1}}=b_{4}z^{4}+b_{3}z^{3}+b_{2}z^{2}+b_{1}z+b_{0}

大多數濾波器型別試圖儘可能接近磚牆形狀，但其最佳化目標不同。對於這些型別，濾波器階數越高，函式越接近磚牆形狀。巴特沃斯濾波器透過具有最大平坦（無紋波）的傳遞函式來實現這一點。另一方面，貝塞爾濾波器的目標是最小化通帶中的群延遲變化。

這些傳遞函式是針對歸一化低通濾波器定義的。濾波器變換技術允許將低通函式變換為具有所需截止頻率的低通、高通、帶通或帶阻。

此外，這些函式代表時間連續系統，可透過拉普拉斯分析來理解。對於取樣系統（例如，開關電容或數字濾波器），還需要一個額外的步驟： $s$ 為基礎的傳遞函式需要轉換為 $z$ 為基礎的傳遞函式。

零點、極點和增益

零點是傳遞函式分子的根。極點是傳遞函式分母的根。增益是傳遞函式的直流值： $s=0$ 時的值。

由其零點 $z_{i}$ 、極點 $p_{i}$ 和增益 $k$ 給出的系統的傳遞函式為

H(s)=k\cdot {\frac {\prod _{i=1}^{M}(s-z_{i})}{\prod _{i=1}^{N}(s-p_{i})}}

一個穩定的線性時不變系統的所有極點都位於 $s$ 的左半平面（即，具有負實部）。

狀態空間表示

狀態空間表示將濾波器描述為一組微分方程

{\dot {\mathbf {x} }}(t)=A\cdot \mathbf {x} (t)+B\cdot u(t)

y(t)=C\cdot \mathbf {x} (t)+D\cdot u(t)

這裡，輸入是 $u(t)$ ，內部濾波器訊號是 $\mathbf {x} (t)$ ，輸出是 $y(t)$ 。這些方程的拉普拉斯變換由以下給出

s\cdot \mathbf {X} (s)=A\cdot \mathbf {X} (s)+B\cdot U(s)

Y(s)=C\cdot \mathbf {X} (s)+D\cdot U(s)

傳遞函式由下式給出：

H(s)={\frac {Y(s)}{U(s)}}=C(s\mathbf {I} -A)^{-1}B+D

$A$ 的特徵值是系統的極點。 $A$ 的特徵多項式是傳遞函式的分母。

例子

4 階歸一化巴特沃斯濾波器

例子

本示例將介紹 4 階歸一化巴特沃斯濾波器的不同表示形式。

與其他由多項式給出的濾波器函式相反，巴特沃斯濾波器最適合透過其極點的位置來描述。它是一個全極點函式：它沒有零點。

極點

歸一化的巴特沃斯濾波器在單位圓的左半平面部分具有等間距極點。對於 4 階濾波器，它們的取值為

{\begin{cases}p_{1},p_{1}^{*}=e^{\pm i(\pi /2+\pi /8)}\\p_{2},p_{2}^{*}=e^{\pm i(\pi /2+3\pi /8)}\end{cases}}or{\begin{cases}p_{1},p_{1}^{*}=-0.383\pm 0.924\cdot i\\p_{2},p_{2}^{*}=-0.924\pm 0.383\cdot i\end{cases}}

傳遞函式

因此，傳遞函式為

H(s)={\frac {1}{(s-p_{1})\cdot (s-p_{1}^{*})\cdot (s-p_{2})\cdot (s-p_{2}^{*})}}

H(s)={\frac {1}{(s^{2}-2\cdot re(p_{1})\cdot s+1)\cdot (s^{2}-2\cdot re(p_{2})\cdot s+1)}}

H(s)={\frac {1}{(s^{2}+0.765s+1)\cdot (s^{2}+1.848s+1)}}

H(s)={\frac {1}{s^{4}+2.61s^{3}+3.41s^{2}+2.61s+1}}

狀態空間表示

從傳遞函式中可以找到一個可能的狀態空間表示

Y(s)=U(s){\frac {1}{s^{4}+2.61s^{3}+3.41s^{2}+2.61s+1}}

s^{4}\cdot Y(s)+2.61s^{3}\cdot Y(s)+3.41s^{2}\cdot Y(s)+2.61s\cdot Y(s)+Y(s)=U(s)

s\cdot s^{3}\cdot Y(s)=-Y(s)-2.61s\cdot Y(s)-3.41s^{2}\cdot Y(s)-2.61s^{3}\cdot Y(s)+U(s)

寫作

{\begin{cases}X_{1}(s)=Y(s)\\X_{2}(s)=s\cdot Y(s)=s\cdot X_{1}(s)\\X_{3}(s)=s^{2}\cdot Y(s)=s\cdot X_{2}(s)\\X_{4}(s)=s^{3}\cdot Y(s)=s\cdot X_{3}(s)\\\end{cases}}

給出

s\cdot X_{4}(s)=-X_{1}(s)-2.61\cdot X_{2}(s)-3.41\cdot X_{3}(s)-2.61\cdot X_{4}(s)+U(s)

這可以被改寫成矩陣形式

{\begin{matrix}s\cdot {\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&=&{\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&0&1\\-1&-2.61&-3.41&-2.61\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\\0\\0\\1\end{bmatrix}}U\\Y&=&{\begin{bmatrix}1&0&0&0\end{bmatrix}}{\begin{bmatrix}X_{1}\\X_{2}\\X_{3}\\X_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}U\end{matrix}}

Octave 程式碼

以下Octave 程式碼提供相同的結果，並繪製了濾波器的幅頻響應

> order = 4;
> [z, p, g] = butter(order, 1, 's')
    z = []  (0x0)
    p = -0.38268 + 0.92388i
        -0.92388 + 0.38268i
        -0.92388 - 0.38268i
        -0.38268 - 0.92388i
    g =  1

> [b, a] = butter(order, 1, 's')
    b =  1
    a = 1.0000   2.6131   3.4142   2.6131   1.0000

> w = logspace(-1, 1, 100);
> while ( length(b) < length(a) )
>   b = [0, b];
> endwhile;
> Adb = 20*log10(abs(freqs(b, a, w)));
> figure(1);
> semilogx(w, Adb);
> grid;
   An amplitude response plot appears in a Gnuplot window

> [A, B, C, D] = tf2ss(b, a)
    A = 0.00000   1.00000   0.00000   0.00000
        0.00000   0.00000   1.00000   0.00000
        0.00000   0.00000   0.00000   1.00000
       -1.00000  -2.61313  -3.41421  -2.61313

    B = 0
        0
        0
        1

    C = 1   0   0   0

    D = 0

> eig(A)
    ans = -0.38268 + 0.92388i
          -0.38268 - 0.92388i
          -0.92388 + 0.38268i
          -0.92388 - 0.38268i

> poly(A)
    ans = 1.0000   2.6131   3.4142   2.6131   1.0000

模擬低通濾波器設計

例子

此示例介紹了從給定規格設計模擬低通濾波器的步驟。

規格

CCITT G712 輸入濾波器規格的簡化版本，只顯示低通部分，如側面的圖所示。

通帶頻率上限為 3 kHz，最大紋波為 0.125 dB。阻帶在 4 kHz 時需要衰減 14 dB，在 4.6 kHz 以上需要衰減 32 dB。

濾波器階數

第一步是評估常用濾波器函式所需的階數。由於對相位沒有要求，因此不需要考慮貝塞爾濾波器。

以下Octave 程式碼

fs = 40E3;
fPass = 3000;
rPass = 0.125;
fStop1 = 4000;
rStop1 = 14;
fStop2 = 4600;
rStop2 = 32;

order1 = buttord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = buttord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
buttOrder = max(order1, order2)

order1 = cheb1ord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = cheb1ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
cheb1Order = max(order1, order2)

order1 = cheb2ord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = cheb2ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
cheb2Order = max(order1, order2)

order1 = ellipord(fPass/(fs/2), fStop1/(fs/2), rPass, rStop1);
order2 = ellipord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
ellipticOrder = max(order1, order2)

disp('Required filter orders:');
printf("  Butterworth      : %2i\n", buttOrder)
printf("  Chebyshev type 1 : %2i\n", cheb1Order)
printf("  Chebyshev type 2 : %2i\n", cheb2Order)
printf("  Elliptic (Cauer) : %2i\n", ellipticOrder)

給出了結果

Required filter orders:
  Butterworth      : 13
  Chebyshev type 1 :  6
  Chebyshev type 2 :  6
  Elliptic (Cauer) :  4

巴特沃斯濾波器所需的硬體量大約是切比雪夫型別 1 的兩倍。切比雪夫型別 2 和橢圓濾波器具有切比雪夫型別 1 濾波器沒有的零點，因為它是一個全極點函式。因此，它們所需的硬體量也比切比雪夫型別 1 更多。

切比雪夫型別 1 將是為該濾波器選擇的候選者。

傳遞函式

Octave 自動執行頻率變換。幅頻響應使用

pointNb = 100;
wLog = logspace(2, 5, pointNb);
AdbMin = 40;

[order, wc] = cheb1ord(fPass/(fs/2), fStop2/(fs/2), rPass, rStop2);
order = order + 1;
wc = 1.03 * wc;
[num, den] = cheby1(order, rPass, (fs/2)*wc, 's');
while ( length(num) < length(den) )
  num = [0, num];
endwhile;
Adb = 20*log10(abs(freqs(num, den, wLog)));
Adb(Adb < -AdbMin) = -AdbMin;

figure(1);
semilogx(wLog, Adb);
grid;
hold on;
semilogx([wLog(1), fPass, fPass], -[rPass, rPass, AdbMin], 'r');
semilogx([fStop1, fStop1, fStop2, fStop2, wLog(length(wLog))], ...
        -[0     , rStop1, rStop1, rStop2, rStop2            ], 'r');
hold off;
xlabel('frequency [Hz]');
ylabel('amplitude [dB]');

獲得，如下面的圖所示

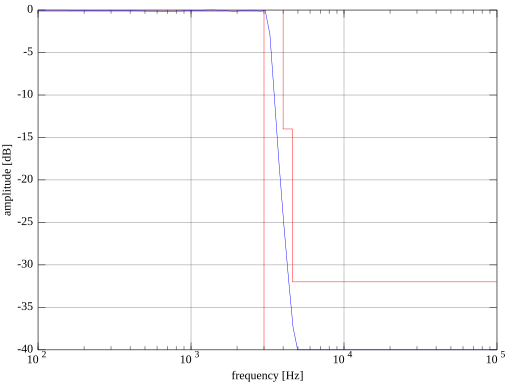
可能已經注意到，濾波器階數已提升至 7，截止頻率也略微提高，以便在通帶和阻帶側平衡與規格邊界的距離。

濾波器係數

顯然，濾波器係數取決於所選的濾波器結構。

對於二階段串聯，高階傳遞函式必須分解為二階傳遞函式的乘積

[zeroes, poles, gain] = cheby1(order, rPass, (fs/2)*wc, 's');
[SOS, G] = zp2sos(zeroes, poles, gain)

這將得到

SOS = 1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   2.0033e+03   3.0335e+06
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   1.3863e+03   7.0724e+06
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   4.9478e+02   1.0311e+07
      1.0000e+00   0.0000e+00   0.0000e+00   1.0000e+00   1.1118e+03  -0.0000e+00

G =  2.4594e+23 - 1.3998e+07i

SOS 矩陣行開頭的“1, 0, 0”表明它們都是全極點函式。

最後一行 SOS 矩陣，其第三位和最後一位的值為 0，表明它對應於一個一階段。事實上，7 階函式由 3 個二階段和一個一階段組成。

增益的虛部應該忽略：它肯定是一個定點計算的錯誤。增益的實部等於 SOS 矩陣行最後一個（非零）元素的乘積。

從這些係數中，可以找到狀態變數濾波器或薩倫-基電路的模擬元件值，兩者都是全極點型。這些係數也可以幾乎按原樣在規範雙二階濾波器中使用，但 $b_{1}=0$ 和 $b_{2}=0$ ，簡化了電路。