訊號處理/模擬濾波器

模擬濾波器

從歷史上看，電訊號處理始於類比電路。訊號分析和濾波器設計方法最初基於這類電路。後來出現了數字系統。第一個數字濾波器依賴於它們模擬父濾波器的技術。直到今天，一些數字濾波器仍然依賴於模擬濾波器的模擬，以便利用它們的一些有趣特性。

無源濾波器

集中元件濾波器

集中元件濾波器基於以下元件的頻率特性

• 電阻，R
• 電容，C
• 電感，L

它們的特性由下式給出

$U=R\cdot I$

$U={\frac {1}{sC}}\cdot I$

$U=sL\cdot I$

梯形濾波器

下圖顯示了一個四階全極點低通梯形濾波器

集中元件梯形濾波器四階

電路的整體外觀解釋了這個名字。

在圖中，源電阻和負載電阻是相同的。這對應於源到負載的最佳能量傳輸情況。在直流情況下，電感充當短路，電容充當開路。因此，輸出幅度將是輸入幅度的一半。

雙端梯形濾波器具有 優異的通帶靈敏度特性 。換句話說，L 或 C 元件值的給定變化會導致濾波器傳遞函式的相對變化小得多。因此，梯形濾波器已被廣泛用作模擬有源濾波器和數字濾波器的模型。

分佈元件濾波器

一個 分佈元件濾波器 是一種電子濾波器，其中電容、電感和電阻（電路的元件）不是像傳統濾波器那樣集中在離散（集中）元件中。在高頻，在微波區域，印刷電路板上的條帶充當阻抗，精心設計它們可以實現濾波器功能。

有源濾波器

有源濾波器是使用放大器件（如運算放大器）的模擬濾波器。它們允許使用電阻和電容實現濾波器功能，使設計人員不必使用電感。

典型濾波器

實現有源濾波器的首次嘗試是設計一個電路來實現傳遞函式，其中 R 和 C 元件值組合對應於傳遞函式的分子和分母系數：典型濾波器。然而，這種電路顯示出對元件值的敏感性非常高：R 或 C 元件值的微小變化會對傳遞函式產生很大的影響。

出於這個原因，有源濾波器的設計已從典型濾波器轉向其他結構，例如二階段串聯或交錯濾波器。

二階段串聯

一個二階段，通常稱為雙二階，實現一個二階傳遞函式。濾波器的傳遞函式可以分解為傳遞函式的乘積，每個傳遞函式與一對極點和可能的一對零點相關聯。

具有相同數量複共軛零點 $z_{i}$ 和 $z_{i}^{*}$，以及極點 $p_{i}$ 和 $p_{i}^{*}$，以及增益 $k$ 的系統的傳遞函式為

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {(s-z_{i})(s-z_{i}^{*})}{(s-p_{i})(s-p_{i}^{*})}}$

這是切比雪夫二型和橢圓 濾波器函式 的情況。

寫

$D_{i}(s)=(s-p_{i})(s-p_{i}^{*})=s^{2}-2Re(p_{i})s+abs(p_{i})^{2}=s^{2}+a_{1i}s+a_{0i}$

表明 $s$ 的分母多項式函式具有實係數。分子也可以這樣說。由此，傳遞函式可以改寫為

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {s^{2}+b_{1i}s+b_{0i}}{s^{2}+a_{1i}s+a_{0i}}}$

如果傳遞函式的階數為奇數，則需要在鏈中新增一個一階部分。該部分與實極點 $p_{r}$ 和實零點 $z_{r}$ 相關聯，如果存在的話。傳遞函式變為

$H(s)=k\cdot {\frac {s-z_{r}}{s-p_{r}}}\cdot \prod _{i=1}^{{N-1}/2}{\frac {s^{2}+b_{1i}s+b_{0i}}{s^{2}+a_{1i}s+a_{0i}}}$

全極點偶數階傳遞函式的形式為

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {1}{(s-p_{i})(s-p_{i}^{*})}}=k\cdot \prod _{i=1}^{N/2}{\frac {1}{s^{2}+a_{1i}s+a_{0i}}}$

這種情況適用於巴特沃斯、切比雪夫一型和貝塞爾 濾波器函式。

一個全極點奇數階傳遞函式的形式為

$H(s)=k\cdot {\frac {1}{s-p_{r}}}\cdot \prod _{i=1}^{{N-1}/2}{\frac {1}{s^{2}+a_{1i}s+a_{0i}}}$

狀態變數濾波器

狀態變數濾波器 具有兩個積分器的拓撲結構，其輸出對應於與傳遞函式相關的狀態空間變數。

以下電路是由 Kerwin、Huelsman 和 Newcomb 提出的

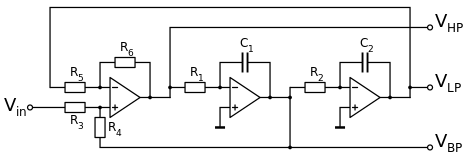
以下電路被稱為 Tow-Thomas 電路

透過 Kerwin-Huelsman-Newcomb 和 Tow-Thomas，都可以透過對所有運算放大器輸出進行加權求和來獲得更通用的傳遞函式。

某些二階 規範結構 直接使用傳遞函式的係數作為放大器增益。

薩倫-基電路

薩倫-基 拓撲結構使用運算放大器驅動輸出，並使用 RC 元件設定傳遞函式。由於運算放大器的驅動能力，薩倫-基電路很容易級聯形成更高階的濾波器。

以下電路顯示了一個薩倫-基低通濾波器電路

跳躍濾波器

濾波器結構

跳躍濾波器 基於對 無源梯形濾波器 的模擬。這種選擇的動機是繼承原始電路優異的通帶靈敏度特性。

以以下 4 階全極點低通梯形濾波器為例，

集中元件梯形濾波器四階

可以寫出以下方程

${\begin{cases}sC_{1}\cdot U_{1}={\frac {1}{R}}\cdot (U_{in}-U_{1})-I_{2}\\sL_{2}\cdot I_{2}=U_{1}-U_{3}\\sC_{3}\cdot U_{3}=I_{2}-I_{4}\\sL_{4}\cdot I_{4}=U_{3}-R\cdot I_{4}\\U_{out}=R\cdot I_{4}\end{cases}}$

重寫這些方程得到

${\begin{cases}U_{1}={\frac {1}{sRC_{1}}}(U_{in}-U_{1}-RI_{2})\\RI_{2}={\frac {R}{sL_{2}}}(U_{1}-U_{3})\\U_{3}={\frac {1}{sRC_{3}}}(RI_{2}-RI_{4})\\RI_{4}={\frac {R}{sL_{4}}}(U_{3}-RI_{4})\\U_{out}=RI_{4}\end{cases}}$

這個新的方程組表明，該濾波器可以用 4 個積分器鏈實現，

• 狀態變數 形如 $w_{i}=U_{i}$ 或 $w_{i}=RI_{i}$
• 時間常數 形如 $t_{i}=RC_{i}$ 或 $t_{i}={\frac {L_{i}}{R}}$

得到的電路是一個積分器鏈，每個積分器的輸出都被反饋到前一個積分器的輸入。因此稱為跳躍。

傳遞函式

描述濾波器的方程組可以使用狀態空間表示重寫為

${\begin{array}{ccrcccccc}s\cdot {\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&=&{\begin{bmatrix}-{\frac {1}{t_{1}}}&-{\frac {1}{t_{1}}}&0&0\\{\frac {1}{t_{2}}}&0&-{\frac {1}{t_{2}}}&0\\0&{\frac {1}{t_{3}}}&0&-{\frac {1}{t_{3}}}\\0&0&{\frac {1}{t_{4}}}&-{\frac {1}{t_{4}}}\end{bmatrix}}&\cdot &{\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&+&{\begin{bmatrix}{\frac {1}{t_{1}}}\\0\\0\\0\end{bmatrix}}&\cdot &U_{in}\\U_{out}&=&{\begin{bmatrix}0&0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &U_{in}\end{array}}$

從這個方程組中，我們可以寫出 A、B、C、D 矩陣為

$A={\begin{bmatrix}-{\frac {1}{t_{1}}}&-{\frac {1}{t_{1}}}&0&0\\{\frac {1}{t_{2}}}&0&-{\frac {1}{t_{2}}}&0\\0&{\frac {1}{t_{3}}}&0&-{\frac {1}{t_{3}}}\\0&0&{\frac {1}{t_{4}}}&-{\frac {1}{t_{4}}}\end{bmatrix}}$

$B={\begin{bmatrix}{\frac {1}{t_{1}}}\\0\\0\\0\end{bmatrix}}$

$C={\begin{bmatrix}0&0&0&1\end{bmatrix}}$

$D={\begin{bmatrix}0\end{bmatrix}}$

透過這種表示方式，訊號處理工具例如Octave 或Matlab 可以用來繪製濾波器的頻率響應或檢查其零點和極點。

開關電容濾波器

開關電容濾波器是模擬取樣器件。對電容器進行充放電可以產生類似於電阻的阻抗。這樣，模擬有源濾波器的RC時間常數就變成了兩個電容之比的比例因子。這種型別的電路對於積體電路設計非常有用，因為在同一個矽晶片的不同區域，R和C元件的值可能會有很大差異，而兩個電容之比在同一個區域內的偏差卻非常小。