電子學/直流電壓和電流

電子學 | 前言 | 基礎電子學 | 複雜電子學 | 電力 | 機器 | 電子學歷史 | 附錄 | 編輯

歐姆定律

歐姆定律描述了電壓、電流和電阻之間的關係。電壓和電流與電位差成正比，與電路的電阻成反比。

$V=I\cdot R$

電壓 (V) 的單位是伏特 (V)；電流 (I) 的單位是安培 (A)；電阻 (R) 的單位是歐姆 (Ω)。

在這個例子中，流經電路中任何點的電流 I 等於電壓 V 除以電阻 R。

在這個例子中，電阻兩端的電壓 V 等於提供的電流 I 乘以電阻 R。

如果已知兩個值 (V、I 或 R)，則可以使用此公式計算出另一個值。

任何更復雜的電路都有一個等效電阻，我們可以用它來計算電壓源的電流消耗。等效電阻是根據所有電阻都串聯或並聯的事實得出的。類似地，如果電路只有一個電流源，則可以使用等效電阻來計算電流源兩端的壓降。

基爾霍夫電壓定律

基爾霍夫電壓定律 (KVL)

電路中任何從同一地點開始並結束的迴路中，電壓降的總和必須為零。

電壓作為物理量

1. 電壓是兩個帶電物體之間的電位差。
2. 電位可以在串聯中加在一起或減去，以形成更大的電位或更小的電位，就像電池中通常做的那樣。
3. 正電荷從高電位區域流向低電位區域。
4. 電路的所有元件都有電阻，電阻充當電位降。

基爾霍夫電流定律

基爾霍夫電流定律 (KCL)

進入節點的所有電流的總和必須等於離開節點的所有電流的總和。

KCL示例

-I₁ + I₂ + I₃ = 0 ↔ I₁ = I₂ + I₃

I₁ - I₂ - I₃ - I₄ = 0 ↔ I₂ + I₃ + I₄ = I₁

$I_{1}=I_{2}+I_{3}+\cdots +I_{n}\,\!$

這裡有更多關於基爾霍夫定律的資訊，可以整合到此處。

KVL和KCL的結果

電壓分配器

如果兩個電路元件串聯，則每個元件都會產生電壓降，但流過兩個元件的電流必須相同。鏈條中任何點的電壓都會根據電阻進行分配。一個簡單的電路，其中兩個（或更多）電阻串聯連線到一個電源，被稱為電壓分配器。

圖 A：電壓分配器電路。

考慮圖 A 中的電路。根據 KVL，電壓$V_{in}$ 會降落在電阻$R_{1}$ 和 $R_{2}$ 上。如果電流 i 流過這兩個串聯電阻，則根據歐姆定律。

$i={\frac {V_{in}}{R_{1}+R_{2}}}$.

所以

$V_{out}=iR_{2}\,\!$

因此

$V_{out}={\frac {V_{in}R_{2}}{R_{1}+R_{2}}}$

類似地，如果 $V_{R1}$ 是跨越 $R_{1}$ 的電壓，那麼

$V_{R1}={\frac {V_{in}R_{1}}{R_{1}+R_{2}}}$

一般來說，對於 n 個串聯電阻，跨越其中一個電阻，比如 $R_{i}$ 的電壓是

$V_{Ri}={\frac {V_{in}R_{i}}{R_{eq}}}$

其中

$R_{eq}=R_{1}+\cdots +R_{n}$

分壓器作為參考

顯然，分壓器可以用作參考。如果你有一個 9 伏電池，你需要 4.5 伏，那麼可以串聯兩個相等值的電阻，然後從第二個電阻和地之間獲取參考電壓。當然，還有一些其他的問題需要注意，第一個問題是電流消耗和源阻抗的影響。很明顯，如果源阻抗為 50 歐姆，那麼串聯兩個 100 歐姆電阻就是一個糟糕的選擇。在這種情況下，電流消耗將為 0.036 mA，如果電池的額定容量為 200 毫安時，這個電流消耗相當大。源阻抗也會導致更煩人的負載問題，在這種情況下，參考電壓將為 ${\frac {9(100)}{250}}=3.6{\mbox{ V}}$。因此，為了減少電流消耗和負載的影響，將電阻的值提高到至少 1 k$\Omega$ 是一個不錯的選擇。分壓器參考的另一個問題是，如果我們將一個 100 Ω 電阻與一個 10 kΩ 電阻並聯，則參考電壓不能載入。當分壓器由兩個 10 kΩ 電阻組成時，參考電阻的阻抗就會下降到接近 100 Ω。很明顯，這會導致一個很差的參考電壓。如果使用 10 MΩ 電阻作為參考電阻，其阻抗仍然會下降到大約 10 kΩ，但可能仍然會更低。容差的影響也是一個問題；如果電阻的額定值為 5%，那麼 10 kΩ 電阻的阻抗可以變化 ±500 Ω。這意味著這種型別的參考電壓會更不精確。

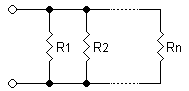
分流器

如果兩個元件並聯，則它們兩端的電壓必須相同，但電流會根據電阻的大小進行分配。一個簡單的電路，包含兩個（或更多）並聯的電阻和一個電源，被稱為 分流器。

圖 B：並聯電阻。

如果在圖 B 中，一個電壓 V 跨越電阻，並且此時只有 $R_{1}$ 和 $R_{2}$，那麼流過電路的電流，在電流分配之前，i 符合歐姆定律。

$i={\frac {V}{R_{eq}}}$

並聯電阻的等效電阻計算公式為

$i={\frac {V(R_{1}+R_{2})}{R_{1}R_{2}}}$ (1)

根據歐姆定律，透過 $R_{1}$ 的電流為

$i_{1}={\frac {V}{R_{1}}}$ (2)

將公式 (2) 除以 (1)

$i_{1}={\frac {iR_{2}}{R_{2}+R_{1}}}$

類似地

$i_{2}={\frac {iR_{1}}{R_{2}+R_{1}}}$

一般情況下，對於 n 個電阻器，電流 $i_{x}$ 為

$i_{x}={\frac {iR_{1}R_{2}\cdots R_{n}}{(R_{2}\cdots R_{n}+\cdots +R_{1}\cdots R_{n-1})R_{x}}}$

或者更簡單的

${\frac {i_{x}}{i}}={\frac {R_{eq}}{R_{x}}}$

其中

$R_{eq}={\frac {R_{1}\cdots R_{n}}{R_{2}\cdots R_{n}+\cdots +R_{1}\cdots R_{n-1}}}$