電子學/電感器/網路

串聯

考慮如上所示的n個串聯電感器。整個裝置上的電壓（即兩個端子上的電壓）必須等於各個電感器上的電壓之和。

$v_{tot}=v_{1}+v_{2}+\cdots +v_{n}.$

根據我們對電感的定義，電壓等於電感乘以電流的變化率，我們得到

$v_{tot}=L_{1}{\frac {di_{1}}{dt}}+L_{2}{\frac {di_{2}}{dt}}+\cdots +L_{n}{\frac {di_{n}}{dt}},$

其中i₁是元件1中的電流，依此類推。由於串聯電路中每個元件的電流必須始終相同（根據基爾霍夫電流定律），我們可以看到

$v_{tot}=L_{1}{\frac {di}{dt}}+L_{2}{\frac {di}{dt}}+\cdots +L_{n}{\frac {di}{dt}},$

其中i是網路中的電流。分解後，我們得到

$v_{tot}=\left(L_{1}+L_{2}+\cdots +L_{n}\right){\frac {di}{dt}}$.

如果我們現在將串聯中的所有元件稱為一個等效電感L_eq，我們會看到

$v_{tot}=L_{eq}{\frac {di}{dt}}.$

因此，

$L_{eq}=L_{1}+L_{2}+\cdots +L_{n}$

這意味著串聯時，總電感只是所有組成電感之和。

並聯

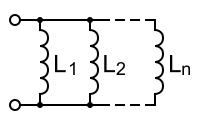
當電感器並聯時，每個電感器上的電壓相同，即網路端子上存在的電壓。這可以簡稱為v。現在，描述等效電感L_eq的方程式為

$v=L_{eq}{\frac {di_{eq}}{dt}},$

其中i_eq是流經網路的電流。

根據基爾霍夫電流定律，我們有

$i_{eq}=i_{1}+i_{2}+\cdots +i_{n}$

關於時間求導得到

${\frac {di_{eq}}{dt}}={\frac {di_{1}}{dt}}+{\frac {di_{2}}{dt}}+\cdots +{\frac {di_{n}}{dt}}$

現在，透過重新排列描述第i個元件中電感的通用方程式，我們可以為上述每個項獲得

${\frac {di_{i}}{dt}}={\frac {v}{L_{i}}}$

代入之前的方程式，我們得到

${\frac {di_{eq}}{dt}}={\frac {v}{L_{1}}}+{\frac {v}{L_{2}}}+\cdots +{\frac {v}{L_{n}}}$

因式分解後，

${\frac {di_{eq}}{dt}}=v\left({\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}\right)$

重新排列，得到

$v={\frac {\frac {di_{eq}}{dt}}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}$

$v={\frac {1}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}{\frac {di_{eq}}{dt}}$

因此，

$L_{eq}={\frac {1}{{\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}}$

${\frac {1}{L_{eq}}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}$

這與電阻組合規則相同。