電子學/運算放大器/線性配置

反相運算放大器

反相運算放大器的閉環增益“mon then”為

$R_{1}=R_{in}$

$A_{f}=-{\frac {R_{f}}{R_{1}}}$ (i)

此配置的輸入阻抗為 $Z_{in}=R_{in}$ (因為 $V_{-}$ 是虛擬地，理想情況下沒有電流流入運算放大器）。

為了得到公式 (i)，我們用 $V_{in}$，$R_{1}$ 和運算放大器的輸入構建一個 KVL 迴圈。這將得到

$V_{in}=i_{in}R_{1}+v_{d}\,$

其中 $v_{d}$ 是 $v_{+}-v_{-}$，即非反相輸入和反相輸入之間的電壓。但對於理想運算放大器，$v_{d}$ 近似為零。$v_{d}$ 為零是因為輸入阻抗為無窮大，這意味著透過阻抗的電流必須為零，根據歐姆定律。零電流意味著阻抗上沒有壓降。這將得到

$i_{in}={\frac {V_{in}}{R_{1}}}$ (5)

使用這個想法。

$i_{f}={\frac {V_{out}}{R_{f}}}$(6)

如果我們在反相輸入處進行 KCL，那麼

$i_{in}=i_{d}-i_{f}\,$

對於理想運放，由於其輸入阻抗無窮大，所以沒有輸入電流。因此可以使用公式 5 和 6。

$-{\frac {V_{in}}{R_{1}}}={\frac {V_{out}}{R_{f}}}$

因為

$A_{f}={\frac {V_{out}}{V_{in}}}=-{\frac {R_{f}}{R_{1}}}$

---

示例 1

設計一個反向放大器，將 100mV 的訊號放大到 1V 的訊號。假設：無源阻抗。

解決方案

步驟 1：計算所需的增益。

$|A_{f}|={\frac {1}{0.1}}=10$

步驟 2：選擇 $R_{f}$ 的值。

選擇 $R_{f}=100k\Omega$.

步驟 3：使用公式 (i) 計算 $R_{1}$ 的所需值。

$R_{1}={\frac {100k}{10}}=10k\Omega$

示例 2

設計一個反向放大器，將 10mV 的訊號放大到 1V 的訊號。訊號具有 100 $\Omega$ 的源阻抗。放大器不能反轉訊號。

解決方案

由於電壓不能反轉，因此必須有偶數個級。為了簡單起見，我們選擇兩個級。假設一個理想運放。

步驟 1：計算所需的增益。

$A_{f_{tot}}={\frac {1}{0.01}}=100$

步驟 2：選擇每個級所需的增益。

兩級的增益都將為 10。但在第一級，我們必須考慮負載的影響。

步驟 3：選擇輸入阻抗的值，即選擇 $R_{1}$.

選擇 $10k\Omega$。現在我們可以透過分壓器計算運放的輸入電壓。

$V_{in}={\frac {R_{1}V_{s}}{R_{1}+R_{s}}}={\frac {(10k)(10mV)}{10k+100}}=9.9mV$

我們希望這一級的輸出為 100mV。

$A_{f1}={\frac {100}{9.9}}=10.1$

步驟 4：使用 $A_{f1}$ 計算 $R_{f1}$.

使用公式 (i) $R_{f}=A_{f1}R_{1}=101k\Omega$

步驟 5：為第二級選擇一個 $R_{f}$。

選擇 100k。

步驟 6：使用公式 (i) 計算 $R_{1}$。

$R_{1}=10k\Omega$

---

非反相運算放大器

一個以非反相放大器配置連線的運算放大器

非反相運算放大器的閉環增益為

$A_{f}=1+{\frac {R_{2}}{R_{1}}}$ (ii)

這種配置的輸入阻抗為 Zin = ∞（實際上，運算放大器本身的輸入阻抗為 1 MΩ 至 10T Ω）。

理想運算放大器推導

對運算放大器和 R₁ 的輸入進行 KVL 分析。

$V_{in}=v_{d}+V_{R1}\,$

但 $v_{d}$ 為零，因為運算放大器是理想的。因此

$V_{in}=V_{R1}\,$(3)

根據分壓器規則

$V_{R1}={\frac {V_{out}R_{1}}{R_{1}+R_{2}}}$(4)

將公式 4 代入 3。

$V_{in}={\frac {V_{out}R_{1}}{R_{1}+R_{2}}}$

因此

$A_{f}={\frac {V_{out}}{V_{in}}}=1+{\frac {R_{2}}{R_{1}}}$

反饋分析推導

如果輸出連線到反相輸入，在透過一個分壓器 K = R₁ / (R₁ + R₂) 進行縮放後，那麼

V₊ = V_in

V₋ = K V_out

V_out = G(V_in − K V_out)

求解 V_out / V_in，我們可以看到結果是一個增益為

V_out / V_in = G / (1 + G K)

如果 G 很大，V_out / V_in 將接近 1 / K，等於 1 + (R2 / R1)。

這種負反饋連線是運算放大器最典型的用法，但還有許多不同的配置方式，使其成為所有電子構建模組中最通用的之一。

當以負反饋配置連線時，運算放大器將傾向於輸出使輸入電壓相等的任何電壓。這以及高輸入阻抗有時被稱為運算放大器設計的兩條“黃金法則”（用於使用反饋的電路）

1. 沒有電流流入輸入端
2. 輸入電壓彼此相等

唯一的例外是如果所需的電壓大於運算放大器的電源電壓，在這種情況下，輸出訊號將停止在電源軌附近，V_S+ 或 V_S−。

---

示例 3

設計一個非反相放大器，將 100mV 訊號放大為 1V 訊號。假設：沒有源阻抗。

步驟 1：計算所需的增益。

$A_{f}={\frac {1}{0.1}}=10$

步驟 2：選擇一個 $R_{2}$ 值。

選擇$R_{2}=90k\Omega$。

步驟 3：使用方程式 (ii) 計算出所需的$R_{1}$ 值。

$10=1+{\frac {90k}{R_{1}}}$

$R_{1}={\frac {90k}{9}}=10k\Omega$

---

示例 4（快速設計步驟）

我想要放大增益為 8 的訊號 A。我們想要至少 -3 到 +3 V 的輸出擺幅。

我們有一個 5V 和 -5V 的電源可用，所以我們可以使用它。

1. 訊號 A 的增益為 8。

2. 地增益 = 1 - (8) = -7。

3. 反饋電阻值：Rf = 100 千歐。

4. 每個輸入的電阻值

• R_A = 100 kΩ / 8 = 12.5 kΩ
• R_地 = 100 kΩ / |-7| = 14.3 kΩ

由於訊號 A 的增益為正，將其電阻連線到 V₊。由於地增益為負，將其電阻連線到 V₋。

---

示例 5

設計一個兩級非反相放大器，將 10mV 訊號放大到 1V 訊號。訊號的源阻抗為 100 Ω。

解決方案 假設一個理想運算放大器。由於該配置具有運算放大器本身的輸入阻抗。我們不必擔心載入，因為輸入阻抗是無限的。

步驟 1：計算所需的增益。

$A_{f}={\frac {1}{0.01}}=100$

步驟 2：選擇每個級的增益。

對兩個級都選擇 10。

步驟 3：選擇$R_{2}$ 電阻在兩個級中的值。

對兩個級都選擇 90kΩ。

步驟 4：計算出$R_{1}$ 的值。

使用方程式 (ii) $R_{1}=10k\Omega$。

---

電壓跟隨器

電壓跟隨器

此配置也被稱為單位增益緩衝器。因為它可以用來抵消源載入的影響。它提供的輸入阻抗甚至高於普通的非反相放大器，因為增益降低了該輸入阻抗。增益由方程式 (ii) 給出。但 R_2 短路，R_1 開路。

$A_{f}=1+{\frac {R_{2}}{R_{1}}}=1+{\frac {0}{\infty }}=1$

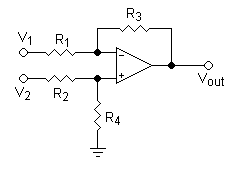差分放大器

差分放大器

此配置只是同時連線的反相和非反相配置。電阻 R₂ 和 R₄ 是一個分壓器。考慮 R₄ 開路，R₂ 短路的情況。現在，從方程式 (i) 和 (ii) 我們知道，V₁ 的增益是

$A_{f1}=-{\frac {R_{3}}{R_{1}}}$

而 V₂ 的增益是

$A_{f2}=1+{\frac {R_{3}}{R_{1}}}$

現在如果我們將 $A_{f1}$ 設定為 -10，那麼 $A_{f2}$ 將變為 11。這意味著 V_out 將是

$V_{out}=V_{1}A_{f1}+V_{2}A_{f2}=V_{2}(11)-(10)V_{1}$

這意味著如果 $V_{1}=V_{2}$，那麼 V_out 將是 V₂。這對大多數情況來說沒什麼用，因為數學上我們希望答案為零。但是，如果我們使非反相輸入的電壓等於 10/11，那麼當電壓相等時，我們將得到零。

當 R₄ 和 R₂ 連線時，V₂ 的增益為

$A_{f2}={\frac {(1+{\frac {R_{3}}{R_{1}}})R_{4}}{R_{4}+R_{2}}}$ (x)

V₁ 的增益為

$A_{f1}=-{\frac {R_{3}}{R_{1}}}$ (y)

如果我們想要 $A_{f2}=|A_{f1}|$

${\frac {R_{3}}{R_{1}}}={\frac {(R_{1}+R_{3})R_{4}}{(R_{4}+R_{2})R_{1}}}$

我們只需設定 $R_{4}=R_{3}$ 和 $R_{2}=R_{1}$.

這種配置具有較低的輸入阻抗。V₁ 看到的輸入阻抗是 R₁，就像反相放大器中一樣。V₂ 看到的輸入阻抗是 R₂ + R₄。

---

示例 6（快速設計步驟）

我們通常希望將一個訊號 A 從另一個訊號 B 中減去，並將差值放大 10 倍。我們希望輸出擺幅至少為 -6V 到 +6V。另外，出於安全考慮，A 和 B 每個都有 8 kΩ 的源阻抗。

我們的 5V 和 -5V 電源供應不足，因此我們選擇 +12V 和 -12V 電源供應。

1.

• B 的增益為 +10。
• A 的增益為 -10。

2. 地增益 = 1 - (+10 + -10) = +1。

3. 反饋電阻值：Rf = 100 千歐。

4. 每個輸入的電阻值

• R_A = 100 kΩ / |-10| = 10 kΩ
• R_B = 100 kΩ / |+10| = 10 kΩ
• R_ground = 100 kΩ / |+1| = 100 kΩ

因此，我們將 100 kΩ 的 Rf 從 V_out 連線到 V₋，另一個 100 kΩ 從地連線到 V₊。然後我們將 2 kΩ 從 R_A 連線到 V₋，另一個 2 kΩ 從 R_B 連線到 V₊。

如果輸入具有源阻抗，則源阻抗是電路的一部分。8 kΩ 的源阻抗加上我們新增的 2 kΩ 物理電阻，使我們得到理想電壓源和運算放大器輸入之間的總阻抗為 10 kΩ。

---

反相求和放大器

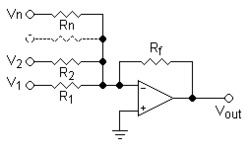反相求和放大器

這僅僅是一個具有額外輸入的反相放大器。分析幾乎相同，但我們有許多電流等於反饋電流。如果我們在反相輸入處進行 KCL。

$i_{n}+\cdots +i_{2}+i_{1}=-i_{f}$

電流值可以透過歐姆定律確定，使用理想運算放大器的 v_d 為零的事實。

${\frac {V_{n}}{R_{n}}}+\cdots +{\frac {V_{2}}{R_{2}}}+{\frac {V_{1}}{R_{1}}}=-{\frac {V_{out}}{R_{f}}}$

如果 $R_{n}=\cdots =R_{2}=R_{1}$ 那麼

${\frac {1}{R_{1}}}(V_{n}+\cdots +V_{2}+V_{1})=-{\frac {V_{out}}{R_{f}}}$

$A_{f}=-{\frac {V_{out}}{V_{sum}}}=-{\frac {R_{f}}{R_{1}}}$

就像反向放大器一樣。

注意：還有一種使用同向放大器配置的求和放大器。該配置稍微複雜一些，難以使用，因為它需要理解疊加原理。

理想積分器

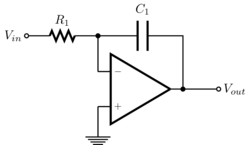積分放大器

該配置是一個反向放大器，其反饋電阻是一個電容。推導過程相同。

$i=-i_{f}$

${\frac {V_{in}}{R}}=-C{\frac {\;dV_{out}}{\;dt}}$

${\frac {V_{in}}{RC}}=-{\frac {\;dV_{out}}{\;dt}}$

將兩邊關於

$V_{out}=\int _{t_{0}}^{0}-{\frac {V_{in}}{RC}}\,dt+V_{initial}$

實際上，一個電阻通常與反饋電容並聯。這意味著在非常低的頻率下沒有無限增益，這使得實際積分器更加穩定。

理想微分器

該配置是一個反向放大器，其電容作為第一個電阻，因此推導過程與之前相同。

$i=-i_{f}\,$

$C{\frac {\;dV_{in}}{\;dt}}=-{\frac {V_{out}}{R}}$

$V_{out}=-RC{\frac {\;dV_{in}}{\;dt}}$

這種配置由於幾個原因不穩定。較高頻率的輸入將具有更高的導數。這意味著電路充當低通濾波器，但更重要的是，這意味著如果將高頻訊號輸入到微分器，它將直接飽和。這也是透過增益看到的。

$A_{f}=-{\frac {R}{1/j\omega C}}$

這意味著高頻意味著高增益，從而導致飽和。

在實際應用中，電阻器通常與電容器串聯連線。